Прямаяобщегоположения Прямые частного положения
l II П k and l ^ П k Прямыеуровня Проецирующие прямые
l II П k l ^ П k
Прямые общего положения l II П k and l ^ П k
Прямые общего положения не параллельны и не перпендикулярны плоскостям проекций
Прямые частного положения
Прямые уровня
Линии, параллельные одной из плоскостей проекций называются линиями уровня
Горизонталь h || П 1Þ h2 || x12
Угол φ наклонагоризонталикплоскости П2 проецируется на П1 в натуральную величину.
Фронталь f || П2Þ f1 || x12
Угол φ наклонафронталикплоскости П1 проецируется на П2 в натуральную величину.
Профильная прямаяp || П3
П3 – профильная плоскость проекций.
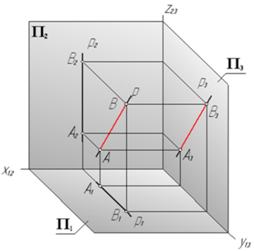
расстояние| AA 1 | - высота точки A
расстояние| AA 2 | - глубина точки A
расстояние| AA 3 | - ширина точкиt A
углы α и β наклонапрофильнойпрямой к плоскостям П2 и П1 проецируются на плоскость П3 в натуральную величину.
Проецирующие прямые
Прямые перпендикулярные к одной из плоскостей проекций называются проецирующими
Горизонтально-проецирующаяпрямая g перпендикулярна к горизонтальной плоскости проекций П1
g ^ П1
Горизонтальная проекция этой прямой g есть точка.
Точки A и B являются конкурирующими по отношению к П1
Фронтально-проецирующаяпрямая j перпендикулярна к фронтальной плоскости П2
j ^ П2
Фронтальная проекция этой прямой j есть точка
Точки A и B конкурирующие относительно плоскости П2
Точки, лежащие на одной проецирующей прямой, называются конкурирующими точками
Взаимное положениеие прямых
Пересекающиеся прямые
Если прямые пересекаются в пространстве, то проекции точек пересечения их проекций лежат на одной линии связи.
m ∩ n = D Þ mk ∩ nk = Dk
m 1 ∩ n 1 = D 1 m 2 ∩ n 2 = D 2 D 1 D 2 ^ x 12
Параллельные прямые
Если прямые в пространстве параллельны, то их одноименные проекции параллельны
m || n Þ mk || nk
m 1 || n 1
m 2 || n 2
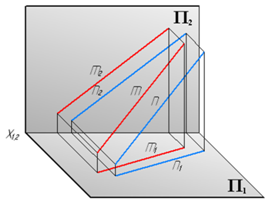
Скрещивающиеся прямые
Скрещивающиесяпрямыенеимеютобщейточки, точки пересечения их горизонтальных и фронтальных проекций не лежат на одной линии связи.
m × n Þ m || n Ù m ∩ n
Плоскость
Плоскость – это простейшая поверхность
Способы задания плоскости
Только одна плоскость проходит через три точки
На чертеже лоскость может быть задана проекциями элементов, определяющих ее в пространстве
Положение плоскости относительно плоскостей проекций
Положение плоскости относительно плоскостей проекций
ПлоскостьобщегоположенияПлоскости частного положения
Проецирующие плоскостиПлоскости уровня
U || П k Ù U ^ П k Т ^ П k Г || П k
