Проекция точек, расположенных в разных четвертях пространства

Метод проекцирования

Основной метод для построения изображений на плоскости является метод проецирования

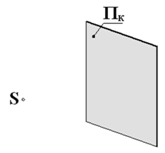Аппарат проецирования:

П _k – _________________________________________________

S – _________________________________________________

 

А – ___________________________________________

SA – _________________________________________

Метод проекцирования: _____________________________________________

А _k – ____________________________________________________________

 

Виды проецирования

Центральное проецирование

 

S (центр проецирования) – действительная точка.

Проецирующие лучи проходят через центр проецирования

S A ∩ S B ∩ S C …= S

 

Параллельное проецирование

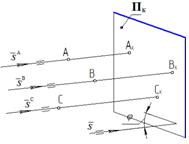S (центрпроецирования) – бесконечно удаленная точка

S º S ^∞

При параллельном проецировании проецирующие прямые параллельны.

S A ∩ S B ∩ S C …= S ^∞

S ^∞ A || S ^∞ B || S ^∞ C || …|| s

s – направление проецирования;  S ^∞ Î s

(s^П_к)=Ð φ

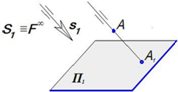
Ð φ =90º Ú (s ^ П_к)Þ косоугольное проецирование

Ð φ =90º Ú (s ^ П_к) Þ ортогональное проецирование (прямоугольное)

 

Свойстваортогональногопроецирования

 

1. Проекция точки есть точка

 

 

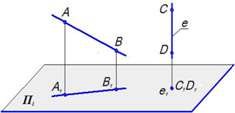2. Если прямая не перпендикулярна плоскости проекций

П₁, то ее проекция – прямая линия.

(AB) ^ П₁ Þ (A ₁ B ₁) - _________________

Если прямая перпендикулярна плоскости проекций П₁,

То ее проекция - точка.

e ^ П₁ Þ e ₁ - ____________________

3. Если прямые параллельны, то их проекции тоже параллельны

a || bÞa₁__b₁

 

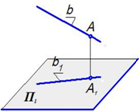
4. Если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой

A Î b Þ A ₁ __ b ₁

 

5. Отношениеотрезков, принадлежащиходнойпрямойравноотношениюихпроекций.

Точка делит отрезок прямой в том же отношении, что проекция этой точки делит проекцию отрезка.

              [ AM ]: [ MB ] = [ ______ ]: [ ______ ]

Одна проекция точки не определяет ее положение в пространстве

Точка A ₁ может быть проекцией любой точки, лежащей на прямой s.

 

Для однозначности чертежа используют проецирование на две и больше плоскости (удваивают аппарат проецирования)

 

Положение точки в пространстве определяется ее проекциями на две плоскости

 

 

Проецирование на две взаимно-перпендикулярные плоскости

Метод Монжа

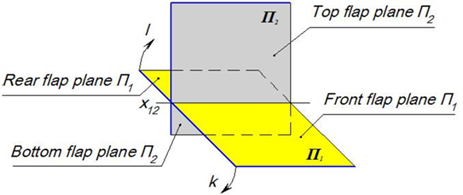
Две плоскости проекций пересекаются под прямым углом

 

П₁ ^ П₂

П₁ ∩ П₂ = x ₁₂

 

П₁ – ___________________________________________

П₂ – __________________________________________

X ₁₂ – __________________________________________

 

 

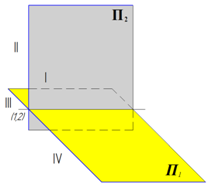
Плоскости П₁ и П₂ делят пространство на четыре четверти

 

 

 

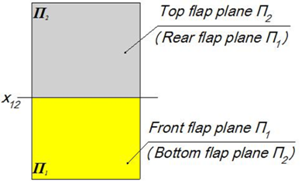
Плоскость П₁ поворачиваетсявокругоси x ₁₂ так, что передняя часть П₁ совпадает ч нижней частьюплоскости П₂

 

Ортогональная проекция точки на плоскостиП₁ и П₂

 

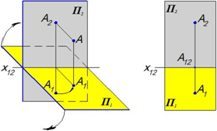
AA ₁ ^ П₁ A ₁ - горизонтальная проекция точки A

AA ₂ ^ П₂ A ₂ - фронтальная проекции точки A

AA ₂ - расстояние от точки Aдо плоскости П₂ AA ₂ = A ₁ A ₁₂ -глубина

AA ₁ –расстояниеотточкиtAдо плоскости П₁ AA ₁ = A ₂ A ₁₂ - высота

А₁А₂ ^ х₁₂

Ортогональные проекции точки на две перпендикулярные плоскости однозначно определяет положение точки в пространстве.

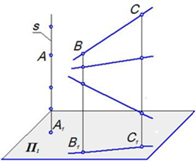
Проекция точек, расположенных в разных четвертях пространства

 

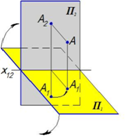Точка A в первой четверти

Горизонтальная проекция лежит под осью x ₁₂, афронтальная проекция лежит выше нее.

 

 

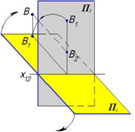
Точка B во второй четверти

Обе проекции выше оси x ₁₂

 

 

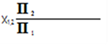
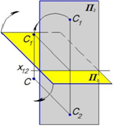
Точка C в третьей четверти

Горизонтальная проекция C₁ выше оси x₁₂, а фронтальная C₂ лежит ниже оси x₁₂

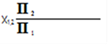
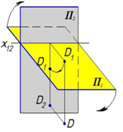
Точка D в четвертой четверти

Обе проекции расположены ниже оси x ₁₂

 

 

 

Прямая линия

Линия рассматривается как след постоянно движущейся в пространстве точки.

Линиимогутбытьпрямыми, ломанымиикривыми

 

l (A, B) Þ A Î l и B Î l

Проекция прямой линии вобщемслучаеявляетсяпрямая линия, которая определяется проекциями двух точек этой прямой