Контрольная работа № 5
Задание 1. Вычислить двойной интеграл по области, ограниченной линиями
| №331. | 
| D: y=x2 , y=0, x=1 |
| №332. | 
| D: y=x2 , y=0, x=2 |
| №333. | 
| D: y=4x2 , y=0, x=1 |
| №334. | 
| D: y=1+x2 , y=1, x=2 |
| №335. | 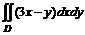
| D: y=x2 , y=1, x=3 |
| №336. | 
| D: y=x2 , y=0, x=1, x=2 |
| №337. | 
| D: y=1+ x3 , y=1, x=4 |
| №338. | 
| D: y=x3 , y=0, x=2 |
| №339. | 
| D: y=x2 , y=2, x=3 |
| №340. | 
| D: y=x3 , y=0, x=3 |
Задание 2. Вычислите с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а>0)
| №341. | (x2 + y2)3=4x2y2 |
| №342. | (x2 + y2)2=25(4x2 + y2) |
| №343. | (x2 + y2)3=9(4x2 + y2) |
| №344. | (x2 + y2)2=4(3x2 + 2y2) |
| №345. | x4 =16(3x2-y2) |
| №346. | x6=9(x4 - y4) |
| №347. | x4 =a(x2 - 3y2) |
| №348. | y6=a2 (y4 - x4) |
| №349. | (x2 + y2)2=a2(2x2 + 3y2) |
| №350. | y6=a2 (x2 + y2) (3y2 + x2) |
Задание 3. Вычислите с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость ХОY.
| №351 | z=0, z=x, y=0, y=3, x= 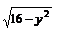
|
| №352. | z=0, z=16–y2, x2+y2 = 16 |
| №353. | z=0, z=25-x-y, x2+y2 = 25 |
| №354. | z=0, z=y2, x2+y2=4 |
| №355. | z=0, y+z=3, x2+y2=9 |
| №356. | z=0, z=4y2, 2x – y =0, x+y = 9 |
| №357. | z=0, z=x2+y2, x2+y2 = 9 |
| №358. | z=0, z=1-y2, x=4y2, x=4y2 +1 |
| №359. | z=0, z=4-x2, y=0, x=4-x |
| №360. | z=0, z=9  , x=0, x+y=9 , x=0, x+y=9
|
Задание 4. Вычислите криволинейный интеграл
| №361. | 
| вдоль дуги L окружности x=5cost, y=5sint, обходя ее против хода часовой стрелки от точки А(5;0) до точки В(0;5). Сделать чертеж. |
| №362. | 
| вдоль ломаной L=ОАВ, где О(0;0), А(-1;1) до точки В(4;5). Сделать чертеж. |
| №363. | 
| вдоль границы L треугольника АВС, обходя ее против хода часовой стрелки, если А(2;0), В(2;2), С(0;2). Сделать чертеж. |
| №364. | 
| вдоль дуги L параболы y= x2 от точки А(-1;1) до точки В(1;1). Сделать чертеж. |
| №365. | 
| вдоль верхней половины L эллипса x=2cost, y=3sint (0<t<  ). Сделать чертеж. ). Сделать чертеж.
|
| №366. | 
| вдоль ломаной L=АВC, где A(1;2), B(1;5), C(3;5). Сделать чертеж. |
| №367. | 
| вдоль дуги L кривой y=e-x от точки А(0;1) до точки В(-1;e). Сделать чертеж. |
| №368. | 
| вдоль отрезка L=АВ прямой от точки А(-1;2) до точки В(-2;4). Сделать чертеж. |
| №369. | 
| вдоль дуги L параболы y=2x2 от точки O(0;0) до точки А(2;8). Сделать чертеж. |
| №370. | 
| вдоль дуги L кривой y=lnx от точки A(1;0) до точки B(e;1). Сделать чертеж. |
Задание 5. Даны векторное поле  и плоскость Ax+By+Cz+D=0 (p), которая совместно с координатными плоскостями образует пирамиду V.
и плоскость Ax+By+Cz+D=0 (p), которая совместно с координатными плоскостями образует пирамиду V.
Пусть  - основание пирамиды, принадлежащее плоскости (р);
- основание пирамиды, принадлежащее плоскости (р);  - контур, ограничивающий
- контур, ограничивающий  ;
;
n –нормаль к  , направленная вне пирамиды V.
, направленная вне пирамиды V.
Требуется вычислить:
1) поток векторного поля F через поверхность  в направлении нормали n;
в направлении нормали n;
2) циркуляцию векторного поля F по замкнутому контуру  и ограниченной им замкнутой поверхности
и ограниченной им замкнутой поверхности  с нормалью n;
с нормалью n;
3) поток векторного поля F через полную поверхность пирамиды V в направлении внешней нормали к ее поверхности, применив теорему Остроградского. Сделать чертеж
| №371. |  x+y+z-2=0 x+y+z-2=0
|
| №372. |  2x-y+2z-2=0 2x-y+2z-2=0
|
| №373. |  x+y+z-4=0 x+y+z-4=0
|
| №374. |  -x+2y+2z-4=0 -x+2y+2z-4=0
|
| №375. | 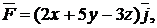 2x-3y+2z-6=0 2x-3y+2z-6=0
|
| №376. | 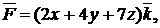 3x+2y+3z-6=0 3x+2y+3z-6=0
|
| №377. |  -x+2y+z-4=0 -x+2y+z-4=0
|
| №378. |  x-y+2z-4=0 x-y+2z-4=0
|
| №379. | 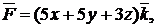 x+y+3z-3=0 x+y+3z-3=0
|
| №380. | 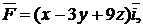 -x+y+2z-4=0 -x+y+2z-4=0
|
Задание 6. Проверить является ли векторное поле  потенциальным и соленоидальным. В случае потенциальности поля
потенциальным и соленоидальным. В случае потенциальности поля  найти его потенциал.
найти его потенциал.
| №381. | 
|
| №382. | 
|
| №383. | 
|
| №384. | 
|
| №385. | 
|
| №386. | 
|
| №387. | 
|
| №388. | 
|
| №389. | 
|
| №390. | 
|
Задание 7. Исследовать сходимость числового ряда 
| №391. |  
|
| №392. | 
|
| №393. | 
|
| №394. | 
|
| №395. | 
|
| №396. | 
|
| №397. | 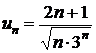
|
| №398. | 
|
| №399. | 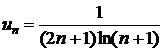
|
| №400. | 
|
Задание 8. Найти интервал сходимости степенного ряда 
| №401. |  
|
| №402. | 
|
| №403. | 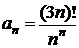
|
| №404. | 
|
| №405. | 
|
| №406. | 
|
| №407. | 
|
| №408. | 
|
| №409. | 
|
| №410. | 
|
Задание 9. Вычислить значение функции с точностью до 0,001, разложив ее в степенной ряд.
| №411. |  при при 
|
| №412. |  при при 
|
| №413. |  при при 
|
| №414. |  при при 
|
| №415. | 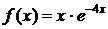 при при 
|
| №416. |  при при 
|
| №417. |  при при 
|
| №418. | 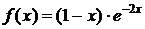 при при 
|
| №419. |  при при 
|
| №420. |  при при 
|
Задание 10. Вычислить определенный интеграл 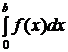 с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и проинтегрировав его почленно.
с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и проинтегрировав его почленно.
| №421. |  при b=1,1. при b=1,1.
|
| №422. |  при b=1,1. при b=1,1.
|
| №423. |  при b=0,6. при b=0,6.
|
| №424. |  при b=0,6. при b=0,6.
|
| №425. |  при b=0,6 при b=0,6
|
| №426. |  при b=0,6 при b=0,6
|
| №427. |  при b=0,6. при b=0,6.
|
| №428. |  при b=1,1. при b=1,1.
|
| №429. |  при b=0.6. при b=0.6.
|
| №430. | 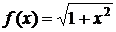 при b=0,6 при b=0,6
|
Задание 11. Найти три первых, отличных от нуля члена разложения в степенной ряд решения y=y(x) дифференциального уравнения  , удовлетворяющего начальному условию
, удовлетворяющего начальному условию  .
.
| №431. | 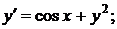 
|
| №432. |  
|
| №433. |  
|
| №434. |  
|
| №435. | 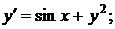 
|
| №436. | 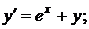 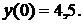
|
| №437. |  
|
| №438. | 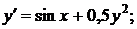 
|
| №439. |  
|
| №440. |  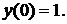
|
Задание 12. Разложите данную функцию  в ряд Фурье в интервале (a;b)..
в ряд Фурье в интервале (a;b)..
| №441. |  , в интервале , в интервале 
|
| №442. |   в интервале в интервале 
|
| №443. |  в интервале в интервале 
|
| №444. |  в интервале в интервале 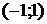
|
| №445. |   в интервале в интервале 
|
| №446. |  в интервале в интервале 
|
| №447. | 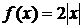 в интервале в интервале 
|
| №448. |  в интервале в интервале 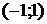
|
| №449. |  в интервале в интервале 
|
| №450. |  в интервале в интервале 
|
Содержание и оформление контрольных работ
5.1 Требования к оформлению контрольной работы: в случае рукописного варианта контрольная работа выполняется в тетради (12л.) на обложке необходимо указать № к.р., свой факультет, специальность, шифр зачетной книжки, номер варианта, ФИО, в случае электронного варианта контрольная работа выполняется в текстовом редакторе Word.
5.2. Требования к структуре контрольной работы:
При выполнении работы необходимо приводить основные теоретические моменты, промежуточные математические доказательства, методики, формулы, расчеты.
В конце работы указывается список использованных источников, ставится число и личная подпись.
6 Темы практических занятий.
1. Двойные интегралы и тройные интегралы. Сведение к повторному. Замена переменных. Некоторые геометрические и физические приложения двойных интегралов.
Литература: [3,гл.13, с.307-324, с. 346-353]
2. Криволинейные интегралы. Вычисление криволинейных интегралов первого и второго рода. Некоторые приложения криволинейных интегралов первого и второго рода. Формула Грина.
Литература: [3,гл.13, с.324-346]
3. Поверхностные интегралы. Формула Остроградского. Формула Стокса. Скалярное и векторное поля. Задача о потоке векторного поля. Дивергенция. Циркуляция. Ротор.
Литература: [ 3,гл.8,с.192-215].
4. Ряды. Свойства сходящихся рядов. Знакочередующиеся ряды. Абсолютная и условная сходимость рядов. Степенные ряды. Интервал сходимости степенного ряда. Разложение функций в степенные ряды. Приближенные вычисления значений функций, определенных интегралов, решений дифференциальных уравнений.
Литература: [3,гл.14,с.379-402]
5.Ряды Фурье в комплексной форме.
Литература: [ 3,гл.14,с.410-416 ]
7. Вопросы для подготовки к экзамену (зачету)
1. Вычисление двойного интеграла через повторный.
2. Замена переменных. Вычисление двойного интеграла в полярной системе координат.
3. Замена переменных в тройном интеграле. Цилиндрическая и сферическая система координат.
4. Вычисление тройного интеграла через повторный.
5. Криволинейные интегралы 1-го рода.
6. Криволинейные интегралы 2-го рода. Формула Грина.
7. Касательная плоскость и нормаль к поверхности. Площадь поверхности. Поверхностные интегралы и их вычисление через двойные интегралы.
8. Векторный анализ и элементы теории поля.
9. Скалярное и векторное поле. Градиент. Поток векторного поля. Дивергенция. Формула Гаусса – Остроградского. Ротор векторного поля. Формула Стокса.
10. Ротор векторного поля. Формула Стокса. Векторные линии и трубки.
11. Бесконечные числовые ряды. Сходимость. Сумма числового ряда.
12. Свойства сходящихся рядов.
13. Признаки сходимости знакопостоянных рядов. Признаки сравнения. Признак Даламбера. Радикальный и интегральный признаки сходимости.
14. Знакочередующиеся ряды. Признак сходимости Лейбница.
15. Функциональные ряды. Поточечная и равномерная сходимость.
16. Непрерывность, интегрируемость и дифференцируемость суммы равномерно сходящихся рядов.
17. Степенные ряды. Основные определения и теоремы.
18. Ряды Тейлора и Маклорена.
19. Вычисление значений функций с помощью степенных рядов.
20. Вычисление определенных интегралов с помощью степенных рядов.
21. Нахождение решений дифференциальных уравнений с помощью степенных рядов.
22. Ортогональные системы функций и обобщенные ряды Фурье.
23. Тригонометрические ряды Фурье. Условия разложимости в ряды Фурье.
24. Разложение функций в ряд по синусам или по косинусам.
25. Тригонометрические ряды Фурье в комплексной форме.
26. Интеграл Фурье. Косинус и синус-преобразование Фурье.
8. Список рекомендуемой литературы
1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Том 2. Учебное пособие для втузов. – М.: Наука, 1985. – 432 с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Часть 2 – М.:Образование, 2002г.
3. Шипачев В.С. Задачник по высшей математике: Учебное пособие для вузов. – 2-е изд., испр. – М.: Высшая школа, 2001г. – 304 с.
4. Шипачев В.С. Высшая математика. Учеб. для вузов. – 5-е изд., стер. – М.: Высшая школа. 2002. – 479 с.
5. Барвин И.И. Высшая математика: Учебное пособие для студентов вузов. –
3-е изд., стереотип. – М.: Издательский центр «Академия», 2002. – 616 с.






