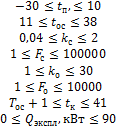Важным показателем холодильной установки, как объекта регулирования, является свойство самовыравнивания (принцип Ле-Шателье): в результате внешних или внутренних возмущений в системе возникают процессы, стремящиеся вернуть параметры работы установки вновь в состояние равновесия. Единственным элементом холодильной установки, препятствующим самовыравниванию, является дроссельный вентиль. Его степень открытия должна подбираться в соответствии с режимом работы установки. Для специалиста-холодильщика представляют интерес, как результат процесса самовыравнивания, так и регулирующие воздействия, которые он может оказывать на холодильную установку с тем, чтобы процесс самовыравнивания завершился при определенном (требуемом) значении регулируемого параметра.
Рассматривается холодильная установка, включающая в себя четыре основных элемента: охлаждающие приборы, компрессор, конденсатор и дросселирующий (регулирующий) вентиль.
Основная цель работы холодильной установки – поддержание заданного температурного режима в охлаждаемом объекте. Обеспечивается это путём отвода с помощью холодильной машины теплопритока, поступающего к охлаждаемому объекту из окружающей среды и в результате внутренних тепловыделений. Если изменение производительности холодильной машины осуществляется методом включения/выключения компрессорного агрегата, то за один цикл работы компрессора, включающий время стоянки и время работы, количество выработанного холода должно соответствовать теплоте, поступающей к охлаждаемому объекту. Достигается такое соответствие изменением величины коэффициента рабочего времени компрессора.
Работу холодильной установки рассмотрим со следующими основными допущениями:
× температура конденсации принята постоянной и не зависящей от режима работы установки;
× переохлаждение холодильного агента после конденсаторов отсутствует;
× перегрев пара 
, всасываемого компрессорами, составляет (5...15) градусов и не изменяется во времени;
× не рассматриваются переходные процессы (например, после включения и выключения компрессора);
× на установке не имеется резерва компрессоров;
× испарительная система не обладает тепловой инерционностью и выключается из работы одновременно с компрессорным агрегатом;
× все охлаждаемые помещения заменены одним условным, равным им по площади, в котором поддерживается постоянная температура.
Для принятых допущений имеет место следующая система уравнений, описывающая работу холодильной установки:
| (3.1) |
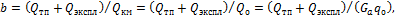
| (3.2) |
| (3.3) |
| (3.4) |
где 
– холодопроизводительность компрессора, Вт; 
– холодопроизводительность приборов охлаждения, Вт; 
– холодопроизводительность регулирующего вентиля, Вт; b – коэффициент рабочего времени компрессора;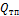 
– теплоприток к охлаждаемому объекту, Вт; Q экспл – теплоприток в камеру от внутренних источников тепла и вентиляции, Вт; F – требуемая площадь проходного сечения регулирующего вентиля, м2; 
– массовый расход холодильного агента через регулирующий вентиль, кг/с; 
– коэффициент расхода холодильного агента через регулирующий вентиль (для аммиака = 0,35...0,4; 
– плотность холодильного агента (жидкого, насыщенного) перед регулирующим вентилем, кг/м3; 
– давления, соответственно, конденсации и кипения холодильного агента, Па; 
– удельная массовая холодопроизводительность холодильного агента, Дж/кг.
Значения давлений конденсации (p к) и кипения (p о) определяются по аппроксимирующей зависимости, полученной по таблицам термодинамических свойств аммиака в состоянии насыщения:
| (3.5) |
где 
– температура конденсации (к) или кипения (о) соответственно, К.
Аналогично получена аппроксимирующая зависимость для плотности насыщенной жидкости перед дроссельным вентилем:
| (3.6) |
Здесь 
− температура конденсации в оС.
Холодопроизводительность компрессора при постоянном перегреве всасываемого пара зависит от температур кипения и конденсации.
Для расчёта холодопроизводительности компрессора данную зависимость можно аппроксимировать уравнением вида:
| (3.7) |
Например, для холодопроизводительности компрессора П-220 (см. рис. П1 приложения) a 0 =72,8; a 1 = 2,264; a 2=-0,613; a 3 = 0,0273.
Удельная массовая холодопроизводительность ХА:
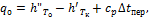
| (3.8) |
где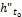 
– удельная энтальпия сухого насыщенного пара хладагента при температуре в испарителе, Дж/кг; 
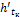– удельная энтальпия насыщенного жидкого хладагента при температуре в конденсаторе, Дж/кг; 
– удельная изобарная теплоёмкость паров хладагента, Дж/(кг К); – перегрев пара хладагента всасываемого компрессором.
Для аммиака значение удельной изобарной теплоёмкости паров определим по формуле для идеально-газового состояния:
| (3.9) |
где 
– газовая постоянная, 
Дж/(кг К); 
– показатель адиабаты аммиака 
).
Холодопроизводительность охлаждающих приборов (батарей):
| (3.10) |
где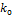 
– коэффициент теплопередачи приборов охлаждения, Вт/(м2 К); 
– площадь поверхности приборов охлаждения, м2.
Наличие в правой части уравнения (3.10) коэффициента рабочего времени компрессора 
указывает на то, что во время стоянки компрессора ни регулирующий вентиль, ни приборы охлаждения не работают, то есть их холодопроизводительность равна нулю (тепловой инерционностью приборов охлаждения в этом случае мы пренебрегаем).
Поток теплоты из окружающей среды в охлаждающее помещение определяют по уравнению теплопередачи:
| (3.11) |
Используя уравнения (3.5) – (3.11), с учётом требуемого равенства холодопроизводительностей компрессора, приборов охлаждения и регулирующего вентиля, при заданной (требуемой) температуре помещения, система уравнений (3.1) – (3.3) может быть решена относительно трех основных неизвестных: t о, F, b, которыми являются равновесная (самоустанавливающаяся) температура кипения, требуемая площадь прохода регулирующего вентиля и коэффициент рабочего времени компрессора. Если задан коэффициент рабочего времени компрессора, например b = 1 (компрессор работает постоянно), помимо t ои F из системы можно определить самоустанавливающуюся температуру помещения t п.
Если графически изобразить в координатах Q – t озависимости (3.6) и (3.9), которые представляют функции холодопроизводительности компрессора и охлаждающих приборов от температуры кипения при (b = 1), то пересечением полученных кривых определяется точка ("рабочая точка"), которая соответствует найденным аналитически параметрам равновесного режима работы установки.
Если расчётное значение коэффициента рабочего времени оказалось больше единицы, то это означает, что одним компрессором требуемую температуру помещения не поддержать.
Считается, что на установке используются компрессоры только одной марки. Холодопроизводительность компрессоров регулируется методом включения/выключения.
Расчетные зависимости характерны в первую очередь для камерных приборов-батарей.
Ограничения на вводимые параметры:
