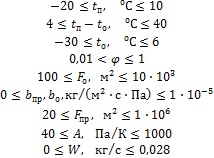Основы математической модели влажностного режима в холодильной камере хранения приводятся в [2].
Равновесный влажностный режим моделируют для камер длительного хранения увлажненных грузов.
Известно, что в процессе холодильной обработки и хранения влажного неупакованного груза (продукта) имеет место его усушка, т.е. испарение влаги с поверхности продукта. Этот процесс сопровождается диффузией влаги из центральных слоев груза к периферийным слоям за счёт разности парциальных давлений водяного пара над поверхностью продукта и в воздухе камеры.
Из воздуха камеры происходит конденсация влаги на поверхности приборов охлаждения, имеющих более низкую температуру t о, чем температура воздуха в помещении t п. Если в камере имеются специальные увлажняющие устройства, создающие постоянный приток влаги к воздуху камеры с целью поддержания определенной влажности, то уравнение влажностного баланса можно записать в следующем виде:
| (2.1) |
где 
– количество влаги, испаряющейся в единицу времени с поверхности продукта, кг/с; 
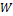– приток влаги от устройств искусственного поддержания влажности (при их отсутствии 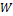= 0), кг/с; 
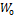– поток влаги, конденсирующейся на приборах охлаждения, кг/с.
Потоками влаги, не учтенными в (2.1), пренебрегаем.
Уравнение для испарения влаги с поверхности продукта на основании закона Дальтона запишем в следующем виде:
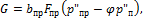
| (2.2) |
где 
– коэффициент испарения влаги с поверхности продукта, кг/(м2∙с∙Па); 
– равновесная относительная влажность;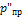 
– давление насыщенного водяного пара над поверхностью продукта, Па; 
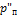– давление насыщенного водяного пара в воздухе помещения, Па.
Уравнение для конденсации влаги на приборах охлаждения:
| (2.3) |
где 
– коэффициент конденсации влаги на поверхности приборов охлаждения, кг/(м2∙с∙Па); F о – суммарная площадь поверхностей воздухоохладителей, м2; 
– давление насыщенного водяного пара над поверхностью охлаждающих приборов, Па.
Уравнение тепло-влажностного баланса продукта с учетом допущения, что вся теплота, подводимая к продукту (вследствие испарения влаги с его поверхности температура продукта ниже, чем температура воздуха, в котором он хранится), расходуется на испарение влаги с его поверхности, имеет вид:
| (2.4) |
где 
– коэффициент теплоотдачи продукта, Вт/(м2 К); 
– удельная теплота парообразования, Дж/кг.
Систему уравнений (2.1) – (2.4) необходимо дополнить аппроксимирующей зависимостью, устанавливающей связь между давлением насыщения водяного пара и температурой (эта зависимость получена при выполнении работы 1):
| (2.5) |
Система уравнений (2.1) – (2.5) для решаемой задачи с учетом принятых допущений является замкнутой.
При определении равновесной влажности и отсутствии искусственного притока влаги (W =0) в системе семь неизвестных: , 
, , 
, , , .
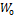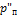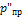Если задается требуемая влажность ,то эта величина исключается из числа неизвестных, тогда седьмой величиной становится требуемая (неизвестная) величина притока влаги W, необходимого для поддержания заданной влажности.
Во всех случаях справедлива одна и та же система уравнений.
Для удобства работы вводится вспомогательное понятие психрометрического коэффициента (психрометрического фактора) А, вычисляемого по формуле:
| (2.6) |
Тогда уравнение (2.4) с учетом выражения для 
примет следующий вид:
| (2.7) |
Ограничения на вводимые параметры:
