Толщина тепловой изоляции непосредственно влияет на капитальные затраты при строительстве холодильной установки и на эксплуатационные затраты, связанные с выработкой холода для компенсации теплопритоков, поступающих через изоляцию на протяжении всего периода эксплуатации. Так как полные приведенные годовые затраты на производство холода представляют собой аддитивную целевую функцию (ФЦ), то влияние теплоизоляции на ФЦ учитывается через слагаемые, которые зависят только от характеристик теплоизоляции (l из, Ц из, В из).
Суммарные затраты, руб/год
 ,
| (4.1) |
где 
– затраты, связанные собственно с изоляцией; 
– затраты на производство холода.
Величина может быть определена через капитальные затраты на изоляцию
 ,
| (4.2) |
где 
– коэффициент, учитывающий затраты на сооружение изоляционных конструкций (стоимость монтажных работ и транспортировки составляют 12% и 4% от стоимости материала изоляции, соответственно), =1,16; 
– суммарная стоимость материала изоляции, руб; 
– доля амортизационных отчислений от капитальных затрат (
0,101 для холодильного оборудования рыбной промышленности), 1/год; 
– нормативный коэффициент окупаемости капитальных вложений (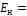
0,0625), 1/год.
Суммарная стоимость материала изоляции определяется, исходя из требуемого количества и цены
 ,
| (4.3) |
где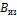 
– толщина изоляции, м; 
– площадь изоляции, м2; 
– цена изоляции, руб/м3.
Величину годовых затрат на производство холода можно оценить по следующей зависимости
| (4.4) |
где 
– теплоприток через ограждения, Вт; 
– цена холода, руб/Дж; 
– время работы холодильной установки в течение года, час; 
– зависимость холодильного коэффициента холодильной машины принятого типа от температур кипения 
и конденсации 
.
Холодильный коэффициент равен:
| (4.5) |
где 
– зависимость холодопроизводительности холодильной машины от температур кипения и конденсации ; 
– зависимость эффективной мощности компрессора холодильной машины от температур кипения и конденсации .
Теплоприток через ограждения
 ,
| (4.6) |
где 
– коэффициент теплопередачи изоляции, Вт/(м2 К); 
– среднегодовая температура окружающей среды, °С; 
– температура воздуха в охлаждаемом помещении, °С.
Коэффициент теплопередачи теплоизоляции без учёта термических сопротивлений несущих и отделочных конструкций холодильника
| (4.7) |
где 
– коэффициент теплоотдачи с наружной стороны ограждения, Вт/(м2 К);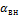 
– коэффициент теплоотдачи с внутренней стороны ограждения, Вт/(м2 К); 
– коэффициент теплопроводности материала изоляции, Вт/(м К).
Оптимальную толщину изоляции, т.е. ту, при которой приведенные затраты принимают минимальное значение, можно определить двумя способами: 1) аналитическим, на основе метода классического анализа функций; 2) численным.
При определении (B из)оптметодом классического анализа функций необходимо продифференцировать выражение для суммарных приведенных затрат по толщине изоляции и приравнять к нулю 
. Полученное уравнение необходимо решить относительно 
| (4.8) |
При определении (B из)оптчисленным методом необходимо записать целевую функцию в виде суммарных приведённых затрат
| (4.9) |
задать ограничения на варьируемый параметр (предполагаемые разумные пределы изменения 
) и воспользоваться программой поиска минимума этой функции.
