Отыскание интервалов выпуклости и точек перегиба

Достаточное условие выпуклости функции на интервале.

Если вторая производная f"(х) существует на интервале (а, b) и не меняет знак на этом интервале, то:

1) при f"(х) > 0 (знак +) функция f(х) выпукла вниз на интервале (а;b);

2) при f"(х) < 0 (знак -) функция f(х) выпукла вверх на интервале (а;b).

Таким образом, для нахождения интервалов выпуклости вверх и выпуклости вниз функции нужно найти вторую произ­водную и решить неравенства
  f "(х) < 0 и f "(х) > 0.

Точка М₀ (х₀; f (х₀)) графика функции у = f (х) называется точкой перегиба этого графика, если существует такая окрестность точки х₀, в пределах которой график функции у = f (х) слева и справа от т. М₀ имеет разные направления вы­пуклости.

На рис. 5 изображен график функции, имеющей перегиб в точке М₀(х₀; f (х₀)).

Рис. 5.  График функции, имеющей перегиб

 

Необходимый признак существования точки перегиба.

  Если функция в точке х₀ имеет перегиб, то вторая производная в этой точке либо не существует, либо равна нулю.

Точки, в которых вторая производная обращается в нуль или не существует, называют критическими точками II-го рода. В этих точках перегиб может быть, а может и не быть. Этот вопрос ре­шается с помощью следующего признака.

Достаточный признак существования точки перегиба.

Пусть функция определена и непрерывна в некоторой окрестности точки х₀, включая саму точку. Пусть, далее, вторая производ­ная в этой точке равна нулю или не существует. Тогда, если f"(х) < 0 при х <х₀ и f"(х) > 0 при х > х₀ или f"(х) > 0 при х < х₀ и f"(х) < 0 при х > х₀, то М₀(х₀, (f(х₀)) является точкой перегиба кривой  у = f(х).

 

II. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ

Понятие предела функции

Число А называется пределом функции в точке х₀ (или при х х₀), если для любого положительного числа  найдется такое положительное число , что для всех х х_{0 ,} удовлетворяющих неравенству 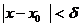, выполняется неравенство .

Обозначают

Бесконечно малые и бесконечно большие функции

Функция  называется бесконечно малой при , если .

Функция  называется бесконечно большой при , если  или .

Теоремы о пределах

1.

2.

3.

4.

5.

Первый замечательный предел 

Второй замечательный предел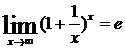            

Правило Лопиталя.

  Пусть функции    и  непрерывны и дифференцируемы в окрестности точки x₀ и обращаются в нуль в этой точке: 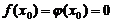. Пусть  в окрестности точки x₀. Если существует предел , то .

 

Односторонние пределы

Бывают случаи, когда способ приближения аргумента х к х₀ существенно влияет на значение предела функции. Поэтому вводят понятия односторонних пределов.

Число А₁ называется пределом функции y = f (x) слева в точке х₀, если для любого числа  существует число  такое, что при х  выполняется неравенство . Предел слева записывают так:  или коротко:  (обозначение Дирихле).

Аналогично определяется предел функции справа. Число А₂ называется пределом функции y = f (x) справа в точке х₀, если для любого числа  существует число  такое, что при х  выполняется неравенство 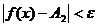. Предел справа записывают так: . Коротко предел справа обозначают f (x_o +0)= A ₂.

Пределы функции слева и справа называются односторонними пределами.

Непрерывность функции

Функция  называется непрерывной в точке , если предел функции при  равен значению функции при :

.

А также говорят, функция  называется непрерывной в точке , если она в этой точке определена, и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т. е.

.

Существует теорема о непрерывности функции в точке. Функция y= f(x) непрерывна в точке x₀, тогда и только тогда, когда функция имеет конечные пределы в точке x₀ и предел функции в точке x₀ равен значению функции в этой точке.

Все элементарные функции непрерывны в области своего определения.

Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.

Для элементарных функций справедливы следующие положения:

1. область непрерывности элементарной функции совпадает с её областью определения, т.е. элементарная функция непрерывна во всей области определения

2. элементарная функция может иметь разрыв только в отдельных точках какого-либо промежутка, но не во всех его точках

3. элементарная функция может иметь разрыв только в той точке, в которой она не определена.

Функция называется непрерывной в промежутке (замкнутом или открытом), если она непрерывна во всех точках этого промежутка.

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.

Точка разрыва х₀ называется точкой разрыва первого рода функции , если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е  и .

При этом:

если А₁=А₂, то точка х₀ называется точкой устранимого разрыва (рис.6)

если , то точка х₀ называется точкой конечного разрыва (рис.7).

Величину  называют скачком функции

 

Рис. 6. График функции с устранимым разрывом

Рис. 7. График функции с конечным разрывом

 

Точка х₀ называется точкой разрыва 2-го рода, если по крайней мере один из односторонних пределов не существует или равен ∞ (рис.8).

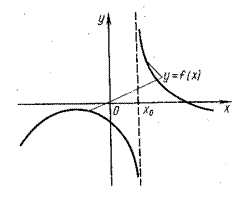
Рис. 8. График функции с точкой разрыва 2-го рода