I. Функция. Свойства функции

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МОСКОВСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ВЕТЕРИНАРНОЙ МЕДИЦИНЫ И БИОТЕХНОЛОГИИ ИМ. К.И. СКРЯБИНА»

_______________________________________________________________

 

 

Джугели Т.П, Кишкинова О.А, Кутликова И.В, Федькина Т.В.

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

ФУНКЦИЯ ОДНОЙ ПЕРМЕННОЙ.

ПРЕДЕЛ ФУНКЦИИ.

ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА.

 

 

Москва 2011

УДК

 

Джугели, Т.П. Функция одной переменной. Предел функции. Исследование функции и построение графика: учеб.-метод. указ. / Т.П. Джугели,
О.А. Кишкинова, И.В. Кутликова, Т.В. Федькина. – М.: ФГБОУ ВПО
МГАВМиБ им. К.И. Скрябина, 2011. – 38 с.

 

В методических указаниях приведены необходимые теоретические сведения и формулы, даны решения типовых задач, приведены задания для расчетно-графической работы по разделу математики «Функция одной переменной. Предел функции. Исследование функции и построение графика».

 

Рекомендованы для студентов очной формы обучения по специальностям 111900.62 - «Ветсанэкспертиза», 111100 –«Зоотехния», 100800 – «Товароведение», 260200 – «Продукты питания животного происхождения», 260100 – «Продукты питания из растительного сырья», 020400 - «Биология»,
240700 – «Биотехнологи».

 

Рецензенты:

профессор ФГБОУ ВПО МГАВМиБ им. К.И. Скрябина А.С. Белановский

 

Утверждены на заседании учебно-методической комиссии ветеринарно-биологического факультета ФГБОУ ВПО МГАВМиБ им. К.И. Скрябина
(протокол № 1 от 13 сентября 2011 г.)

 

ВВЕДЕНИЕ

Целью настоящих методических указаний по теме «Функция одной переменной. Предел функции. Исследование функции и построение графика» является познакомить студентов с теоретическим материалом, который необходим для подготовки высококвалифицированных специалистов в области сельского хозяйства и научной деятельности студентов в биологии и биотехнологии.

В методических указаниях рассмотрены понятие функции, основные её свойства, понятие предела функции, непрерывности функции и приложения дифференциального исчисления к исследованию функции и построению её графика. Разобраны примеры нахождения предела функции, исследование функции и построение графиков, а также приведены варианты индивидуальной контрольной работы студентов и тестовые задания по данному разделу дисциплины.

Одной из основных форм работы студента является самостоятельная работа над учебным материалом. Она состоит из непрерывной работы по изучению теоретического материала, по выполнению текущих заданий и контрольных работ. Результативность самостоятельной работы обеспечивается эффективной системой контроля, которая включает в себя опросы студентов по содержанию лекций, тестирование по отдельным разделам дисциплины, контрольные работы.

При выполнении и оформлении домашней контрольной работы по теме «Исследование функции одной переменной» студент должен придерживаться следующих правил:

а) в заголовке контрольной работы должны быть ясно выписаны фамилия студента, его инициалы, номер задания;

б) контрольную работу следует выполнять в отдельной тетради, обязательно чернилами (не красными), с оставлением полей для замечаний преподавателя;

в) решения контрольных задач следует располагать в порядке номеров, указанных в заданиях; перед решением каждой задачи надо выписывать полностью ее условие;

г) графики функции должны быть выполнены на миллиметровой бумаге с указанием точек экстремума функции, точек перегиба, асимптот функции, единичных отрезков и осей координат.

Контрольная работа, выполненная небрежно, без промежуточных вычислений, с пропуском задач и без соблюдения изложенных выше правил, возвращается обратно для переработки. Контрольная работа, выполненная не по своему варианту, не проверяется. Номер варианта соответствует номеру студента в списке группы.

 

I. ФУНКЦИЯ. СВОЙСТВА ФУНКЦИИ

Понятие числовой функции

Пусть задано числовое множество Х. Правило, сопоставляющее каждому числу х из множества Х единственное действительное число у, называют

числовой функцией, заданной на множестве Х.

х - независимая переменная (аргумент);

 у - зависимая переменная (функция).

Символическая запись функции имеет вид   у = f (х)

Множество Х называется областью определения функции у и обозначается   D (у). Е(у) -   область (множество) значений функции у – множество всех значений переменной у, которые она принимает при всех допустимых значениях х.

1.2. Четность функции

Функция у = f (х) называется четной, если для любого значения х, взятого из области определения функ­ции, значение -х также принадлежит области определения и вы­полняется равенство f (х) = f (-х).

Согласно определению, четная функция определена на мно­жестве, симметричном относительно начала координат. График четной функции симметричен относительно оси ординат (рис. 1).

Рис. 1. График четной функции

Примеры четных функций:

Функция у = f (х) называется нечетной, ес­ли для любого значения х, взятого из области определения функции, значение -х также принадлежит области опреде­ления и выполняется равенство f (x)= - f (x).

График нечетной функции симметричен относительно начала координат (рис. 2).

Примеры нечетных функций:

 

Рис. 2. График нечетной функции

 

При построении графиков четных и нечетных функций доста­точно построить только правую ветвь графика — для положи­тельных значений аргумента. Левая ветвь достраивается симметрично относительно оси о y для четной функции и кососимметрично (т. е. симметрично относительно начала координат) для нечетной.

Конечно, большинство функций не являются ни четными, ни нечетными. Таковы, например, функции: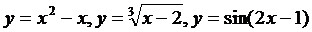

Периодичность

Функция у= f (х) называется периодической с периодом , если при всех значениях х из области её определения выполняются равенства .

Если Т – период функции, то при любом \  число  также является периодом функции.

Наименьший положительный период функции называется её основным периодом.

Сумма, разность, произведение и частное двух функций, имеющих период Т, обладает тем же периодом.

Сумма n периодических функций с периодами  имеет период . Если функция у = f (х) имеет период Т, то функция 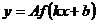 имеет период .

Нули функции

Нулем функции называется такое действительное значение х, при котором значение функции равно нулю.

Для того чтобы найти нули функции, следует решить уравне­ние f (х)=0. Действительные корни этого уравнения являются нулями функции у= f (х),и обратно. Нули функции представляют собой абсциссы точек, в которых график этой функции либо пе­ресекает ось абсцисс, либо касается ее. Например, функция у = х³- 3 x имеет нули в точках х = 0, , , 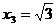а функция  имеет нуль в точке х = 2.

Функция может и не иметь нулей. Такова, например, функция

Монотонность функции.

Переменную величину называют монотонной, если она изменяется только в одном направлении, т.е. либо только возрастает, либо только убывает. Очевидно, что движение точки х в сторону положительного направления оси абсцисс является мо­нотонно возрастающим, а в противоположную сторону - монотонно убывающим.

Функция у = f (х) называется монотонно возрастающей на интервале (а, b), если для любых х₁, и х₂, при­надлежащих этому интервалу, из неравенства х₂ > х₁, следует неравенство f (х ₂ ) > f (x ₁ ) (рис. 3а).

Функция у = f(х) называется монотонно убывающей на интервале (а, b), если для любых х₁ и х₂, принад­лежащих этому интервалу, из неравенства   х₂ > х₁, следует неравенство f (x₂ ) < f (x ₁) (рис. 3б).

Рис. 3. Графики монотонно возрастающей и монотонно убывающей функций.

 

Естественно, что интервал (а, b)предполагается взятым из области определения функции.