Часто реальные установки содержат различное число движущихся компонентов, в том числе взаимосвязанных. Например, крановая тележка, крюк с грузом, мостовой кран управляются отдельно по каждому механизму, однако движение одного (например, крана) вызывает движение и других, связанных с ним механизмов.
Пусть установка состоит из 2-х механизмов, причем механизм 2 связан с механизмом 1 (рисунок 2.3).
| Форма |
| Form.ClientWidth |
| Left1 |
| Top1 |
| Shape2 |
| Left2 |
| Top2 |
| LeftMin |
| LeftMax |
| TopMin |
| TopMax |
| Width1 |
| Width2 |
| Height1 |
| Height2 |
| x 1 |
| y 1 |
| Мех.2 |
| y 2 |
| d 1 |
| h 1 |
| h 2 |
| d 2 |
| L |
| x |
| y |
| X max |
Рисунок 2.3
Механизм 1 может перемещаться как в горизонтальном, так и в вертикальном направлениях, а механизм 2 только вдоль механизма 1. Обозначим реальные координаты механизма 1 через x 1 y 1, а положение механизма 2 относительно механизма 1 через y 2 (рисунок 2.3). Максимальное перемещение механизма 1 по координате x равно L, а по координате y равно H. Геометрические размеры механизма 1 – h 1, d 1, а механизма 2 – h 2, d 2.
Сначала необходимо определиться с масштабом пересчета координат. Дело в том, что для сохранения пропорций необходимо иметь один и тот же масштаб по вертикали и горизонтали. Однако форма может иметь разные пропорции и если перемещение объектов по одной оси в форму помещается, то по другой может выйти за пределы формы.
Определим необходимый масштаб.
1. Длина отрезка по осям x и y, в котором перемещаются оба механизма с учетом их геометрических размеров (рисунок 2.3):
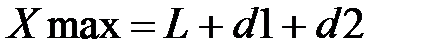 ;
;
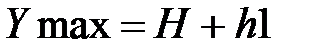 .
.
2. Примем ограничения перемещения объектов по форме в горизонтальном направлении 10% и 90% ширины соответственно. Ограничения по вертикали составляют 10% сверху и 70% высоты снизу (снизу будут располагаться органы управления механизмами). Поэтому масштабы пересчета по оси x и y равны:
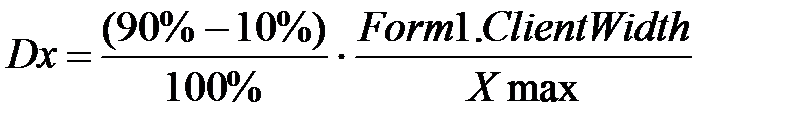 ;
;
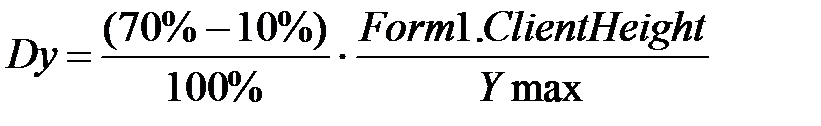 .
.
3. Конечный масштаб принимается по минимальному значению между Dx и Dy:
 . (2.2)
. (2.2)
4. Размеры объектов на форме должны быть пропорциональны геометрическим размерам механизмов с учетом выбранного масштаба:
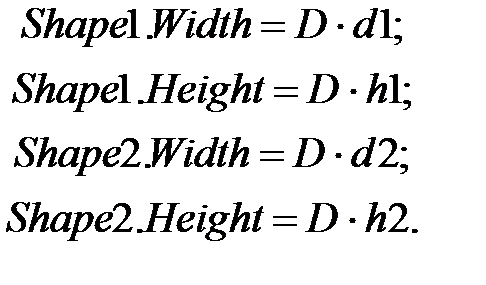
5. Положение объекта Shape1 (механизм 1) на форме рассчитывается по формулам:
 (2.3)
(2.3)
6. Положение объекта Shape2 (механизм 2) на форме рассчитывается с учетом ширины механизма 1 и его положения:
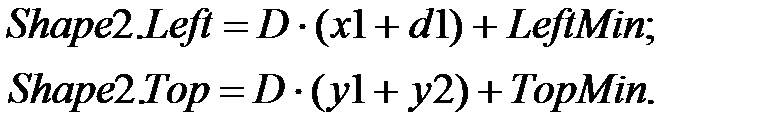 (2.4)
(2.4)
Дифференциальные уравнения
Дифференциальные уравнения движения
Из курса физики известно, что движение объектов может быть упрощенно описано дифференциальными уравнениями первого порядка:

где x (t) – путь, пройденный объектом;
v (t) - скорость объекта;
a (t) – ускорение объекта;
t – время.






