Содержание учебного материала. Вычисление пределов с помощью замечательных пределов, раскрытие неопределенностей. Вычисление односторонних пределов, классификация точек разрыва.
Цель работы: закрепить знания, умения и навыки по применению замечательных пределов к решению пределов другого вида, по раскрытию неопределенностей вида 0/0 и ∞/∞, по решению односторонних пределов; закрепить умение определять вид точек разрыва.
Литература:
[ ОЛ-1 ] Глава 2, § 5.1 – 5.5, стр. 97 - 115,
[ ОЛ-2 ] Глава 5, § 5.1 – 5.2, стр. 53 - 58
[ ОЛ-3 ] Глава 6, § 1 - 6, стр. 76 – 86
Вопросы для повторения:
1. Определение предела.
2. Свойства предела.
3. Определение бесконечно малой и бесконечно большой величины.
4. Замечательные пределы.
5. Односторонние пределы.
6. Определение функции, непрерывной в точке и на промежутке.
7. Определение точки разрыва функции.
8. Классификация точек разрыва функции.
Указания к выполнению работы: составьте предел или функцию, используя предложенные в варианте параметры.
| Вариант | Параметры | Вариант | Параметры | ||||
| a | b | c | a | b | c | ||
| 1 | 1 | -15 | 1 | 6 | 4 | -12 | 7 |
| 2 | -1 | 15 | 2 | 7 | -4 | 12 | 8 |
| 3 | 2 | -14 | 3 | 8 | 5 | -11 | 9 |
| 4 | -2 | 14 | 4 | 9 | -5 | 11 | 10 |
| 5 | 3 | -13 | 5 | 10 | 6 | -10 | 11 |
Задания:
1. Вычислить предел.
| а) | 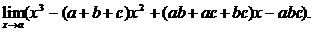
| з) | 
|
| б) | 
| и) | 
|
| в) | 
| к) | 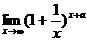
|
| г) | 
| л) | 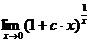
|
| д) | 
| м) | 
|
| е) | 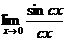
| н) |  . .
|
| ж) | 
| о) | 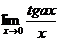
|
2. Исследовать функцию на непрерывность в точке или на промежутке, определить вид точек разрыва функции при их наличии. В задании г) постройте график функции
а)  ,
,  ; б)
; б)  ;
;
в)  ; г)
; г) 
Практическая работа №5
По теме 3.2 Дифференциальное исчисление функции
Содержание учебного материала. Вычисление производных сложных функций. Производные высших порядков. Правила Лопиталя. Дифференциалы высших порядков. Полный дифференциал.
Цель работы: закрепить знания, умения и навыки по вычислению производных сложных функций и производных высшего порядка, по применению правила Лопиталя к раскрытию неопределенностей вида 0/0 и ∞/∞.
Литература:
[ ОЛ-1 ] Глава 6, § 6.1 – 6.3, стр. 116 - 129,
[ ОЛ-2 ] Глава 6, § 6.1 – 6.2, стр. 59 - 66
[ ОЛ-3 ] Глава 7, § 1 - 8, стр. 92 – 104
Вопросы для повторения:
1. Определение производной.
2. Формулы дифференцирования.
3. Правила дифференцирования.
4. Геометрический и физический смысл производной.
5. Формулы дифференцирования сложной функции.
6. Производная второго порядка и её физический смысл.
7. Производная высшего порядка (n-ого порядка).
8. Правило Лопиталя по раскрытию неопределенностей вида 0/0 и ∞/∞.
Указания к выполнению работы: составьте функцию или предел, используя предложенные в варианте параметры.
| Вариант | Параметры | Вариант | Параметры | ||||
| a | b | n | a | b | n | ||
| 1 | 2 | 3 | 2 | 6 | 2 | 4 | 2 |
| 2 | 3 | 4 | 3 | 7 | 3 | 5 | 3 |
| 3 | 4 | 5 | 2 | 8 | 4 | 6 | 3 |
| 4 | 5 | 6 | 2 | 9 | 5 | 7 | 2 |
| 5 | 6 | 7 | 3 | 10 | 6 | 8 | 2 |
Задания:
1. Вычислить производные сложных функций.
| a) | 
| д) | 
|
| б) | 
| е) | 
|
| в) | 
| ж) | 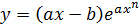
|
| г) | 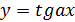
| з) | 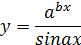
|
2. Найти производные третьего порядка для функций
а)  б)
б) 
3. Вычислить предел, используя правило Лопиталя.
а)  б)
б) 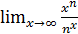
Практическая работа №6






