Методические рекомендации
По выполнению практических работ
по дисциплине
ЕН.01 Элементы высшей математики
по специальности СПО
Программирование в компьютерных системах
г. Благовещенск, 2018г.
Разработчик:
ГБПОУ БМПК преподаватель Алпатикова Н.Г.
Рассмотрено на заседании ПЦК информационно-математических дисциплин, специальности 230115 и профессии 180103.01
Председатель ПЦК Шабаева Е.В.
Оглавление
| Тема | Стр. |
| Пояснительная записка …………………………………………………….. | 4 |
| Литература к практическим работам…………………………………….. | 5 |
| Практическое занятие №1…………………………………………………. по теме 1.1 Матрицы и определители | 6 |
| Практическое занятие №2……………………………………………….… по теме 1.2 Системы линейных уравнений | 7 |
| Практическое занятие №3…………………………………………………. по теме 2.1Прямая на плоскости. Кривые второго порядка Практическое занятие №4…………………………………………………. по теме 3.1 Теория пределов. Непрерывность функции | 9 11 |
| Практическое занятие №5 ………………………………………………… по теме 3.2 Дифференциальное исчисление функции | 12 |
| Практическое занятие №6 ………………………………………………… по теме 3.2 Дифференциальное исчисление функции | 13 |
| Практическое занятие №7 …………………………………….………….. по теме 3.2 Дифференциальное исчисление функции | 14 |
| Практическое занятие №8 ………………………………………………… по теме 3.3 Интегральное исчисление функции | 15 |
| Практическое занятие №9 ……………………………………….……….. по теме 3.3 Интегральное исчисление функции | 17 |
| Практическое занятие №10 ……………………………………….……….. по теме 3.3 Интегральное исчисление функции Практическое занятие №11 ……………………………………………….. по теме 3.4 Дифференциальное исчисление функции нескольких действительных переменных Практическое занятие №12 ……………………………………………….. по теме 3.4 Дифференциальное исчисление функции нескольких действительных переменных Практическое занятие №13 ……………………………………………….. по теме 3.5 Интегральное исчисление функции нескольких действительных переменных Практическое занятие №14………………………………………………. по теме 3.5 Интегральное исчисление функции нескольких действительных переменных Практическое занятие №15 ……………………………………………….. по теме 3.6 Обыкновенные дифференциальные уравнения Практическое занятие №16 ……………………………………………….. по теме 3.6 Обыкновенные дифференциальные уравнения | 19 20 21 22 23 23 24 |
| Практическое занятие №17 ………………………………………………. по теме 4.1 Понятие комплексного числа. Действия над комплексными числами Практическое занятие №18 ………………………………………………. по теме 4.1 Понятие комплексного числа. Действия над комплексными числами | 25 26 |
Пояснительная записка
Общие цели и задачи практических работ.
В рамках традиционного подхода:
1) показать значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы;
2) способствовать развитию умения решать прикладные задачи в области профессиональной деятельности средствами математики;
3) актуализировать знания студентов из курса математики по теме занятия;
4) создать условия для развития творческой активности, самостоятельности и критичности мышления, умения работать в коллективе.
В рамках компетентностного подхода:
1) способствовать выработке у студента умений организовать собственную деятельность, определять методы и способы выполнения задач обучения, оценивать их эффективность и качество;
2) способствовать выработке у студента умений решать проблемы, принимать решения в нестандартных ситуациях;
3) способствовать выработке у студента умений осуществлять поиск, анализ и оценку информации;
4) содействовать использованию студентом информационно-коммуникационные технологии для совершенствования учебной деятельности
5) способствовать выработке у студента умения самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации;
6) содействовать развитию у студента общих и профессиональных компетенций (аналитико-синтетической, прогностической, проектировочной).
К моменту проведения практического занятия по определенной теме в соответствии с рабочей программой студентами, как правило, уже изучен теоретический материал и разобраны основные задачи по данной теме.
Продолжительность времени на выполнение практической работы по каждой теме определяется рабочей программой по дисциплине «Математика».
К каждому практическому занятию приводится перечень литературы, в которой содержатся теоретические сведения по теме занятия и образцы решения задач, с указанием страниц. Возможно использование литературы, как в бумажном, так и в электронном варианте.
Варианты заданий определяются в соответствии со списком студентов по дисциплине «Математика» в учебном журнале группы, при этом в случае двузначного номера в списке нужному варианту соответствует вторая цифра номера. Практические работы оформляются в отдельной тетради. По усмотрению преподавателя по любой практической работе может быть устроена защита.
Литература к практическим работам
| Вид ссылки на указанный источник в тексте практического занятия | |
| Основная литература: 1. Григорьев В.П. Элементы высшей математики: учебник для студ. учреждений сред. проф. образования. – М., «Академия», 2010. 2. Григорьев В.П. Сборник задач по высшей математике: учеб. пособие для студ. учреждений сред. проф. образования. – М., «Академия», 2010. 3. Богомолов Н.В. Практические занятия по математике: учеб. пособие для средних проф. учеб, заведений - М.: Высш. шк., 2009. 4. Спирина М.С., Спирин П.А. Дискретная математика: учебник для студ. учреждений сред. проф. образования. – М., «Академия», 2009. | [ ОЛ-1 ] [ ОЛ-2 ] [ ОЛ-3 ] [ ОЛ-4 ] |
| Дополнительная литература: 1. Богомолов Н.В. Самойленко П.И. Математика - М.: «Дрофа», 2010. 2. Богомолов Н.В. Сборник задач по математике: Учеб. пособие для средних проф. учеб. заведений - М.: «Дрофа», 2009. 3. Дадаян А.А. Математика: Учебник. - М.: Форум Инфра-М, 2011. 4. Гмурман В.Е. «Руководство к решению задач по теории вероятностей и математической статистике». – М: Высшая школа, 2010 5. Бычков А.Г. Сборник задач по теории вероятностей, математической статистике и методам оптимизации: учебное пособие. – М., ФОРУМ, 2008. | [ ДЛ-1 ] [ ДЛ-2 ] [ ДЛ-3 ] [ ДЛ-4 ] [ ДЛ-5 ] |
Интернет-ресурсы
1. www.exponenta.ru – сборник сайтов по математике
2. www.fxyz.ru – интерактивный справочник по алгебре, геометрии, физике
3. www.mccme.ru – московский центр непрерывного математического образования, свободно распространяемые математические книги
4. http://www.yotx.ru/; http://www.aiportal.ru – построение графиков функций онлайн.
Практическая работа №1
по теме 1.1 Матрицы и определители
Содержание учебного материала. Операции над матрицами. Вычисление определителей. Нахождение обратной матрицы. Вычисление ранга матрицы.
Цель работы: закрепить знания, умения и навыки по выполнению операций над матрицами, вычислению определителей, по нахождению матрицы, обратной к данной, вычислению ранга матрицы.
Литература:
[ ОЛ-1 ] Глава 2, § 2.1 – 2.3, стр. 12 - 36,
[ ОЛ-2 ] Глава 2, § 2.1 - 2.2, стр. 7 - 12
Вопросы для повторения:
1. Определение матрицы.
2. Виды матриц: квадратная, треугольная, ступенчатая, единичная, нулевая, вектор-матрица (матрица-строка, матрица-столбец), транспонированная матрица.
3. Операции над матрицами, их свойства.
4. Минор элемента. Алгебраическое дополнение элемента.
5. Союзная матрица. Обратная матрица.
6. Определитель. Определитель второго и третьего порядка.
Указания к выполнению работы: вычисление определителя проводить, используя любой удобный способ – применяя правило треугольника или разложение по строке (столбцу).
Задания:
1. Найти матрицу D = (4А)т +В2 -5С+4Е, где Е – единичная матрица.
2. Вычислить определитель матриц А и К.
3. Найти матрицу, обратную матрице В.
| Вариант | Матрица А | Матрица В | Матрица С | Матрица К |
| 1 | 
| 
| 
| 
|
| 2 | 
| 
| 
| 
|
| 3 | 
| 
| 
| 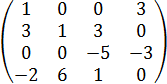
|
| 4 | 
| 
| 
| 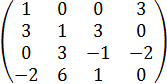
|
| 5 | 
| 
| 
| 
|
| 6 | 
| 
| 
| 
|
| 7 | 
| 
| 
| 
|
| 8 | 
| 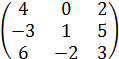
| 
| 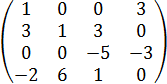
|
| 9 | 
| 
| 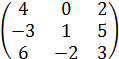
| 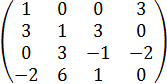
|
| 10 | 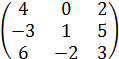
| 
| 
| 
|
Практическая работа №2




