Примеры
10.1. Вычислить поверхностный интеграл первого рода 
, где поверхность S определяется соотношениями 
.
10.2. Вычислить поверхностный интеграл первого рода 
, где поверхность S определяется соотношениями 
.
10.3. Вычислить поверхностный интеграл первого рода 
, где поверхность S есть часть параболоиды 
, отсекаемая плоскостью z = 1.
10.4. Вычислить поверхностный интеграл первого рода 
, где поверхность S определяется соотношениями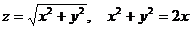 
.
10.5. Вычислить поверхностный интеграл первого рода 
, где S есть часть конической поверхности, заключенная между плоскостями z = 0 и z =1.
10.6. Вычислить поверхностный интеграл второго рода 
, где поверхность S есть внешняя сторона сферы 
.
10.7. Вычислить поверхностный интеграл второго рода 
, где поверхность S есть внешняя сторона конуса 
.
10.8. Вычислить поверхностный интеграл второго рода 
, где поверхность S есть нижняя сторона части конической поверхности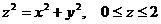 
.
10.9. Вычислить поверхностный интеграл второго рода 
, где поверхность S есть внешняя сторона полусферы 
.
10.10. Вычислить поверхностный интеграл второго рода , где поверхность S есть полусфера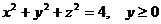 
.
10.11. Пользуясь формулой Гаусса-Остроградского и переходом к цилиндрическим координатам вычислить поверхностный интеграл второго рода 
, где S есть внешняя сторона поверхности конуса 
.
10.12. Пользуясь формулой Гаусса-Остроградского преобразовать поверхностный интеграл второго рода к тройному интегралу по объему V.
10.13. Пользуясь формулой Гаусса-Остроградского преобразовать поверхностный интеграл первого рода 
, где 
непрерывны со своими частными производными,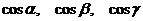 
направляющие косинусы нормали к поверхности S, к тройному интегралу по объему V.
10.14. Пользуясь формулой Гаусса-Остроградского преобразовать поверхностный интеграл второго рода 
к тройному интегралу по объему V.
10.15. Пользуясь формулой Гаусса-Остроградского преобразовать поверхностный интеграл второго рода 
к тройному интегралу по объему V.
10.16. Вычислить поверхностный интеграл второго рода 
, где S есть внешняя сторона поверхности цилиндра 
.
10.17. Пользуясь формулой Стокса вычислить криволинейный интеграл второго рода 
, где L есть окружность, определяющаяся соотношениями 
.
10.18. Пользуясь формулой Стокса вычислить криволинейный интеграл второго рода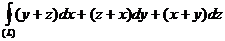 
, где L есть эллипс 
.
10.19. Пользуясь формулой Стокса вычислить криволинейный интеграл второго рода 
, где L есть замкнутая кривая 
, пробегаемая в направлении возрастания t.
10.20. Пользуясь формулой Стокса вычислить криволинейный интеграл второго рода
, где L есть линия пересечения поверхности куба 
плоскостью 
, пробегаемая против хода часовой стрелки, если смотреть с положительной стороны оси ОХ.
10.21. Найти модуль и направление grad U в точке М(-9; 12; 10), если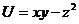 
.
10.22. Пусть 
. Вычислить: 
.
10.23. Найти 
в точке М(3;4;5), если 
.
10.24. Вычислить приближенно поток П вектора через бесконечно малую сферу радиуса e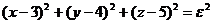 
.
10.25. Найти div (grad U(x, y, z)).
10.26. Доказать тождество 
.
10.27. Найти rot (grad U(x, y, z)).
10.28. Найти 
.
10.29. Найти поток П вектора 
через сферу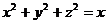 
.
10.30. Найти поток П вектора 
через полную поверхность пирамиды, образованной плоскостями 
10.31. Найти циркуляцию Ц вектора 
вдоль окружности 
.
10.32. Найти циркуляцию Ц вектора вдоль окружности 
.
10.33. Найти циркуляцию Ц вектора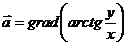 
вдоль контура L, если он окружает ось OZ.
10.34. Найти циркуляцию Ц вектора 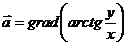вдоль контура L, если он не окружает ось OZ.
10.35. Найти 
, где 
.
Ответы
10.1. 8p. 10.2. 
. 10.3. 
. 10.4. 
. 10.5. 
. 10.6. 108p. 10.7. 0.
10.8.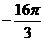 
. 10.9. 0. 10.10. 
. 10.11. 
. 10.12.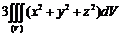 
. 10.13. 0. 10.14. 0.
10.15. 
. 10.16. 36p. 10.17. 
. 10.18. 0. 10.19. 0. 10.20. 
. 10.21. 
. 10.22. 
. 10.23. 
. 10.24. 
. 10.25.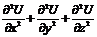 
. 10.27. 0. 10.28. 0. 10.29. 
. 10.30. 0. 10.31. 2p. 10.32. 2p.
10.33. 2p п, п – число оборотов при обходе оси OZ. 10.34. 0.
10.35. 
.
