Примеры
8.1. Вычислить тройной интеграл  , где V есть прямоугольный параллелепипед
, где V есть прямоугольный параллелепипед
 .
.
8.2. Вычислить тройной интеграл  , где область V есть прямоугольный параллелепипед
, где область V есть прямоугольный параллелепипед  .
.
8.3. Вычислить тройной интеграл  , где V есть прямоугольный параллелепипед
, где V есть прямоугольный параллелепипед  .
.
8.4. Вычислить тройной интеграл  , где область V определяется неравенствами
, где область V определяется неравенствами
 .
.
8.5. Вычислить тройной интеграл  , где область V определяется неравенствами
, где область V определяется неравенствами  .
.
8.6. Вычислить тройной интеграл  , где V есть область, ограниченная цилиндром
, где V есть область, ограниченная цилиндром  и плоскостями
и плоскостями  .
.
8.7. Вычислить тройной интеграл  , где V есть область, ограниченная плоскостями
, где V есть область, ограниченная плоскостями  .
.
8.8. Вычислить тройной интеграл  , где V есть область, ограниченная поверхностями
, где V есть область, ограниченная поверхностями  .
.
8.9. С помощью перехода к цилиндрическим координатам вычислить тройной интеграл  , где область V определяется неравенствами
, где область V определяется неравенствами
 .
.
8.10. С помощью перехода к цилиндрическим координатам вычислить тройной интеграл  , где область V определяется неравенствами
, где область V определяется неравенствами
 .
.
8.11. Вычислить тройной интеграл  , где область V есть эллипсоид
, где область V есть эллипсоид  .
.
8.12. С помощью перехода к цилиндрическим координатам вычислить тройной интеграл
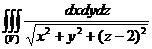 , где область V определяется неравенствами
, где область V определяется неравенствами  .
.
8.13. С помощью перехода к цилиндрическим координатам вычислить тройной интеграл
 , где область V ограничена поверхностями
, где область V ограничена поверхностями  .
.
8.14. С помощью перехода к сферическим координатам вычислить тройной интеграл
 .
.
8.15. С помощью перехода к сферическим координатам вычислить тройной интеграл
 , где область V ограничена шаровой поверхностью
, где область V ограничена шаровой поверхностью 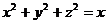 .
.
8.16. С помощью перехода к сферическим координатам вычислить тройной интеграл
 , где область V есть шар
, где область V есть шар 
8.17. С помощью тройного интеграла и с переходом к сферическим координатам вычислить объем шара  .
.
8.18. С помощью тройного интеграла и с переходом к цилиндрическим координатам вычислить объем тела, ограниченного поверхностями  .
.
8.19. С помощью тройного интеграла найти объем тела, ограниченного поверхностями
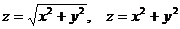 .
.
8.20. С помощью тройного интеграла и с переходом к цилиндрическим координатам вычислить объем тела, ограниченного сферой  и параболоидом
и параболоидом  .
.
8.21. С помощью тройного интеграла вычислить объем тела, ограниченного параболоидом  и конусом
и конусом  .
.
8.22. С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями  , и
, и  .
.
8.23. С помощью тройного интеграла и с переходом к сферическим координатам вычислить объем тела, ограниченного поверхностью  .
.
8.24. С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями  , и
, и  .
.
8.25. С помощью тройного интеграла и с переходом к сферическим координатам вычислить объем тела, ограниченного поверхностью  .
.
Ответы
8.1. 6. 8.2. 18. 8.3. 3080. 8.4.  . 8.5.
. 8.5.  . 8.6.
. 8.6.  . 8.7.
. 8.7.  . 8.8.
. 8.8.  . 8.9.
. 8.9.  . 8.10.
. 8.10.  . 8.11.
. 8.11.  . 8.12.
. 8.12.  . 8.13.
. 8.13.  . 8.14.
. 8.14.  .
.
8.15. 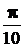 . 8.16.
. 8.16.  . 8.17.
. 8.17.  . 8.18.
. 8.18.  . 8.19.
. 8.19.  . 8.20.
. 8.20.  и
и  . 8.21.
. 8.21.  . 8.22.
. 8.22. 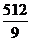 . 8.23.
. 8.23.  . 8.24.
. 8.24.  . 8.25.
. 8.25.  .
.
Раздел IX. Криволинейные интегралы
Примеры
9.1. Вычислить криволинейный интеграл первого рода  , где L – отрезок прямой от А(0;0) до В(4;3).
, где L – отрезок прямой от А(0;0) до В(4;3).
9.2. Вычислить криволинейный интеграл первого рода 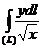 , где L – дуга полукубической параболы
, где L – дуга полукубической параболы 
9.3. Вычислить криволинейный интеграл первого рода  , где L –первая арка циклоиды
, где L –первая арка циклоиды  .
.
9.4. Вычислить криволинейный интеграл первого рода  , где L – правый лепесток лемнискаты Бернулли
, где L – правый лепесток лемнискаты Бернулли  .
.
9.5. Вычислить криволинейный интеграл первого рода 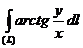 , где L – часть спирали Архимеда
, где L – часть спирали Архимеда  , заключенная внутри круга радиуса
, заключенная внутри круга радиуса 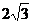 с центром в полюсе.
с центром в полюсе.
9.6. Вычислить криволинейный интеграл первого рода  , где L – эллипс
, где L – эллипс
 .
.
9.7. Вычислить криволинейный интеграл первого рода  , где L – окружность
, где L – окружность 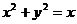 .
.
9.8. Вычислить криволинейный интеграл первого рода  , где L – дуга логарифмической спирали
, где L – дуга логарифмической спирали  .
.
9.9. Вычислить криволинейный интеграл второго рода  , где L – отрезок прямой от точки А(1;1) до точки В(3;4).
, где L – отрезок прямой от точки А(1;1) до точки В(3;4).
9.10. Вычислить криволинейный интеграл второго рода  , где L – контур треугольника с вершинами А(1;2), В(3;1), С(2;5), пробегаемый в положительном направлении (против хода часовой стрелки).
, где L – контур треугольника с вершинами А(1;2), В(3;1), С(2;5), пробегаемый в положительном направлении (против хода часовой стрелки).
9.11. Вычислить криволинейный интеграл второго рода  , где L – первая четверть окружности
, где L – первая четверть окружности 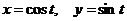 , пробегаемая в положительном направлении (против хода часовой стрелки).
, пробегаемая в положительном направлении (против хода часовой стрелки).
9.12. Вычислить криволинейный интеграл второго рода  , взятый вдоль окружности L:
, взятый вдоль окружности L: 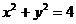 против хода часовой стрелки.
против хода часовой стрелки.
9.13. С помощью формулы Грина вычислить криволинейный интеграл второго рода
 , где L – пробегаемый в положительном направлении контур треугольника с вершинами в точках А(1;1), В(2;2) и С(1;3). Проверить найденный результат, вычисляя интеграл непосредственно.
, где L – пробегаемый в положительном направлении контур треугольника с вершинами в точках А(1;1), В(2;2) и С(1;3). Проверить найденный результат, вычисляя интеграл непосредственно.
9.14. Вычислить криволинейный интеграл второго рода  , где L – дуга параболы
, где L – дуга параболы 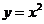 от точки О(0;0) до точки А(1;1).
от точки О(0;0) до точки А(1;1).
9.15. Вычислить криволинейный интеграл второго рода по замкнутому контуру  , где L – окружность
, где L – окружность 
9.16. Вычислить криволинейный интеграл второго рода  ,
,
где L – отрезок прямой от точки А(1;1) до точки В(2;3).
9.17. Пользуясь криволинейным интегралом второго рода, найти функцию  , если
, если
 ,
,
9.18. Пользуясь криволинейным интегралом второго рода, найти функцию  , если
, если

9.19. Пользуясь формулой Грина, вычислить криволинейный интеграл второго рода  , где L – окружность
, где L – окружность  , пробегаемая в положительном направлении.
, пробегаемая в положительном направлении.
9.20. Пользуясь формулой Грина, вычислить криволинейный интеграл второго рода  , где L – окружность
, где L – окружность 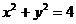 , пробегаемая в положительном направлении.
, пробегаемая в положительном направлении.
9.21. Вычислить криволинейный интеграл второго рода  , где L – отрезок АВ биссектрисы второго координатного угла и абсцисса точки А равна 2 и ордината точки В равна 2.0
, где L – отрезок АВ биссектрисы второго координатного угла и абсцисса точки А равна 2 и ордината точки В равна 2.0
9.22. Вычислить криволинейный интеграл второго рода  , где L – четверть астроиды
, где L – четверть астроиды  от точки А(4;0) до точки В(0;4).
от точки А(4;0) до точки В(0;4).
9.23. Вычислить криволинейный интеграл второго рода  , где L – окружность
, где L – окружность  , пробегаемая в положительном направлении.
, пробегаемая в положительном направлении.
9.24. Вычислить криволинейный интеграл второго рода  , где L – эллипс
, где L – эллипс  , пробегаемый в положительном направлении.
, пробегаемый в положительном направлении.
9.25. Пользуясь криволинейным интегралом второго рода, найти функцию  , если
, если  .
.
9.26. Пользуясь криволинейным интегралом второго рода, найти функцию  , если
, если  .
.
9.27. Вычислить криволинейный интеграл второго рода  , где L – кривая
, где L – кривая  .
.
9.28. Вычислить криволинейный интеграл первого рода  , где L – часть спирали Архимеда
, где L – часть спирали Архимеда 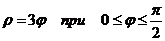 .
.
9.29. Вычислить криволинейный интеграл второго рода  , где L – часть прямой от точки О(0;0) до точки А(2;1).
, где L – часть прямой от точки О(0;0) до точки А(2;1).
9.30. Вычислить криволинейный интеграл второго рода  , где L – часть кривой Гаусса
, где L – часть кривой Гаусса  от точки
от точки  до точки
до точки  .
.
Ответы
9.1.  . 9.2.
. 9.2.  . 9.3.
. 9.3.  . 9.4.
. 9.4.  . 9.5.
. 9.5.  . 9.6.
. 9.6. 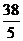 . 9.7.
. 9.7.  .
.
9.8.  . 9.9.
. 9.9.  . 9.10. 17,5. 9.11. p. 9.12. -2p. 9.13.
. 9.10. 17,5. 9.11. p. 9.12. -2p. 9.13.  . 9.14. 1. 9.15. 0. 9.16. 20.5.
. 9.14. 1. 9.15. 0. 9.16. 20.5.
9.17.  .
.
9.18.  . 9.19.
. 9.19.  . 9.20. 4p. 9.21. –2 sin2.
. 9.20. 4p. 9.21. –2 sin2.
9.22.  . 9.23. p. 9.24. 0. 9.25.
. 9.23. p. 9.24. 0. 9.25. 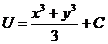 . 9.26.
. 9.26. 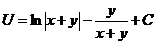 .
.
9.27. 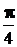 . 9.28.
. 9.28.  . 9.29.
. 9.29.  . 9.30. 0.
. 9.30. 0.






