Примеры
11.1. Пользуясь определением сходимости ряда, найти сумму ряда  .
.
11.2. Пользуясь определением сходимости ряда, найти сумму ряда  .
.
11.3. Пользуясь определением сходимости ряда, найти сумму ряда 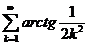 .
.
11.4. Пользуясь определением сходимости ряда, найти сумму ряда 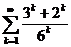 .
.
Исследовать числовые ряды с положительными членами на сходимость
11.5. 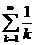 . 11.14.
. 11.14.  .
.
11.6. 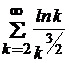 . 11.15.
. 11.15.  .
.
11.7.  . 11.16.
. 11.16. 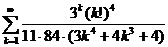 .
.
11.8. 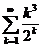 . 11.17.
. 11.17. 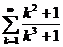 . 11.23.
. 11.23. 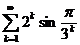 .
.
11.9. 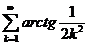 . 11.18.
. 11.18. 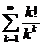 . 11.24.
. 11.24. 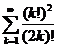 .
.
11.10.  . 11.19.
. 11.19. 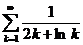 . 11.25.
. 11.25. 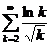 .
.
11.11.  . 11.20.
. 11.20.  .
.
11.12. 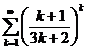 . 11.21.
. 11.21. 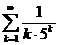 .
.
11.13. 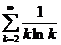 . 11.22.
. 11.22.  .
.
Исследовать числовые ряды с произвольными членами на абсолютную и условную сходимость.
11.26.  . 11.36.
. 11.36.  .
.
11.27.  . 11.37.
. 11.37.  .
.
11.28.  . 11.38.
. 11.38.  .
.
11.29. 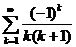 . 11.39.
. 11.39. 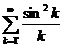 .
.
11.30.  . 11.40.
. 11.40. 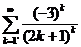 .
.
11.31.  . 11.41.
. 11.41. 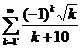 .
.
11.32. 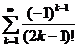 . 11.42.
. 11.42. 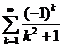 .
.
11.33. 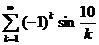 . 11.43.
. 11.43.  .
.
11.34. 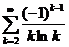 . 11.44.
. 11.44. 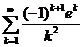 .
.
11.35. 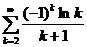 . 11.45.
. 11.45.  .
.
11.46. Дан ряд  . Оценить ошибку, допускаемую при замене суммы этого ряда суммой первых его четырех членов и суммой его пяти членов. Что можно сказать о знаках этих ошибок?
. Оценить ошибку, допускаемую при замене суммы этого ряда суммой первых его четырех членов и суммой его пяти членов. Что можно сказать о знаках этих ошибок?
11.47. Оценить ошибку, допускаемую при замене суммы ряда 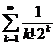 суммой его первых трех членов.
суммой его первых трех членов.
11.48. Оценить ошибку, допускаемую при замене суммы ряда  суммой его первых 10 членов.
суммой его первых 10 членов.
11.49. Сколько членов ряда  нужно взять, чтобы вычислить его сумму с точностью до 0.01; до 0.001?
нужно взять, чтобы вычислить его сумму с точностью до 0.01; до 0.001?
Найти область сходимости следующих функциональных рядов
11.50. 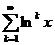 . 11.56.
. 11.56.  .
.
11.51.  . 11.57.
. 11.57.  .
.
11.52. 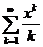 . 11.58.
. 11.58.  .
.
11.53. 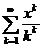 . 11.59.
. 11.59. 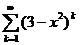 .
.
11.54.  . 11.60.
. 11.60.  .
.
11.55. 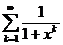 .
.
Доказать равномерную сходимость следующих функциональных рядов в указанных промежутках
11.61. 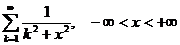 .
.
11.62. 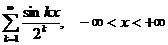 .
.
11.63. 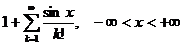 .
.
11.64.  .
.
11.65.  .
.
11.66.  .
.
Найти область равномерной сходимости следующих функциональных рядов
11.67.  . 11.71.
. 11.71. 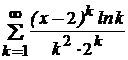 .
.
11.68. 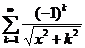 . 11.72.
. 11.72.  .
.
11.69.  . 11.73.
. 11.73. 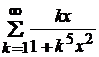 .
.
11.70.  . 11.74.
. 11.74. 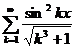 .
.
Найти радиус сходимости и область сходимости следующих степенных рядов
11.75.  . 11.81.
. 11.81. 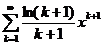 .
.
11.76. 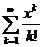 . 11.82.
. 11.82. 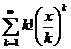 .
.
11.77. 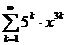 . 11.83.
. 11.83. 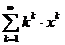 .
.
11.78. 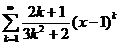 . 11.84.
. 11.84. 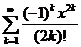 .
.
11.79. 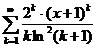 . 11.85.
. 11.85.  .
.
11.80. 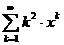 . 11.86.
. 11.86. 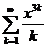 .
.
11.87. Показать, что функция  непрерывна в интервале
непрерывна в интервале  и вычислить
и вычислить 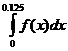 .
.
11.88. Показать, что функция 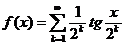 непрерывна на сегменте
непрерывна на сегменте  и вычислить интеграл
и вычислить интеграл  .
.
11.89. Доказать, что функция  при x>0 бесконечно дифференцируема.
при x>0 бесконечно дифференцируема.
11.90. Показать, что ряд  сходится равномерно на
сходится равномерно на 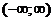 , но его нельзя почленно дифференцировать ни в каком промежутке.
, но его нельзя почленно дифференцировать ни в каком промежутке.
11.91. Для каких х функциональный ряд 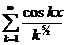 можно почленно дифференцировать?
можно почленно дифференцировать?
11.92. Для каких х функциональный ряд 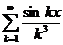 можно почленно дифференцировать?
можно почленно дифференцировать?
11.93. Для каких х функциональный ряд 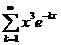 можно почленно дифференцировать?
можно почленно дифференцировать?
Применяя почленное дифференцирование и интегрирование, вычислить суммы следующих рядов.
11.94.  . 11.95.
. 11.95. 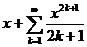 .
.
11.96. 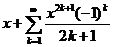 . 11.97.
. 11.97.  .
.
11.98.  . 11.99.
. 11.99.  .
.
11.100. 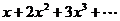 . 11.101.
. 11.101. 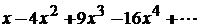 .
.
11.102. 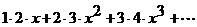 . 11.103.
. 11.103. 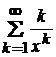 .
.
11.104. Вычислить 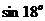 с точностью до
с точностью до 
11.105. Вычислить  с точностью до
с точностью до 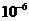
11.106. Вычислить 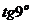 с точностью до
с точностью до 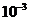
11.107. Вычислить е с точностью до 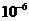
Разложить в ряд Тейлора по степеням х следующие функции и указать области их сходимости
11.108. 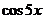 . 11.115.
. 11.115.  .
.
11.109. 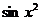 . 11.116. shx.
. 11.116. shx.
11.110.  . 11.117.
. 11.117.  .
.
11.111. 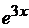 . 11.118.
. 11.118. 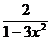 .
.
11.112. 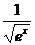 . 11.119.
. 11.119.  .
.
11.113.  . 11.120.
. 11.120. 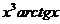 .
.
11.114. 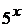 . 11.121.
. 11.121. 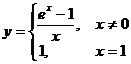 .
.
11.122. 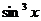 .
.
Ответы
11.1.  . 11.26. Сходится условно
. 11.26. Сходится условно
11.2. 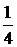 . 11.27. Сходится условно
. 11.27. Сходится условно
11.3. 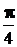 11.28. Расходится
11.28. Расходится
11.4. 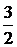 11.29. Сходится абсолютно
11.29. Сходится абсолютно
11.5. Расходится 11.30. Расходится
11.6. Сходится 11.31. Сходится абсолютно
11.7. Сходится 11.32. Сходится абсолютно
11.8. Сходится 11.33. Сходится условно
11.9. Сходится 11.34. Сходится условно
11.10. Расходится 11.35. Сходится условно
11.11. Сходится 11.36. Сходится условно
11.12. Сходится 11.37. Сходится условно
11.13. Расходится 11.38. Сходится условно
11.14. Сходится. Указание:
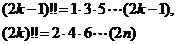 11.39. Расходится
11.39. Расходится
11.15. Расходится 11.16. Сходится. Указание: применить признак Раабе
11.17. Расходится 11.42. Сходится абсолютно
11.18. Сходится 11.43. Расходится
11.19. Расходится 11.44. Расходится
11.20. Сходится 11.45. Сходится абсолютно
11.21. Сходится 11.40. Сходится абсолютно
11.22. Сходится 11.41. Сходится условно.
11.23. Сходится
11.24. Сходится
11.25. Расходится
11.46. 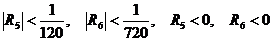 . 11.47.
. 11.47. 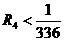 . 11.48.
. 11.48. 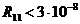 .
.
11.49. 99; 999. 11.50. 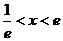 .
.
11.51. x>0 11.83. R=0, x=0
11.52. 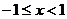 11.84.
11.84. 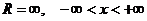
11.53.  11.85.
11.85. 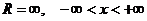
11.54.  11.86.
11.86. 
11.55. 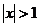 11.87.
11.87. 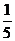
11.56. 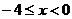 11.88.
11.88. 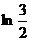
11.57.  11.91.
11.91. 
11.58.  11.92.
11.92. 
11.59. 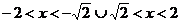 11.93.
11.93. 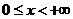
11.60. 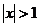 11.94.
11.94. 
11.67.  11.95.
11.95. 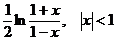
11.68.  11.96.
11.96. 
11.69. 0<x<1 11.97. 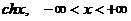
11.70. 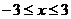 11.98.
11.98. 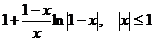
11.71. 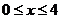 11.99.
11.99. 
11.72. 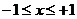 11.100.
11.100. 
11.73. 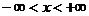 11.101.
11.101. 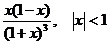
11.74.  11.102.
11.102. 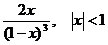
11.75.  11.103.
11.103. 
11.76. 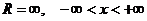 11.104. 0.30902
11.104. 0.30902
11.77. 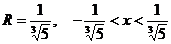 11.105. 0.999848
11.105. 0.999848
11.78. 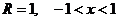 11.106. 0.158
11.106. 0.158
11.79.  11.107. 2.718282
11.107. 2.718282
11.80. 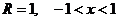
11.81.  . 11.82.
. 11.82.  .
.
11.108. 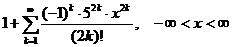 . 11.109.
. 11.109. 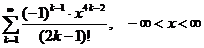 .
.
11.110. 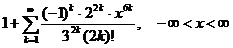 . 11.111.
. 11.111. 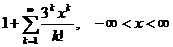 .
.
11.112. 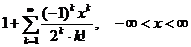 . 11.113.
. 11.113.  .
.
11.114. 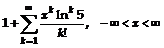 . 11.115.
. 11.115. 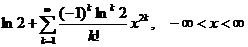 .
.
11.116. 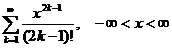 . 11.117.
. 11.117. 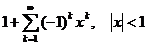 .
.
11.118. 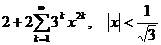 . 11.119.
. 11.119.  .
.
11.120. 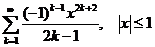 . 11.121.
. 11.121. 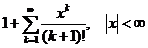 .
.
11.122.  .
.
Раздел XII. Ряды Фурье
Примеры




