Примеры
7.1. Вычислить двойной интеграл  , где область D есть прямоугольник
, где область D есть прямоугольник
 .
.
7.2. Вычислить двойной интеграл  , где область D есть квадрат
, где область D есть квадрат
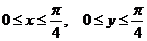 .
.
7.3. Вычислить двойной интеграл  , где область D есть прямоугольник
, где область D есть прямоугольник
 .
.
7.4. Вычислить двойной интеграл 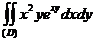 , где область D есть прямоугольник
, где область D есть прямоугольник
 .
.
7.5. Вычислить двойной интеграл  , где область D есть квадрат
, где область D есть квадрат
 .
.
7.6. Изменить порядок интегрирования в интеграле 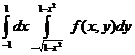 .
.
7.7. Изменить порядок интегрирования в интеграле  .
.
7.8. Изменить порядок интегрирования в интеграле  .
.
7.9. Изменить порядок интегрирования в интеграле  .
.
7.10. Изменить порядок интегрирования в интеграле  .
.
7.11. Вычислить двойной интеграл 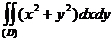 , где D есть область, ограниченная линиями
, где D есть область, ограниченная линиями  .
.
7.12. Вычислить двойной интеграл  , где D есть часть области в первом квадранте, ограниченная эллипсом
, где D есть часть области в первом квадранте, ограниченная эллипсом  .
.
7.13. Вычислить двойной интеграл  , где D есть область, ограниченная линией
, где D есть область, ограниченная линией 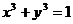 и осями координат.
и осями координат.
7.14. Вычислить двойной интеграл  , где D есть область, ограниченная линиями
, где D есть область, ограниченная линиями  .
.
7.15. Вычислить двойной интеграл  , де D есть область, ограниченная линиями
, де D есть область, ограниченная линиями  .
.
7.16. Вычислить двойной интеграл  , где D есть область, ограниченная параболой
, где D есть область, ограниченная параболой  и прямой х = 1.
и прямой х = 1.
7.17. Вычислить двойной интеграл  , где D есть область, ограниченная осью абсцисс и первой аркой циклоиды
, где D есть область, ограниченная осью абсцисс и первой аркой циклоиды  .
.
7.18. С переходом к полярным координатам, вычислить двойной интеграл 
 , где D есть область
, где D есть область  .
.
7.19. С переходом к полярным координатам, вычислить двойной интеграл 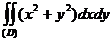 , где D есть область, ограниченная окружностью
, где D есть область, ограниченная окружностью  .
.
7.20. С переходом к обобщенным полярным координатам  по формулам
по формулам
 вычислить двойной интеграл
вычислить двойной интеграл  , где D есть область, ограниченная эллипсом
, где D есть область, ограниченная эллипсом 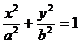 .
.
7.21. С переходом к новым переменным по формулам  вычислить двойной интеграл
вычислить двойной интеграл  , где область D есть квадрат, ограниченный прямыми
, где область D есть квадрат, ограниченный прямыми  .
.
7.22. С переходом к новым переменным по формулам  вычислить двойной интеграл
вычислить двойной интеграл  , где область D ограничена линиями
, где область D ограничена линиями
 .
.
7.23. С помощью двойного интеграла вычислить площадь, ограниченную линиями  .
.
7.24. С помощью двойного интеграла и с переходом к полярным координатам вычислить площадь фигуры, ограниченной лемнискатой  .
.
7.25. С помощью двойного интеграла вычислить площадь фигуры, ограниченную линиями
 .
.
7.26. С помощью двойного интеграла и с переходом к полярным координатам вычислить площадь фигуры, ограниченной линией  .
.
7.27. С помощью двойного интеграла и с переходом к новым переменным по формулам  вычислить площадь фигуры, ограниченной эллипсом
вычислить площадь фигуры, ограниченной эллипсом
 .
.
7.28. С помощью двойного интеграла вычислить объем тела, ограниченного поверхностями  .
.
7.29. С помощью двойного интеграла вычислить объем тела, ограниченного параболоидами  , цилиндром
, цилиндром 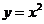 и плоскостью
и плоскостью  .
.
7.30. С помощью двойного интеграла вычислить объем тела, ограниченного цилиндром  , параболоидом
, параболоидом  и плоскостью
и плоскостью  .
.
7.31. С помощью двойного интеграла вычислить объем тела, ограниченного эллиптическим параболоидом  и плоскостями
и плоскостями  .
.
7.32. С помощью двойного интеграла и с переходом к цилиндрическим координатам вычислить объем тела, ограниченного поверхностями  .
.
7.33. С помощью двойного интеграла вычислить объем тела, ограниченного плоскостью  , цилиндром
, цилиндром  и конусом
и конусом  .
.
7.34. С помощью двойного интеграла и с переходом к новым переменным по формулам  и
и  вычислить объем тела, ограниченного поверхностями
вычислить объем тела, ограниченного поверхностями
 .
.
7.35. С помощью двойного интеграла вычислить объем тела, ограниченного поверхностями  .
.
Ответы
7.1. 8. 7.2. ≈  0,6. 7.3.
0,6. 7.3. 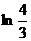 . 7.4.
. 7.4.  . 7.5. 1. 7.6.
. 7.5. 1. 7.6.  .
.
7.7.  . 7.8.
. 7.8. 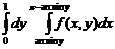 . 7.9.
. 7.9.  .
.
7.10. 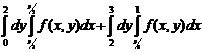 . 7.11.
. 7.11.  . 7.12. 4,5. 7.13.
. 7.12. 4,5. 7.13.  . 7.14.
. 7.14.  .
.
7.15. 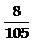 . 7.16.
. 7.16. 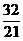 . 7.17.
. 7.17. 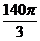 . 7.18.
. 7.18.  . 7.19.
. 7.19.  . 7.20.
. 7.20.  . 7.21.
. 7.21.  . 7.22.
. 7.22.  . 7.23. 5. 7.24. 1. 7.25.
. 7.23. 5. 7.24. 1. 7.25.  . 7.26.
. 7.26.  . 7.27. 10
. 7.27. 10  . 7.28.
. 7.28. 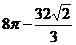 . 7.29.
. 7.29. 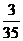 . 7.30.
. 7.30.  .
.
7.31.  . 7.32.
. 7.32.  . 7.33.
. 7.33. 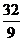 . 7.34.
. 7.34.  . 7.35.
. 7.35.  .
.






