Примеры
Вычислить следующие определенные интегралы.
5.1.  . 5.2.
. 5.2.  .
.
5.3.  . 5.4.
. 5.4.  .
.
5.5.  . 5.6.
. 5.6. 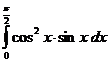 .
.
5.7.  . 5.8.
. 5.8.  .
.
5.9.  . 5.10.
. 5.10.  .
.
5.11. 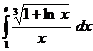 . 5.12.
. 5.12.  .
.
5.13.  . 5.14.
. 5.14.  .
.
5.15.  . 5.16.
. 5.16.  .
.
5.17.  . 5.18.
. 5.18.  .
.
5.19.  . 5.20.
. 5.20.  .
.
5.21. Вычислить площадь фигуры, ограниченной следующими линиями:
1). осями координат, прямой x = 3 и параболой y=x2+1;
2). осью ординат, прямыми y = - 2, y = 3 и параболой 2x = y2;
3). параболами y = x2 + 1,  и прямой y = 5;
и прямой y = 5;
4). параболами y = x2 и x = y2.
5.22. Найти площади двух фигур, ограниченных параболой y2 = 2x
и окружностью y2 = 4x – x2.
5.23. Найти площадь фигуры, ограниченной линией y2 = x (x – 1)2.
5.24. Вычислить площадь фигуры, ограниченной параболой
y = - x2 + 6x – 5 и осями координат.
5.25. Вычислить площадь фигуры, ограниченной следующими линиями:
1). окружностью x2 + y2 = R2;
2). одной полуволной синусоиды y = sin x и осью Оx;
3). гиперболой y·x = 7 и прямыми x = 2, x = 7, y = 0;
4). кривой y = ln x и прямыми x = e, y = 0;
5). параболой y = 4 – x2 и осью абсцисс;
6). полукубической параболой y2 = x3, осью ординат и прямой y = 2;
7). линией  и прямыми x = - a, x = a (a>0);
и прямыми x = - a, x = a (a>0);
8). кубической параболой y = x3, прямой y = 2 и осью Оy;
9). кривыми y = ex, y = e-x и прямой y = 4;
10). эллипсом  (a>0, b>0);
(a>0, b>0);
11). Линиями y = x2 и  .
.
5.26. Вычислить площадь фигуры между смежными наибольшим и наименьшим радиусами-векторами каждой кривой:
1).  ;
;
2).  ;
;
3).  ;
;
4).  .
.
5.27. Вычислить длину окружности x2 + y2 = R2 (R>0).
5.28. Найти длину астроиды  (a>0).
(a>0).
5.29. Вычислить длину дуги параболы y2 = 4x от вершины до точки M (1; 2).
Вычислить длину дуги кривой:
5.30.  между прямыми
между прямыми  (a>0).
(a>0).
5.31.  от x = 0,75 до x = 2,4.
от x = 0,75 до x = 2,4.
5.32. y = ln (2 cos x) между смежными точками пересечения о осями координат Оy и Оx.
5.33. Кардиоиды  (a>0).
(a>0).
5.34. Первого завитка спирали Архимеда  (a>0).
(a>0).
5.35. Всей кривой  .
.
5.36. y2 = 2px, отсеченной прямой  (p>0).
(p>0).
5.37. Эллипс  a > b вращается: 1). вокруг большой оси; 2). вокруг малой оси. Найти объемы получающихся эллипсоидов вращения.
a > b вращается: 1). вокруг большой оси; 2). вокруг малой оси. Найти объемы получающихся эллипсоидов вращения.
5.38. Определить объем тела, образованного вращением фигуры, ограниченной линиями:
1).  ;
;
2).  ;
;
3).  ;
;
4).  ;
;
5).  (a>0);
(a>0);
6).  (b>0, R>0);
(b>0, R>0);
7).  (a>0).
(a>0).
5.39. Определить площадь поверхности, образованной вращением кривой:
1).  (R>0);
(R>0);
2). y = 0,5 x2, отсеченной прямой y = 1,5, вокруг оси Оy;
3).  ;
;
4). Одной полуволновой кривой y = sin x вокруг оси Оx;
5). Одной арки циклоиды  вокруг оси Оx (a>0);
вокруг оси Оx (a>0);
6).  (b>0, R>0);
(b>0, R>0);
7). 
8). Всей кривой x = a cos3 t, y = a sin3 t (a>0);
9).  (a>0, b>0).
(a>0, b>0).
Ответы
5.1.  . 5.2.
. 5.2. 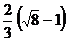 . 5.3.
. 5.3.  . 5.4.
. 5.4.  . 5.5. e2.. 5.6. 0,25. 5.7. – 1. 5.8.
. 5.5. e2.. 5.6. 0,25. 5.7. – 1. 5.8.  . 5.9.
. 5.9.  . 5.10.
. 5.10.  . 5.11.
. 5.11.  . 5.12.
. 5.12.  . 5.13.
. 5.13.  .
.
5.14.  . 5.15.
. 5.15.  . 5.16.
. 5.16.  . 5.17.
. 5.17.  . 5.18.
. 5.18.  .
.
5.19.  . 5.20.
. 5.20. 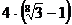 . 5.21. 1) 12; 2)
. 5.21. 1) 12; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
5.22.  . 5.23.
. 5.23.  . 5.24. 13.
. 5.24. 13.
5.25. 1)  R2; 2) 2; 3) 7 ln 2,5; 4) 1; 5)
R2; 2) 2; 3) 7 ln 2,5; 4) 1; 5) 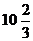 ; 6)
; 6)  ; 7)
; 7)  ; 8).
; 8).  ;
;
9)  ; 10) Пab; 11)
; 10) Пab; 11)  . 5.26. 1).
. 5.26. 1).  ; 2).
; 2).  ; 3).
; 3).  ; 4).
; 4).  .
.
5.27. 2  R. 5.28. 6a. 5.29.
R. 5.28. 6a. 5.29. 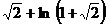 . 5.30. 2a sh1. 5.31. 1,35 + ln 2.
. 5.30. 2a sh1. 5.31. 1,35 + ln 2.
5.32.  . 5.33. 8a. 5.34.
. 5.33. 8a. 5.34.  . 5.35.
. 5.35. 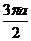 .
.
5.36.  . 5.37. 1).
. 5.37. 1).  ; 2).
; 2).  .
.
5.38. 1)  ph2; 2) 8
ph2; 2) 8  ; 3) 64
; 3) 64  ; 58,5
; 58,5  ; 4)
; 4)  ; 5)
; 5)  ; 6) 2
; 6) 2  2 R2 b; 7)
2 R2 b; 7)  .
.
5.39. 1). 4  R2; 2).
R2; 2).  ; 3).
; 3).  ; 4).
; 4).  ; 5).
; 5).  ;
;
6). 4  2 bR; 7).
2 bR; 7).  ; 8). 2,4
; 8). 2,4  a2;
a2;
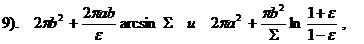

Раздел VI. Несобственные интегралы.
Примеры
6.1. Вычислить несобственный интеграл первого рода  .
.
6.2. Вычислить несобственный интеграл первого рода  .
.
6.3. Вычислить несобственный интеграл первого рода  .
.
6.4. Вычислить несобственный интеграл первого рода  .
.
6.5. Вычислить несобственный интеграл первого рода 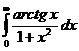 .
.
6.6. Вычислить несобственный интеграл первого рода  .
.
6.7. Вычислить несобственный интеграл первого рода 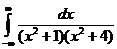 .
.
6.8. Вычислить несобственный интеграл первого рода  .
.
6.9. Вычислить несобственный интеграл первого рода 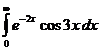 .
.
6.10. Вычислить несобственный интеграл первого рода в смысле главного значения
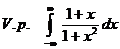 .
.
6.11. Вычислить несобственный интеграл второго рода  .
.
6.12. Вычислить несобственный интеграл второго рода 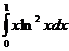 .
.
6.13. Вычислить несобственный интеграл второго рода  .
.
6.14. Вычислить несобственный интеграл второго рода  .
.
6.15. Вычислить несобственный интеграл второго рода  .
.
6.16. Вычислить несобственный интеграл второго рода  .
.
6.17. Вычислить несобственный интеграл второго рода 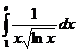 .
.
6.18. Вычислить несобственный интеграл второго рода  .
.
6.19. Вычислить несобственный интеграл второго рода  .
.
6.20. Вычислить несобственный интеграл второго рода в смысле главного значения
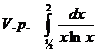 .
.
6.21. Исследовать сходимость несобственного интеграла первого рода  .
.
6.22. Исследовать сходимость несобственного интеграла первого рода  .
.
6.23. Исследовать сходимость несобственного интеграла первого рода  .
.
6.24. Вычислить несобственный интеграл первого рода  , пользуясь интегралом Пуассона
, пользуясь интегралом Пуассона  .
.
6.25. Вычислить несобственный интеграл первого рода  , пользуясь интегралом Дирихле
, пользуясь интегралом Дирихле  .
.
6.26. Исследовать сходимость несобственного интеграла второго рода  .
.
6.27. Исследовать сходимость несобственного интеграла второго рода  .
.
6.28. Исследовать сходимость несобственного интеграла второго рода 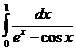 .
.
6.29. При каких значениях т несобственный интеграл второго рода  .
.
сходится, при каких – расходится.
6.30. Исследовать сходимость несобственного интеграла второго рода
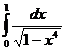 .
.
Ответы
6.1. 1. 6.2.  . 6.3. ¥. 6.4.
. 6.3. ¥. 6.4.  . 6.5.
. 6.5.  . 6.6.
. 6.6. 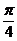 . 6.7.
. 6.7.  . 6.8.
. 6.8.  . 6.9.
. 6.9.  . 6.10. p. 6.11. ¥. 6.12.
. 6.10. p. 6.11. ¥. 6.12.  . 6.13. 2. 6.14. p. 6.15.
. 6.13. 2. 6.14. p. 6.15.  . 6.16.
. 6.16.  . 6.17. 2. 6.18.
. 6.17. 2. 6.18.  . 6.19.
. 6.19.  . 6.20. 0.
. 6.20. 0.
6.21. Расходится. 6.22. Сходится. 6.23. Сходится. 6.24.  . 6.25.
. 6.25.  . 6.26. Сходится. 6.27. Расходится. 6.28. Расходится. 6.29. При m <3 сходится, при
. 6.26. Сходится. 6.27. Расходится. 6.28. Расходится. 6.29. При m <3 сходится, при  расходится. 6.30. Сходится.
расходится. 6.30. Сходится.






