Математика. Математический анализ
Сборник задач
 |
Раздел I. Теория последовательностей и функций одной переменной
Примеры
1.1. Доказать, что последовательность  является бесконечно большой.
является бесконечно большой.
1.2. Доказать, что последовательность  является бесконечно малой.
является бесконечно малой.
1.3. Доказать, что предел последовательности  равен 1.
равен 1.
1.4. Доказать, что  .
.
1.5. Доказать, что  . По данному числу
. По данному числу  найти наибольшее число
найти наибольшее число  такое, чтобы при любом х из d – окрестности числа 3 значение функции (2х-1) оказалось в e – окрестности числа 3.
такое, чтобы при любом х из d – окрестности числа 3 значение функции (2х-1) оказалось в e – окрестности числа 3.
Найти пределы:
1.6.  . 1.7.
. 1.7.  .
.
1.8.  . 1.9.
. 1.9.  .
.
1.10.  . 1.11.
. 1.11.  .
.
1.12.  . 1.13.
. 1.13.  .
.
1.14.  . 1.15.
. 1.15.  .
.
1.16. 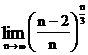 . 1.17.
. 1.17.  .
.
1.18.  . 1.19.
. 1.19.  .
.
1.20.  1.21.
1.21.  .
.
1.22.  . 1.23.
. 1.23.  .
.
1.24.  . 1.25.
. 1.25.  .
.
1.26.  . 1.27.
. 1.27.  ..
..
1.28.  . 1.29.
. 1.29.  .
.
1.30.  . 1.31.
. 1.31. 
1.32.  . 1.33.
. 1.33.  .
.
1.34.  . 1.35.
. 1.35.  .
.
1.36.  . 1.37.
. 1.37.  .
.
1.38.  . 1.39.
. 1.39. 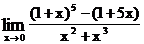
1.40.  1.41.
1.41.  .
.
1.42.  1.43.
1.43. 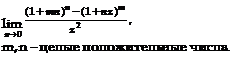
1.44.  . 1.45.
. 1.45. 
1.46.  . 1.47.
. 1.47.  .
.
1.48.  . 1.49.
. 1.49.  .
.
1.50.  . 1.51.
. 1.51.  .
.
1.52.  . 1.53.
. 1.53.  , n – целое полож. число.
, n – целое полож. число.
1.54.  . 1.55.
. 1.55.  .
.
1.56.  . 1.57.
. 1.57.  .
.
1.58.  . 1.59.
. 1.59. 
1.60.  . 1.61.
. 1.61.  .
.
1.62.  . 1.63.
. 1.63.  .
.
1.64. а)  ; 1.65.
; 1.65.  .
.
б)  ;
;
в) 
1.66.  . 1.67.
. 1.67.  .
.
1.68.  . 1.69.
. 1.69.  .
.
1.70. 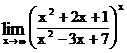 . 1.71.
. 1.71.  .
.
1.72. 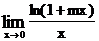 . 1.73.
. 1.73. 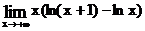 .
.
1.74. 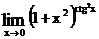 . 1.75.
. 1.75. 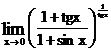 .
.
1.76.  . 1.77.
. 1.77.  .
.
1.78.  . 1.79.
. 1.79.  .
.
1.80.  .
.
1.81. Определить порядки бесконечно малых:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8) 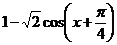
относительно бесконечно малой х.
1.82. Доказать, что при 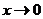 :
:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ; 7)
; 7)  ,
,
где» – означает знак эквивалентности.
1.83. Указать точку разрыва функции  . Найти
. Найти  .
.
1.84. Найти точки разрыва и определить их характер:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ; 7)
; 7)  .
.
1.85. Найти асимптоты кривых:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8) 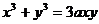 ; 9)
; 9)  ;
;
10) 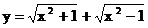 ; 11)
; 11)  ; 12)
; 12) 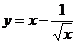 .
.
Ответы
1.6. 0. 1.7. ¥. 1.8. 2. 1.9. –0,6. 1.10.  . 1.11. 0,25. 1.12.
. 1.11. 0,25. 1.12.  . 1.13.
. 1.13.  . 1.14.
. 1.14.  . 1.15. 0. 1.16.
. 1.15. 0. 1.16.  . 1.17. 2. 1.18. 0. 1.19.
. 1.17. 2. 1.18. 0. 1.19.  . 1.20. 0. 1.21. 0. 1.22. 2. 1.23. 0. 1.24. 4. 1.25. 0.
. 1.20. 0. 1.21. 0. 1.22. 2. 1.23. 0. 1.24. 4. 1.25. 0.
1.26. –1. 1.27. 0,75. 1.28. 0. 1.29.  . 1.30. 0,5. 1.31. 0,5. 1.32. 1. 1.33. 3. 1.34. 1. 1.35. 0. 1.36.
. 1.30. 0,5. 1.31. 0,5. 1.32. 1. 1.33. 3. 1.34. 1. 1.35. 0. 1.36.  . 1.37.
. 1.37.  . 1.38. 0,5. 1.39. 10. 1.40. –0,4. 1.41. –1. 1.42.
. 1.38. 0,5. 1.39. 10. 1.40. –0,4. 1.41. –1. 1.42.  . 1.43.
. 1.43.  .
.
1.44. 1. 1.45. ¥. 1.46. 0. 1.47.  . 1.48. 0. 1.49. 0
. 1.48. 0. 1.49. 0  .
.  . 1.50. 1. 1.51. 2. 1.52. 0. 1.53. n. 1.54. 1,5. 1.55. 0,5. 1.56. 0,5. 1.57. –1,5. 1.58. –1. 1.59. –0,5. 1.60.
. 1.50. 1. 1.51. 2. 1.52. 0. 1.53. n. 1.54. 1,5. 1.55. 0,5. 1.56. 0,5. 1.57. –1,5. 1.58. –1. 1.59. –0,5. 1.60.  . 1.61.
. 1.61.  . 1.62.
. 1.62.  . 1.63. 0. 1.64. а) 0,5; б)
. 1.63. 0. 1.64. а) 0,5; б)  ; в) 1. 1.65.
; в) 1. 1.65.  . 1.66. 1. 1.67. 0. 1.68.
. 1.66. 1. 1.67. 0. 1.68.  . 1.69. 0.
. 1.69. 0.
1.70.  . 1.71. е. 1.72. т. 1.73. 1. 1.74. е. 1.75. 1. 1.76. ln a. 1.77. e. 1.78.
. 1.71. е. 1.72. т. 1.73. 1. 1.74. е. 1.75. 1. 1.76. ln a. 1.77. e. 1.78.  . 1.79. 0. 1.80. 1. 1.81. 1) 2-го; 2) 3-го; 3) 1-ого; 4) 1-ого; 5) 3-го; 6) 2-го; 7) 3-го; 8) 2-го. 1.83. х = 3.
. 1.79. 0. 1.80. 1. 1.81. 1) 2-го; 2) 3-го; 3) 1-ого; 4) 1-ого; 5) 3-го; 6) 2-го; 7) 3-го; 8) 2-го. 1.83. х = 3.
 .
.
 .
.
Раздел II. Дифференциальное исчисление функции одной переменной
Примеры
Найти производные от функций:
2.1.  . 2.2.
. 2.2.  .
.
2.3. 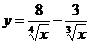 . 2.4.
. 2.4.  .
.
2.5.  . 2.6.
. 2.6.  .
.
2.7. 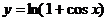 . 2.8.
. 2.8. 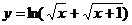 .
.
2.9.  . 2.10.
. 2.10.  .
.
2.11.  . 2.12.
. 2.12.  .
.
2.13.  . 2.14.
. 2.14.  .
.
2.15.  . 2.16.
. 2.16.  .
.
2.17.  . 2.18.
. 2.18.  .
.
2.19.  . 2.20.
. 2.20.  .
.
2.21.  . 2.22.
. 2.22.  .
.
2.23.  . 2.24.
. 2.24.  .
.
2.25.  .
.
2.26. Найти производную 2-ого порядка от функций:
1) 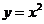 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
2.27. Найти производные от у по х:

2.28. Применить формулу Лейбница для вычисления производной:
1) 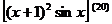 ; 2)
; 2)  ; 3)
; 3)  .
.
Найти интервалы монотонности данных функций:
2.29.  . 2.30.
. 2.30.  .
.
2.31. 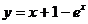 . 2.32.
. 2.32.  .
.
Провести полное исследование функций и построить ее график:
2.33.  . 2.34.
. 2.34.  .
.
2.35.  . 2.36.
. 2.36.  .
.
2.37.  . 2.38.
. 2.38.  .
.
2.39.  . 2.40.
. 2.40.  .
.
2.41.  . 2.42.
. 2.42. 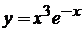 .
.
2.43.  . 2.44.
. 2.44.  .
.
2.45.  . 2.46.
. 2.46.  .
.
2.47.  . 2.48.
. 2.48.  .
.
2.49.  .2.50.
.2.50.  .
.
2.51.  . 2.52.
. 2.52. 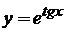 .
.
2.53.  . 2.54.
. 2.54.  .
.
2.55.  .
.
2.56. Найти производные от y по x второго порядка:
1). x=ln t, y=t2-1;
2). x=arcsin t, y=ln (1-t2);
3). x=a ( – sin
– sin  ), y=a (1-cos
), y=a (1-cos  ).
).
2.57. Найти общие выражения для производных порядка n от функций
1). y=eax; 2). y=  3). y=
3). y= 
2.58. Показать, что функция y=ex sin x удовлетворяет соотношению
y''-2y'+2y=0
2.59. Найти дифференциалы второго порядка от функций:
1). y=  ;
;
2). y= 4- x  .
.
2.60. Удовлетворяет ли функция y= 1 -  условиям теоремы Ролля на сегментами [-1; 1].
условиям теоремы Ролля на сегментами [-1; 1].
2.61. Написать формулу Лагранта и найти c для функций:
1). f(x)=x3 на отрезке [а; b];
2). f(x)=arctg x на отрезке [0; 1];
3). f(x)=x2+3 на отрезке [-1; 2];
4). f(x)=arcsin x на отрезке [0; 1];
5). f(x)=ln x на отрезке [1; 2).
2.62. Написать формулу Коши и найти c для функций:
1). sin x и cos x на отрезке [0;  ];
];
2). x2 и  на отрезке [1; 4].
на отрезке [1; 4].
2.63. Написать формулу Коши для функций f(x)=e2x  (x)=1+ex на отрезке [а; b].
(x)=1+ex на отрезке [а; b].
2.64. Найти пределы по правилам Лопиталя.
1).  ; 2).
; 2).  ; 3).
; 3).  ; 4).
; 4). 
5).  ; 6).
; 6).  ; 7).
; 7).  ; 8).
; 8).  ;
;
9).  n>0; 10).
n>0; 10).  ; 11).
; 11).  .
.
2.65. Разложить многочлен x3+2x2+3x+4 по степеням двучлена x-1, пользуясь формулой Тейлора.
2.66. Разложить функцию f(x)=x4-4x2 по степеням x+2, пользуясь формулой Тейлора.
2.67. Найти формулу Маклорена n=20 порядка для функции y=xex.
2.68. Применить формулу Маклорена к функции f(x)= sin x, полагая n=5.
Ответы
2.1. 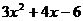 . 2.2.
. 2.2.  . 2.3.
. 2.3.  . 2.4.
. 2.4.  .
.
2.5.  . 2.6.
. 2.6.  .
.
2.7.  . 2.8.
. 2.8.  . 2.9.
. 2.9.  . 2.10.
. 2.10.  . 2.11.
. 2.11.  .
.
2.12.  . 2.13.
. 2.13.  . 2.14. 0.
. 2.14. 0.
2.15.  .
.
2.16.  . 2.17.
. 2.17.  . 2.18.
. 2.18.  .
.
2.19.  . 2.20.
. 2.20.  .
.
2.21.  . 2.22.
. 2.22.  .
.
2.23.  .
.
2.24.  . 2.25.
. 2.25.  .
.
2.26.  .
.
2.27.  .
.

2.29.  .
.
2.30.  .
.
2.31.  . 2.32. монотонно возрастает.
. 2.32. монотонно возрастает.
2.56. 1). 4t2, 2). -  , 3). -
, 3). -  , 2.57. 1). an eax; 2).
, 2.57. 1). an eax; 2).  ;
;
3).  . 2.59. 1).
. 2.59. 1).  ;
;
2). 4 
 .
.
2.60. Нет, так как внутри сегмента имеется точка x=0, в которой производная не существует.
2.61. 1).  ; 2).
; 2).  ; 3).
; 3).  ; 4).
; 4).  ; 5).
; 5).  ;
;
2.62. 1).  ; 2).
; 2). 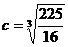 . 2.63. eb+ea=2ec , где a<c<b.
. 2.63. eb+ea=2ec , где a<c<b.
2.64. 1)  ; 2) ln a; 3).
; 2) ln a; 3).  ; 4) 1,5; 5)
; 4) 1,5; 5)  ; 6) 2; 7)
; 6) 2; 7)  ; 8) -
; 8) -  ; 9) 0; 10) 0,5; 11) 0.
; 9) 0; 10) 0,5; 11) 0.
2.65. 10+10 (x-1)+5 (x-1)2+(x-1)3. 2.66. (x+2)4-8 (x+2)3+20 (x+2)2-16 (x+2).
2.67.  , где 0<
, где 0<  <1.
<1.
2.68. 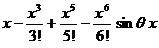 , где 0<
, где 0<  <1.
<1.
Раздел III. Дифференциальное исчисление функции нескольких переменных.
Примеры
3.1. Найти частные производные первого порядка от функций:
1). z=x3+2xy2-y4
2). u=cos2 (x+y)-sin2 x+cos2y
3). z= 
4). z=cos (ax+by), где а=const, b=const
5). z= 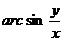
6). z=x ln y+arcsin y
7). z=xy
8). z=(sin x)cos y
3.2. Найти полные дифференциалы функций:
1). z=2x-4y; 2). z=xy ; 3). u=xyz; 4). u=ln (x2-y2).
3.3. Найти частные производные третьего порядка от функции z=x3+x2y+y3.
3.4. Найти производные второго порядка от функции z=  .
.
3.5. Найти d2 z и d3 z от функции z=y ln x.
3.6. Написать уравнения касательной плоскости и нормали к поверхности:
1). z=x2+2y2 в точке (1; 1; 3).
2). x2+y2 = z2 в точке (3; 4; 5)
3.7. Найти углы между нормалью к поверхности
x2+y2-xz-yz=0 в точке М (0; 2; 2) и осями координат.
3.8. Исследовать на экстремум следующие функции:
1).  ; 2).
; 2).  ; 3).
; 3).  ; 4).
; 4).  ;
;
5).  ; 6).
; 6).  ;
;
7).  ; 8).
; 8).  ;
;
9).  (a>0); 10).
(a>0); 10).  ;
;
11).  (a>0);
(a>0);
12).  .
.
3.9. Найти производные  ,
,  от функции
от функции  , если
, если  ,
, 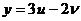 .
.
3.10. Найти производные  ,
,  от функции
от функции  , если
, если  ,
,  .
.
3.11. Найти производную  от функции
от функции  , если
, если  ,
,  .
.
3.12. Дано  . Показать, что функция u(x,y) удовлетворяет соотношению
. Показать, что функция u(x,y) удовлетворяет соотношению  .
.
3.13. Найти grad z от следующих функций:
1).  в точке (3; 2);
в точке (3; 2);
2).  в точке (2; 1);
в точке (2; 1);
3).  в точке (1; 1).
в точке (1; 1).
3.14. Найти производную функции z=ln(x+y) в точке (1; 2), принадлежащей параболе y2=4 x, по направлению этой параболы.
3.15. Найти производную функции z=x3-3x2y+3xy2+1 в точке (3; 1) в направлении, идущем от этой точки к точке (6; 5).
Ответы
3.1. 1).  ;
;  ;
;
2).  ;
;  ;
;
3). 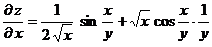 ;
;  ;
;
4).  ;
;  ;
;
5).  ;
;  ;
;
6).  ;
;  ; 7).
; 7).  ;
;  ;
;
8).  ;
;  .
.
3.2. 1).  ; 2).
; 2).  ; 3).
; 3).  ;
;
4).  .
.
3.3. 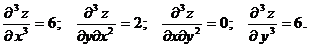
3.4. 

3.6. 1). 

2). 
 кроме точки M (0; 0; 0).
кроме точки M (0; 0; 0).
3.7. 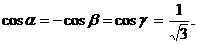
3.8. 1). zmin= 0 в точке (0; 0);
2.) zmin= 0 в точке (1; 0);
3). экстремумов нет;
4). zmin= 0 в точке (0; 0);
5). zmin= -1 в точке (-4; 1);
6). zmax= 1 в точке (0; 0);
7). zmax= 12 в точке (4; 4);
8). zmin=  в точке (-2; 0);
в точке (-2; 0);
9). zmax= a2 в точках (a; a); (-a; -a);
zmin= -a2 в точках (-a; а); (a; -a);
10). zmin= 2 в точке (1; 1);
11). 

12). 
3.9. 

3.10. 

3.11.  3.13. 1).
3.13. 1).  2).
2).  3).
3). 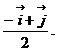
3.14.  3.15. 0.
3.15. 0.
Раздел IV. Неопределенный интеграл
Примеры
Вычислить следующие неопределенные интегралы:
4.1.  ; 4.2.
; 4.2.  ;
;
4.3.  ; 4.4.
; 4.4.  ;
;
4.5.  ; 4.6.
; 4.6.  ;
;
4.7. 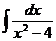 ; 4.8.
; 4.8.  ;
;
4.9.  ; 4.10.
; 4.10.  ;
;
4.11.  ; 4.12.
; 4.12.  ;
;
4.13.  ; 4.14.
; 4.14.  ;
;
4.15.  ; 4.16.
; 4.16. 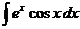 ;
;
4.17.  ; 4.18.
; 4.18.  ;
;
4.19.  ; 4.20.
; 4.20.  ;
;
4.21.  ; 4.22.
; 4.22.  ;
;
4.23.  4.24.
4.24.  ;
;
4.25.  ; 4.26.
; 4.26.  ;
;
4.27.  ; 4.28.
; 4.28.  ;
;
4.29.  ; 4.30.
; 4.30.  ;
;
4.31.  ; 4.32.
; 4.32.  ;
;
4.33.  ; 4.34.
; 4.34.  ;
;
4.35.  ; 4.36.
; 4.36.  ;
;
4.37.  ; 4.38.
; 4.38. 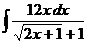 ;
;
4.39.  ; 4.40.
; 4.40.  ;
;
4.41.  ; 4.42.
; 4.42.  ;;
;;
4.43. 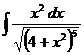 ; 4.44.
; 4.44. 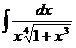 ;
;
4.45.  ; 4.46.
; 4.46. 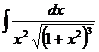 ;
;
4.47. 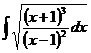 ;
;
Ответы
4.1. x3+c. 4.2.  . 4.3.
. 4.3.  . 4.4.
. 4.4.  .
.
4.5.  . 4.6.
. 4.6.  . 4.7.
. 4.7.  . 4.8.
. 4.8.  .
.
4.9.  . 4.10.
. 4.10.  . 4.11.
. 4.11.  . 4.12. – ln cos x +c.
. 4.12. – ln cos x +c.
4.13. x ln x – x+c. 4.14.  . 4.15.
. 4.15.  .
.
4.16.  . 4.17.
. 4.17.  . 4.18.
. 4.18.  .
.
4.19.  . 4.20.
. 4.20.  . 4.21.
. 4.21.  .
.
4.22.  . 4.23.
. 4.23. 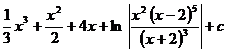 .
.
4.24.  .
.
4.25. 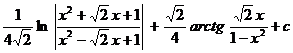 . 4.26.
. 4.26.  .
.
4.27.  . 4.28.
. 4.28.  . 4.29.
. 4.29.  .
.
4.30.  . 4.31.
. 4.31.  .
.


4.34.  . 4.35.
. 4.35.  . 4.36.
. 4.36.  .
.
4.37.  . 4.38.
. 4.38.  .
.
4.39.  . 4.40.
. 4.40.  . 4.41.
. 4.41.  .
.
4.42.  . 4.43.
. 4.43.  .
.
4.44.  . 4.45.
. 4.45.  . 4.46.
. 4.46.  .
.
4.47.  .
.






