Развитие понятия числа, числовые множества

ГЛАВА 1 КОМПЛЕКСНЫЕ ЧИСЛА

В восемнадцатом веке появилось понятие квадратного корня как числа, квадрат которого равен заданному числу. Было показано, что для положительного числа существуют два числа, квадрат которых равен заданному числу. Одно из этих чисел – положительное, другое – отрицательное. Так чему же равен корень квадратный из 4? В школе нас учили, что 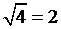, но учебник уточнял, что это арифметический корень. Если спросить очень пожилого человека с хорошей памятью, чему равен , то он скажет  – так раньше учили в школе. Теперь мы говорим, что во втором случае рассматривается алгебраический корень – он для положительного числа принимает 2 значения. В обоих случаях корень квадратный из 0 равен 0, а вот из отрицательных чисел квадратные корни в привычном смысле извлечь нельзя: нет действительного числа , такого что .

Тем не менее развитие математики и ее приложений привело к необходимости использования абстрактных чисел, квадрат которых может быть равен отрицательному числу. В 1545 году итальянский математик Джероламо Кардано предложил ввести нового типа числа, которые мы теперь называем комплексными числами. Важную роль в создании теории комплексных чисел такие выдающиеся математики как французский философ и математик Рене Декарт (1596-1650), действительный член Петербургской Академии наук Пауль Эйлер (1707-1783), немецкий математик Иоганн Гаусс (1777-1855).

Без комплексных чисел никак нельзя было обойтись в развитии науки. Например, в шестнадцатом веке в связи с изучением кубических уравнений оказалось необходимым использовать квадратные корни из отрицательных чисел для получения соответствующих формул. А российский ученый, основоположник современной аэродинамики Николай Егорович Жуковский (1847-1921) использовал функции комплексного переменного для доказательства теоремы о подъемной силе крыла самолета.

ЛЕКЦИЯ 1

Развитие понятия числа, комплексные числа,
геометрический смысл операций над ними

Что мы узнаем на этой лекции

Какие бывают числа? Это натуральные, рациональные, действительные, иррациональное, трансцендентные числа. Какие операции над числами известны нам из школы?

Что такое комплексное число? Какие операции над комплексными числами входят в их определение? Как найти сопряженное комплексное число, сумму, разность, произведение, частное комплексных чисел? В чем заключается геометрический смысл операций сложения, вычитания комплексных чисел, умножения комплексных чисел на действительное число? Можно ли комплексные числа представлять векторами на плоскости?

Как определяется модуль и аргумент комплексного числа? Мы узнаем, в чем заключается геометрический смысл умножения и деления комплексных чисел.

Историческая справка

В VIII в. н.э. было установлено, что для положительного числа 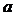 существуют 2 числа – положительное и отрицательное, квадрат которых равен 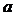. При этом возникло понятие квадратного корня. Арифметический квадратный корень из 4 равен 2, а алгебраический квадратный корень из 4 принимает два значения: 2 и -2. Из отрицательных чисел квадратные корни извлечь нельзя: нет числа , такого  что .

В XVI в. в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. Только таким образом можно было получить формулу для решения кубических уравнений.

Чтобы объяснить получившийся парадокс, итальянский алгебраист Дж. Кардано в 1545 году предложил ввести числа новой природы. Он показал, что система уравнений  не имеющая решений в множестве действительных чисел, имеет решения вида , . Нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать, что . Кардано называл такие величины «чисто отрицательными» и даже «софистически отрицательными», считал их бесполезными и стремился не применять их. В самом деле, с помощью таких чисел нельзя выразить ни результат измерения какой-нибудь величины, ни изменение этой величины. Но уже в 1572 г. вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены первые правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней. Название «мнимые числа» ввел в 1637 г. французский математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII века – Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа («мнимой» единицы); этот символ вошел во всеобщее употребление благодаря К. Гауссу (1831).

Развитие понятия числа, числовые множества

Рассмотрим множество  натуральных чисел, т. е. числа . Для них операции сложения и умножения дают в результате снова натуральные числа. Нам знакомы свойства этих операций: , , , , , , . Также для этих чисел можно ввести операцию возведения в натуральную степень , при этом справедливы соотношения 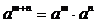, , . Попытка ввести обратные операции приводит нас к необходимости расширения понятия числа. Для множества  целых чисел, т.е. для чисел  доступно вычитание чисел, обратное их сложению. А попытка ввести операцию деления чисел, обратную к операции умножения, приводит к дальнейшему развитию понятия числа, а именно, к введению рациональных чисел.

Рациональными называются числа вида 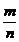, где  является целым числом (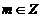), а  – натуральное число (). Множество рациональных чисел принято обозначать буквой . Рациональные числа содержат в себе целые числа, их можно понимать как корни уравнения .

Дальнейшее развитие понятия числа можно воспринимать как решение все более сложных уравнений. Например, в школьном учебнике доказывается, что уравнение  не имеет решение среди рациональных чисел. Конечные и бесконечные десятичные дроби (множество всех точек числовой оси) образуют множество действительных чисел 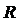. Действительные числа, не являющиеся рациональными, называются иррациональными числами. Как мы видим, иррациональные числа существуют, например, это любой корень уравнения .

Отметим еще одно понятие – трансцендентное число. Это иррациональные числа, которые не являются корнями алгебраического уравнения с целыми коэффициентами. Таких чисел подавляющее большинство на числовой оси. Поэтому, как правило, мировые константы являются трансцендентными числами.