Требуемый состав практической работы.

В результате выполнения всех разделов работы в отчете по ней должны быть представлены:

- гистограмма распределения показателя качества;

- оценка соответствия закона распределения заданного статистического ансамбля нормальному закону распределения по критериям хи-квадрат и критерию Колмогорова;

- значение установленного поля допуска и минимального объема испытаний;

- оперативная характеристика контроля

 

Исходные данные (статистический ансамбль)                      Таблица 2.1

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
98	51	30	21	90	60	110	85	120	235	158	42	30	14	91	97	23	50	41	110
106	64	35	26	72	24	151	101	147	241	168	50	30	16	73	105	28	55	46	92
84	61	25	33	89	55	157	104	151	220	175	72	20	15	90	83	35	45	53	109
119	59	32	34	66	42	112	86	175	230	180	66	39	16	67	118	36	52	54	86
76	36	33	27	90	40	139	98	155	246	190	56	33	17	91	75	29	53	47	110
81	36	28	34	86	31	127	105	141	255	188	40	28	16	87	80	36	48	54	106
96	42	27	34	66	40	159	87	151	252	179	51	65	18	67	95	36	47	53	86
101	37	21	97	62	47	139	102	162	254	174	74	65	18	63	100	29	41	47	82
99	52	26	32	76	51	141	96	159	246	167	62	30	20	77	58	54	46	52	96
87	54	28	25	80	55	146	104	132	271	156	67	47	21	81	86	20	48	45	100
88	65	22	22	82	34	158	102	222	154	60	60	27	20	83	87	42	42	42	102
71	53	26	20	71	33	111	96	130	244	165	65	33	20	72	70	20	46	40	91
88	48	16	22	71	43	132	103	129	236	173	68	30	20	72	87	22	26	42	91
76	51	28	23	89	28	141	95	169	245	178	44	31	20	90	75	25	48	43	109
92	47	18	29	60	41	140	100	152	237	186	76	31	23	61	91	29	38	49	80
91	50	26	29	69	21	141	100	131	224	184	51	36	24	63	90	28	46	49	89
75	37	29	22	65	59	110	115	147	232	176	48	31	22	66	74	24	49	42	85
86	63	26	20	79	22	145	113	131	247	164	46	56	24	80	85	23	46	40	99
93	49	25	20	76	41	146	96	171	249	152	80	36	22	77	92	25	45	40	96
74	64	27	23	72	38	139	98	180	254	150	65	40	22	73	73	23	47	43	92
115	56	19	28	83	32	131	88	176	248	163	53	10	22	84	114	28	39	48	103
96	50	28	16	65	44	157	90	154	256	172	59	60	24	66	95	20	48	56	85
112	51	23	26	83	48	158	91	167	234	177	48	45	22	84	114	24	43	46	103
99	51	21	28	72	52	113	96	158	224	182	68	49	22	73	98	26	41	48	92
70	65	27	36	82	56	138	94	161	238	160	69	44	23	83	69	30	47	56	102
96	36	17	29	75	35	139	92	156	237	169	40	43	25	76	95	30	37	49	95
113	43	19	20	71	38	139	93	178	241	160	53	39	22	72	112	31	29	40	91
79	48	20	37	72	31	129	98	184	244	170	58	51	27	94	79	29	40	57	92
80	56	18	27	93	25	138	95	250	271	163	57	44	22	83	95	24	38	47	113
96	51	19	21	82	39	139	99	159	248	162	62	50	23	87	114	30	39	41	102
115	61	29	29	86	49	139	97	162	257	176	66	52	24	84	97	18	49	49	106
96	59	33	10	83	52	142	100	147	243	162	61	42	23	65	97	31	53	30	103
98	54	20	29	64	27	132	98	171	239	178	59	4	20	72	97	17	40	49	84
98	55	30	15	76	42	141	104	149	244	166	78	39	19	88	100	28	50	35	91
101	61	24	28	84	37	140	99	162	241	158	42	51	16	76	105	15	44	48	107
106	56	23	13	75	39	141	101	151	257	173	64	47	22	89	91	21	43	33	95
92	56	32	28	88	45	137	109	155	233	178	60	43	24	88	90	34	62	48	108
91	51	24	37	87	49	134	106	147	231	165	61	45	25	69	101	22	44	57	107
102	49	16	22	68	53	140	104	124	241	171	59	41	15	88	88	23	36	42	88
89	61	17	23	87	32	140	96	156	228	173	46	39	16	57	97	19	37	43	107
98	55	25	24	56	31	141	97	161	243	170	74	52	25	70	109	28	45	44	76
110	58	30	23	69	34	149	99	154	240	162	59	55	26	83	95	24	50	43	89
96	49	18	22	82	37	142	96	159	236	180	56	45	24	78	89	31	38	42	102
90	56	18	21	77	37	150	100	151	257	171	69	47	22	72	85	19	38	41	97
86	52	17	21	71	34	156	110	175	232	171	63	38	28	80	95	24	27	41	91
96	51	26	28	79	54	139	112	131	243	173	79	44	23	83	101	28	46	48	99

2.1. Содержание разделов и методические

указания по их выполнению.

1. Построение гистограммы распределения показателя качества.

Для построения гистограммы заданную в качестве исходных данных выборку показателей качества x_i(статистический ряд) разбивают на r(от 10 до 16) интервалов. Величина интервала определяется по формуле Стэрджеса

 

(2.1)

где h –значение величины интервала параметра качества;

x_max, x_min – соответственно максимальное и минимальное значения показателя качества, определяемое по данным табл. 1;

n – число значений показателя качества.

Для полученного значения величины интервала определяется число значений n_i^э показателей качества в каждом из r интервалов, а результаты заносятся в табл. 2.2

Таблица. 2.2

Ранжирование выборки по интервалам

Xi	xmin+h	xmin+2h	….	….	….	xmin+ i*h	….	….	….	xmin+(r-1)*h	xmin+ r*h
niэ	n1э	n2э				niэ				nr-1э	nrэ

Значение 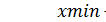может быть ≥ x_max.

В первый интервал (от x_minдо x_min+h) заносится число значений параметров качества, соответствующих границам первого интервала, во второй интервал (отx_min+hдоx_min+2h) - соответственно число значений, соответствующих границам этого интервала и т.д. Параметр качества, значение которого равно границе интервала, считается принадлежащим интервалу, находящемуся ближе к среднему интервалу.

По определенному (табл.2.2) ранжированию выборки строится гистограмма распределения показателей качества (рис.2.1).

 

 

n

 

 

                                                                  x_i

Рис.2.1. Гистограмма распределения характеристик неразрушающего контроля .

 

 

2. Проверка предполагаемого закона распределениязаданного статистического ряда показателя качества.

Проверка согласия предполакаемого нормального закона распределения с законом распределения заданного статистического ряда выполняется по критерию хи-квадрат. Расчет для проверки согласия производится по формулам (2)-(8).

 

Определяется объем выборки

r

n= ∑ n_i^э(2.2)

i=1

Определяется среднее значение выборки

r       r

x _ср = ∑ x_{i ср} n_i^э / ∑ n_i^э(2.3)

                                i=1   i=1

Определяется значение дисперсии           

r

s² = ∑ Δx_i ² _* n_i^э / (n-1)(2.4)

i=1

Здесь

(2.5),

Где: x_{i ср} - значение середины каждого принятого интервала,

r– принятоечислоинтервалов.

Значения величины плотности вероятности нормального закона распределения φ_ί в зависимости от значения аргумента определяется по табл. 2 3. Для повышения точности выполняемых расчетов промежуточные значения следует определять линейной интерполяцией их табличных величин.

                                                                                         Таблица 2.3

Плотность вероятности нормального распределения.

Δxi/s	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	1,0	1,1
φί	0,3989	0,3970	0,3910	0,3814	0,3683	0,3581	0,3332	0,3123	0,2897	0,2420	0,2179
Δxi /s	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9	2,0	2,1	2,2
φί	0,1942	0,1714	0,1497	0,1295	0,1109	0,0940	0,0790	0,0656	0,0540	0,0440	0,0355
Δxi /s	2,3	2,4	2,5	2,6	2,7	2,8	2,9	3,0	3,2	3,5	4,0
φί	0.0283	0,0224	0,0175	0,0140	0,0105	0,0079	0,0059	0,0044	0,0027	0,0009	0,0001

 

Вычисляются значения 

(2.6)

теоретического объема выборки

 

n_i^т= f_ί*n_ί*h(3.7)

 

Определяются значения коэффициентов

 

β_ί =(n_i^т - n_i^э)² /n_i^т(2.8)

Результаты расчетов проверки согласия по критерию хи-квадрат представляются в форме табл.2.4.

                                                                                               Таблица 2.4

xi ср	niэ	xi ср*niэ	Δxi	Δxi 2	Δxi 2* niэ	Δxi /s	φί	fί	niт	niт - niэ	βί
...................................

 

 

При вычислении оценки согласия по критерию хи-квадрат крайние интервалы, содержащие менее пяти значений показателя качества, необходимо объединять.

Затем вычисляется значение

     r

y=∑β_ί / k(2.9)

i=1

Здесь k– число степеней свободы, определяемое из соотношения

 

(2.10)

Где c– число параметров закона распределения. Для нормального закона распределения c =2.

Полученное значение yсравнивается с табличным значением (см. табл.2.5) распределения хи-квадрат при небольшом (порядка 0,1) значении доверительной вероятности

 

Таблица 2.5.

                           Значение yраспределения хи-квадрат.

K	α.
	0,010	0,025	0,050	0,100	0,200	0,300
10	0,256	0,325	0,394	0,487	0,618	0,727
11	0,278	0,347	0,416	0,507	0,635	0,741
12	0,298	0,367	0,436	0,525	0,651	0,753
13	0,316	0,385	0,453	0,542	0,664	0,764
14	0,333	0,402	0,469	0,556	0,676	0,773
15	0,349	0,418	0,484	0,570	0,687	0,781
16	0,363	0,432	0,498	0,582	0,697	0,789

 

В тех случаях, когда табличное значение величиныyбольше вычисленного по формуле (2.9), согласие экспериментально полученных значений заданного статистического ряда с предполагаемым нормальным законом распределения может считаться хорошим. По результатам проверки по критерию хи-квадрат делается вывод о характере согласия (хорошее или плохое).

Производится проверка согласия предполагаемого закона распределения по критерию Колмогорова. Вычисления выполняются по форме табл. 2.6, в которую заносятся конечные значения интервалов x_iк и количество значений параметра в каждом интервале n_ί.Затем определяется экспериментальная частость появления параметра качествав каждом интервале n_ί /n,после чеговычисляется накопленная экспериментальная частость

r

F_эj =∑n_ί / n(2.11)

i=1

Определяется накопленная теоретическая частость как функця от по табл. 2.6

F_тj=f(x_iк- x _ср) / s(2.12)

 

 

                                                                             Таблица 2.6

Значение функции F_т нормального распределения

(xiк- xср) / s	0,00	0,05	0,01	0,20	0,30	0,40	0,50	0,60	0,70	0,80
Fт	0,5000	0,5199	0,5398	0,5793	0,6179	0,6554	0,6915	0,7257	0,7580	0,7881
(xiк- xср) / s	0,90	1,00	1,10	1,20	1,30	1,40	1,50	1,60	1,70	1,80
Fт	0,8159	0.8413	0,8631	0,8849	0,9020	0,9192	0,9322	0,9452	0,9555	0,9641
(xiк- xср) / s	1,90	2,00	2,10	2,20	2,40	2,60	2,80	3,00	3,50	4,00
Fт	0,9706	0,9772	0,9816	0,9861	0,9918	0,9953	0,9974	0,9986	0,9998	0,9999

 

Затем определяется абсолютное значение разницы накопленной и экспериментальной частости

(2.13)

Расчет выполняется по форме табл. 2.7.

 

Таблица 2.7

Проверка по критерию Колмогорова

xiк	nί	nί / n	Fэj	(xiк- xср) / s	Fтj	ΔF
.............................

 

Из всех полученных значений выбирается максимальное значение исопоставляется с табличным (табл.8) или вычисленном по формулам (2.14 или 2.15).

                                                                                         Таблица 2. 8

Значения критерия Колмогорова ΔF

n	α
	0,8	0,9
20	0,232	0,265
50	0,148	0,170
80	0,118	0,135
100	0,106	0,121

 

Для значений n> 100 при и при

Согласие заданного статистического ряда с теоретическим законом нормального распределения считается плохим, если вычисленное эмпирическое значение критерия Колмогорова больше теоретического, т.е. .При определении согласия по критерию Колмогорова вероятность α следует брать не менее 0,8. При меньших значениях α заранее планируется малая вероятность события, что свидетельствует о плохом согласии с предполагаемым нормальным законом распределения.

По выполненным расчетам строятся гистограмма, теоретическая и экспериментальная плотности распределения (рис.2.2), интегральные функции теоретическая и экспериментальная по данным табл. 6 (рис.2.3).Экспериментальные значения наносятся в виде отдельных точек. На графиках (см. рис.2.2 и рис.2.3) необходимо указать значения x _ср,s,ΔF_max.

 

                  

Рис.2.2. Гистограмма, теоретическая и экспериментальная плотности

нормального распределения       

                                         F_т

                                     x _ср                                   x_i

 

Рис. 2.3. Интегральные функции (теоретическая и экспериментальная).

3. Установление поля допуска.

Величина поля допуска обычно устанавливается по полученным значениям среднего и среднеквадратического параметра качества при выбранной двухсторонней вероятности α = 0,90; или α =0,95; или α= 0,99. Рекомендуется принимать значение величины поля допуска в пределах ±2 s. Установленное таким образом поле допуска следует нанести на ранее построенные графики (см. рис.2.2).

4. Расчет числа необходимых проверок при контроле качества.

Определение числа необходимых проверок при контроле качества сводится к планированию величины малой выборки n_м для оценки среднего значения. Для этого следует задаться значением доверительной вероятности α = 0,90 или α =0,95 и предельной абсолютной ошибкой среднего ε. Величина абсолютной ошибки среднего может быть определена в долях от среднеквадратического – (0,3…1,0) s. Длявыбранного значения доверительной вероятности и абсолютной ошибки среднего определяется величина s / ε, а по ней - величина малой выборкиn_м в функции от отношения s / ε по табл. 2.9.

 

                                                                                         Таблица 2.9

Значение объема выборки n_м в функции от соотношения s / ε

nм	α		nм	α		nм	α
	0,90	0,95		0,90	0,95		0,90	0,95
2	1,167	1,390	7	0,620	0,739	12	0,475	0,566
3	0,950	1,130	8	0,581	0,692	13	0,455	0,543
4	0,822	0,980	9	0,548	0,653	14	0,440	0,524
5	0,734	0,874	10	0,520	0,620	15	0,425	0,506
6	0,671	0,800	11	0,495	0,590	20	0,365	0,438

 

Значение предельной абсолютной ошибки среднего ε наносится на график плотности вероятности (см. рис.2.2). Если значение малой выборки размером n_м попадает внутрь этих границ, то среднее значение параметра, для оценки которого сделана малая выборка, совпадает со значением среднего x _ср , определенного в п.4.1, с вероятностью α. Затем строится оперативная характеристика контроля, выражающая зависимость вероятности приемки всей партии изделий от значения      выборочного среднего L (x_ср).

 

(2.15)

 

Значение c₁ (приемочное число) принимается по нижней границе среднего, определяемой по формуле

  (2.16)

При определении значения нижней границы x_н величину t / √nдля заданногов табл. 2.1 количества выполненных измерений принимаем равным 0,24. Значение F₀ определяется из табл.2.7 для выбранной вероятностиα (0,8 или 0,9).

Для построения оперативной характеристики значение x _ср  задается через 0,05 влево и вправо от c₁. По трем полученным значениям P (x _ср) строится опративная характеристика контроля (рис. 2.4).

Оценка партии по величине x _ср выполняется для двух уровней: x_o(браковочный уровень)иx_m(приемочный уровень), причемx_o>x_m. Полагая риск поставщика α₁ равным 0,05, а риск заказчика β =0,20, находятся величины x_oиx_mиз выражений

 

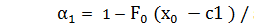(2.17)

 

(2.18)

Найденные величиныx_oиx_mнаносятся на оперативную характеристику, определяется зона хорошего качества (0 - x_m), браковочного качества (x_o>x_m) и зона неопределенности (x_m -x_o).

 

                                            x_m  x_o                                                 x _ср

Рис.2.4. Оперативная характеристика контроля

 

3. ΙΙРАЗРАБОТКА КОНТРОЛЬНОЙ КАРТЫ.

ОЦЕНКИ СТАБИЛЬНОСТИ ТЕХНОЛОГИЧЕСКИХ

ПРОЦЕССОВ.

 

 Общие сведения и цель практической работы.

Контрольная карта применяется в тех случаях, когда требуется установить, сколько колебаний в технологическом процессе вызываются случайными причинами и сколько обязаны чрезвычайным обстоятельствам или отдельным действиям, чтобы определить поддается ли процесс статистическому регулированию.

Контрольная карта представляет собой графическое представление временного ряда со статистически определенной верхней и нижней границей (верхний контрольный предел и нижний контрольный предел), нанесенной на график по обе стороны от средней линии, характеризующей стабильность изучаемого технологического процесса.

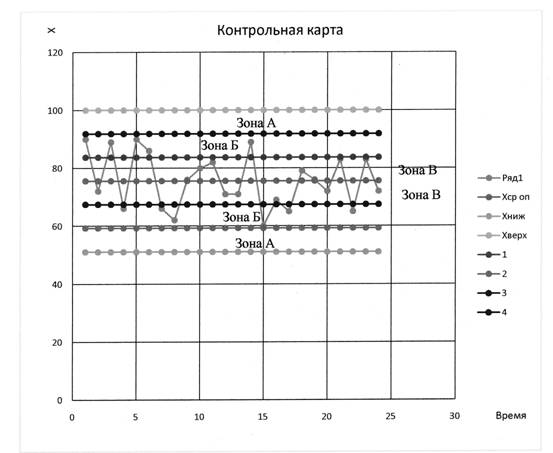
Рис.3.1.Контрольная карта

 

Эти пределы вычисляются по особым формулам с использованием отдельных замеров. При этом принимается во внимание как идет весь процесс после нанесения границы процесса на схему, чтобы далее определить, попадают ли точки между линиями пределов или они выходят за них образуют неестественные выбросы. Если это происходит, то считается, что процесс вышел из-под контроля. Отклонение точек внутри пределов происходит из-за изменений, присущих самому процессу (конструкции выбора машин и т. п.). Повлиять на эти колебания можно только изменением системы.

Это наиболее сложный из статистических методов контроля качества. Формулы к нему из-за сложности даются без выводов, ими нужно только научиться пользоваться.

Верхний и нижний контрольные пределы определяются статистическими методами и не являются пределами (допусками) технических характеристик, назначаемых требованиями стандартов. Данные должны быть взяты точно в той последовательности, как они собраны, иначе они теряют смысл. В процессе сбора данных не следует вносить изменение (корректировать) в процесс; он должен идти естественным образом.

Контрольная карта может указать на наличие потенциальных проблем до того, как пойдет дефектная продукция. Считается, что процесс вышел из-под контроля, если одни и больше точек вышли за пределы контроля..

При разделении контрольной карты на зоны корректировка процесса необходима при условии, что:

- 2 точки из 3-х находятся на одну сторону от центральной линии в зоне А или дальше;

- 4 точки из 5-ти расположены по одну сторону от центральной линии в зоне Б или далее;

- 9 точек находятся по одну сторону от центральной линии;

- 6 последовательных точек возрастают или уменьшаются;

- 14 точек в ряду колеблются вверх-вниз;

- 15 точек в ряду находятся в зоне В (ниже или выше центральной линии).

Имеется 2 типа контрольных карт: для контроля по качественному признаку (годен-негоден) и для контроля по количественному признаку.

Для контроля по качественному признаку используются 4 вида контрольных карт:

U-карта (число дефектов на единицу продукции);

С-карта (число дефектов в выборке);

Р-карта (доля дефектных изделий в выборке);

ňр- карта (число дефектных изделий в выборке).

Для U и Р объем выборки является переменным; С, ňр – постоянным.

Для чего применяются контрольные карты:

Цель: выявление неуправляемого процесса; контроль за управляемым процессом, оценка возможностей процесса.

       Обычно изучается один из параметров процесса (переменная величина):

- известная важная или важнейшая характеристика;

- предположительная ненадежная характеристика;

- характеристика процесса, по которой нужно получить информацию о возможности процесса;

- эксплуатационная характеристика, имеющая значение при маркетинге.

       Контрольные карты следует использовать разумно (стоят денег): тщательно выбирать характеристики, прекращать работу с картами при достижении поставленной цели, продолжать вести карты, если процессы и технические требования находятся в противоречии.

       Нужно иметь в виду, что статистически регулируемый процесс может давать 100 % брака, а неуправляемый 100 % - годную продукцию.

Контрольные карты позволяют проводить анализ возможностей процесса – присущей процессу способности функционировать должным образом, т. е. удовлетворять техническим требованиям.

 Исходные данные для выполнения работы.

Практическая работа выполняется на основании статистического ансамбля по одной из характеристик качества конструктивных материалов для судостроения (модуль упругости, предел прочности, плотность, толщина конструкции, результаты дефектоскопии готовых конструкций и др.), полученных по результатам неразрушающего контроля.

Исходные данные для выполнения практической работы выдаются студенту по данным реальных испытаний, проведенных в лабораториях судостроительных предприятий и переданных на кафедру технологии судостроения. Эти данные для двадцати вариантов выполнения работы представлены в табл. 3.1.

Таблица 3.1

Исходные данные (статистический ансамбль)

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
98	51	30	21	90	60	110	85	120	235	158	42	30	14	91	97	23	50	41	110
106	64	35	26	72	24	151	101	147	241	168	50	30	16	73	105	28	55	46	92
84	61	25	33	89	55	157	104	151	220	175	72	20	15	90	83	35	45	53	109
119	59	32	34	66	42	112	86	175	230	180	66	39	16	67	118	36	52	54	86
76	36	33	27	90	40	139	98	155	246	190	56	33	17	91	75	29	53	47	110
81	36	28	34	86	31	127	105	141	255	188	40	28	16	87	80	36	48	54	106
96	42	27	34	66	40	159	87	151	252	179	51	65	18	67	95	36	47	53	86
101	37	21	97	62	47	139	102	162	254	174	74	65	18	63	100	29	41	47	82
99	52	26	32	76	51	141	96	159	246	167	62	30	20	77	58	54	46	52	96
87	54	28	25	80	55	146	104	132	271	156	67	47	21	81	86	20	48	45	100
88	65	22	22	82	34	158	102	222	154	60	60	27	20	83	87	42	42	42	102
71	53	26	20	71	33	111	96	130	244	165	65	33	20	72	70	20	46	40	91
88	48	16	22	71	43	132	103	129	236	173	68	30	20	72	87	22	26	42	91
76	51	28	23	89	28	141	95	169	245	178	44	31	20	90	75	25	48	43	109
92	47	18	29	60	41	140	100	152	237	186	76	31	23	61	91	29	38	49	80
91	50	26	29	69	21	141	100	131	224	184	51	36	24	63	90	28	46	49	89
75	37	29	22	65	59	110	115	147	232	176	48	31	22	66	74	24	49	42	85
86	63	26	20	79	22	145	113	131	247	164	46	56	24	80	85	23	46	40	99
93	49	25	20	76	41	146	96	171	249	152	80	36	22	77	92	25	45	40	96

Примечание: в первой строке таблицы указан вариант выполнения работы.