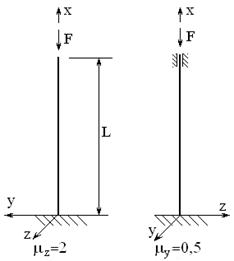
Для заданной стойки подобрать сечение, указанной формы, определить величину критической силы, вычислить значение коэффициента запаса устойчивости. Схема крепления стойки показана на рис. 2.15, форма поперечного сечения – на рис. 2.16.
| 
|
| Рис. 2.15 | Рис. 2.16 |
Дано: длина стойки L =2,5 м, сжимающая сила F =330 кН =33000 кг, допускаемое напряжение материала [σ]=1600 кг/см 2, предел текучести σт=2000 кг/см 2, модуль упругости материала Е =2·106 кг/см 2.
Решение
1. Выбор положения стержня относительно опор крепления.
Из рисунка 2.16 видно, что момент инерции сечения стойки относительно оси y значительно меньше, чем относительно оси z. Следовательно, гибкость относительно оси y большая (относительно этой оси стойка неустойчива). Уменьшить гибкость относительно оси y можно путем выбора расположения стойки, как показано на рисунке 2.16. В данном случае коэффициент крепления относительно данной оси меньше, чем относительно оси z.
Дальнейший расчет по определению сечения стойки производится методом последовательных приближений.
2. Первое приближение.
Выбираем коэффициент снижения допускаемого напряжения φ1=0,5. Из условия устойчивости следует, что
 см 2.
см 2.
Получено значение площади поперечного сечения стойки, а для одного двутавра  см 2. По таблице сортамента находим двутавр № 18, для которого выписываем следующие характеристики: размеры двутавра h =18 см, b =9 см, площадь поперечного сечения А 1=23 см 2, моменты инерции Jz' =1290 см 4, Jy' =82,6 см 4.
см 2. По таблице сортамента находим двутавр № 18, для которого выписываем следующие характеристики: размеры двутавра h =18 см, b =9 см, площадь поперечного сечения А 1=23 см 2, моменты инерции Jz' =1290 см 4, Jy' =82,6 см 4.
Определим характеристики сечения стойки:
Ас =46,8 см2, 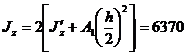 см 2,
см 2, 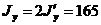 см2.
см2.
Находим радиусы инерции:
 см,
см, 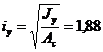 см.
см.
Определяем гибкость:

По наибольшей гибкости в таблице коэффициентов путем интерполяции находим φ=0,83. Оцениваем погрешность φ первого приближения
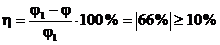 .
.
Определяем нормальное напряжение, возникающее в стойке, если ее сечение – два двутавра № 18.
 кг/см 2 <
кг/см 2 <  кг/см 2.
кг/см 2.
Полученное значение напряжения значительно ниже допускаемого, поэтому можно принять двутавр меньшего размера.
3. Второе приближение.
Параметры двутавра № 16: h =16 см, b =8,1 см, A 1=20,2 см 2, Jz' =873 см 4, Jy '=58,6 см 4.
Далее повторяем вычисления, выполненные при первом приближении: Ас =40,4 см 2, Jz =4330 см 4, Jy =117 см 4, iz =10,4 см, iy =1,7 см, λ z =48,1, λ y =73,5.
По таблице для λmax находим φ=0,78.
Определяем нормальное напряжение, возникающее в стойке, если ее сечение – два двутавра № 16.
 кг/см 2 <
кг/см 2 <  .
.
Так как полученное напряжение меньше допустимого возьмем двутавр меньшего размера.
4. Третье приближение.
Параметры двутавра № 14: h =14 см, b =7,3 см, A 1=17,4 см 2, Jz' =572 см 4, Jy' =41,9 см 4.
Далее повторяем вычисления, выполненные при первом и втором приближениях: Ас =34,8 см 2, Jz =2850 см 4, Jy =83,8 см 4, iz =9,04 см, iy =1,55 см, λz=55,3, λy=80,6.
По таблице для λmax находим φ=0,75.
Определяем нормальное напряжение, возникающее в стойке, если ее сечение – два двутавра № 14.
 кг/см 2 <
кг/см 2 <  .
.
Полученный результат позволяет в очередной раз уменьшить номер двутавра.
5. Четвертое приближение.
Параметры двутавра № 12: h =12 см, b =6,4 см, A 1=14,7 см 2, Jz' =350 см 4, Jy' =27,9 см 4.
Далее повторяем вычисления, выполненные при первом и втором приближениях: Ас =29,4 см 2, Jz =1760 см 4, Jy =55,8 см 4, iz =7,74 см, iy =1,38 см, λz=64,6, λy=90,6.
По таблице для λmax находим φ=0,69.
Определяем нормальное напряжение, возникающее в стойке, если ее сечение – два двутавра № 12.
 кг/см 2 >
кг/см 2 >  .
.
Таким образом, останавливаемся на номере двутавра № 14 для изготовления стойки. Условие устойчивости стойки при этом выполняется.
6. Определим величину критической силы и коэффициент запаса на устойчивость.
Так как гибкость стойки меньше предельной для стали  , то критические силу и напряжение определяют по эмпирическим формулам.
, то критические силу и напряжение определяют по эмпирическим формулам.
По формуле Ф.С. Ясинского
 ,
,
где а =310 мП =3100 кг/см 2, b =1,14 мП =11,4 кг/см 2 – коэффициенты для стали Ст. 3.
В этом случае  кг/см 2.
кг/см 2.
Критическая сила  кг = 7,2 кН.
кг = 7,2 кН.
Коэффициент запаса на устойчивость
 .
.
| Приложение А Таблица измерения основных величин | 
|


Приложение Б




