Решение статически неопределимых задач

Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум другим упругим стержням (рис. 2.5). Определить максимальную величину нагрузки F, при которой система работает в упругой стадии, и сравнить с предельной грузоподъемностью системы F _пред (несущей способности). На схеме размеры показаны в метрах.

Исходные данные. Площади поперечного сечения стержней одинаковы А =15·10^–4 м ², допускаемое напряжение материала [σ]=220·10⁶ Па, предел текучести σ_т=225·10⁶ Па.

Решение

1. Определим для заданной стержневой системы максимальную величину нагрузки F при работе в области упругих деформаций.

Определим значение угла α: tg α=2, следовательно α=63,4^о, sin α=0,894; cos α=0,448.

 

Рис. 2.5

Составим уравнение статики

, или

                            .                            (а)

Для составления уравнения совместности деформаций составим схему (рис. 2.6). Обозначим ВВ '=δ_В, СС '=δ_С. Для данной схемы перемещения точек В и С при деформации

δ_В=δ_С                                      (б).

Деформация стержня 1 равна Δ L ₁=δ_В. Деформация стержня 2 равна Δ L ₂=δ_Csin α=0,894δ_C. Отсюда δ_С=1,12Δ L ₂. С учетом выражения (б) получим   и раскроем

                           .                                (в)

Имеем два уравнения (а) и (в) с двумя неизвестными N ₁ и N ₂. Длина второго стержня   м. Из уравнения (в) имеем . Этот результат подставим (а) и получим

В наиболее опасном состоянии находится стержень 1. Величину нагрузки определим из условия максимального напряжения первого стержня

Па.

Отсюда кН.

Допускаемая величина нагрузки F при расчете системы по упругому состоянию равна 377 кН.

 

2. Рассчитаем величину силы F по несущей способности.

В этом случае используем уравнение статики (а), когда оба стержня нагружены внутренними усилиями, соответствующими пределу текучести σ_т=225·10⁶ Па,   кН. Тогда . Отсюда кН.

То есть, допускаемая сила F при расчете по несущей способности равна 427 кН.

 

Рис. 2.6

 

РАСЧЕТНАЯ РАБОТА № 3.

РАСЧЕТ БАЛКИ НА ПРОЧНОСТЬ

Для прямой балки, используя метод сечений, построить эпюры поперечных сил Q_y, и изгибающих моментов M_z. Выполнить расчёт балки на прочность, подобрав поперечное сечение балки в виде круга, прямоугольника с соотношением сторон h / b =2 и двутавра. Выполнить сравнительный весовой анализ балок с данными сечениями. Построить эпюры распределения нормальных «σ» и касательных «τ» напряжений в опасном сечении балки. Выполнить проверку принятого сечения по главным напряжениям, используя третью теорию прочности. Материал балки сталь Ст3. [s]=160 мПа; [t]=100 мПа.

Схема нагружения балки приведена на рисунке 3.1. Исходные данные: F ₁=3 кН, F ₂=1,5 кН, М ₀=5,1 кНм, q =2 кН/м, удельный вес материала g=7850 кг/м³.

Решение

1. Определим опорные реакции.

С этой целью составляются два уравнения равновесия:

Получим решения: R_A =5,7 кН, R_B =4,8 кН.

 

2. Определим внутренние усилия.

Для произвольного сечения внутренние усилия определяются следующим образом.

; .

Балка разбивается на участки, границами которых являются сосредоточенные силы и моменты, начало и конец распределенной нагрузки.

Участок 1.

 На данном участке поперечная сила постоянна, а момент пропорционален координате x. При x =0 M =0, при x =2 м M =–6 кНм.

Участок 2.

 Числовые значения внутренних усилий приведены на соответсвующих графиках (рисунок 2.7).

Участок 3.

Участок 4.

На данном этапе эпюра изгибающего момента изменяется скачком в месте приложения внешнего момента.

Участок 5.

В выражении изгибающего момента координата x имеет вторую степень, что указывает на параболический профиль кривой. В этом случае необходимо определить экстремум функции изгибающего момента, который должен располагаться под значением Q =0. Определим координату, определяющую положение экстремального значения изгибающего момента,  Далее подставим в уравнение для изгибающего момента м. Получим кНм. Необходимо помнить, что положительные значения изгибающего момента откладваются вниз.

 

3. Рассчитаем размеры сечений.

Определим требуемый осевой момент сопротивления поперечного сечения балки.

37,5·10^–6 м ³.

А. Круглое сечение.

. Следовательно   м.

Погонный вес такой балки   кг.

Б. Прямоугольное сечение с соотношением сторон h =2 b.

Следовательно   м, h=0,0766 м. Погонный вес такой балки   кг.

 

 

Рис. 2.7

 

В. Двутавровое сечение.

Для W =37,5·10^–6 м³ выбираем из сортамента прокатных профилей двутавр № 10, для которого W =39,7·10^–6 м³,      А =12·10^–4 м², момент инерции J_z =198·10^–8 м⁴, статический момент сечения S_z =23·10^–6 м³, d =0,0045 м. Погонный вес такой балки   кг.

Определим перерасход материала на изготовление балки круглого и прямоугольного сечений относительно балки двутаврового сечения. Имеем в виду, что вес пропорционален поперечному сечению балки. Поэтому

, .

Таким образом, наиболее рациональной формой поперечного сечения стальной балки, с точки зрения расхода материала, является двутавровое сечение.

 

4. Проверим прочность двутавра:

  мПа < [σ]=160 мПа;

  мПа < [τ]=100 мПа.

Прочность балки по нормальным и касательным напряжениям обеспечена.

Осуществим проверку сложного сопротивления балки по четвертой теории прочности. Выбираем сечение А, для которого М_А =6 кН, Q_A =3 кН:

 

Расчетное напряжение по четвертой теории прочности

  мПа < [σ]=160 мПа.

Прочность балки обеспечена.

 

5. Построим эпюры нормальных и касательных напряжений в опасном сечении балки.

Для построении эпюры нормальных напряжений применим формулу Навье . Так как напряжение пропорционально координате y (функция линейна), поэтому достаточно рассчитать напряжения в двух (максимум в трех точках). .  (рис. 2.8, а).

 

Рис. 2.8

 

Для построения эпюры касательных напряжений применим формулу Журавского , где 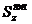 – статический момент отсеченной части поперечного сечения, δ _i толщина i –го слоя сечения.

В точке 1 статический момент отсеченной части сечения равен нулю, следовательно и касательные напряжения равны нулю.

В точке 2, расположенной непосредственно над линией, проходящей через нижнюю грань верхней полки двутавра

  Па.

В точке 3, расположенной непосредственно под точкой 2

  Па.

Наибольшие касательные напряжения возникают на уровне нейтральной оси.

  Па (рис. 2.8, б).

 

РАСЧЕТНАЯ РАБОТА № 4.

РАСЧЕТ БАЛКИ НА ЖЕСТКОСТЬ

Для стальной балки, подобранной по условиям прочности в предыдущей задаче (РР № 3), построить изогнутую ось, используя метод начальных параметров.

Исходные данные: F ₁=3 кН, F ₂=1,5 кН, М ₀=5,1 кНм, q =2 кН/м, R_A =5,7 кН, R_B =4,8 кН, Е =2,1·10¹¹ Па, J_z =198·10^–8 м ⁴.

Решение

Для проверки сечения балки по условию жесткости примем

  см.

Основные уравнения метода начальных параметров:

;

+

1. Определим начальные параметры. Начальные параметры находятся из условия крепления балки. Составим уравнения прогибов для опор A и B.

При x =2                (а)

При x =9

(б)

Совместное решение уравнений (а) и (б) дает

  кНм³,   кНм².

 

2. Определим угол поворота сечения балки и его прогиб с интервалом в 1 метр.

Запишем зависимости угла поворота сечения с заданным интервалом:

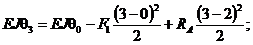
Ниже приводятся зависимости для расчета прогиба балки:

Результаты расчетов сведены в таблицу 2.1.

Таблица 2.1

x	0	1	2	3	4	5	6	7	8	9
EJ θ	4,52	3,02	–1,48	–6,13	–8,83	–5,23	–0,43	6,14	10,1	18,9
EJy	–5,04	–1,02	0,0	–4,03	–11,6	–16,2	–21,7	–19,3	–9,06	0,0

 

Максимальное значение по абсолютной величине кНм ³. Определим максимальный прогиб 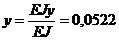  м, что превышает допустимое значение. Условие жесткости такого двутавра не выполняется, следовательно, необходимо подобрать двутавр большего сечения.

Так для двутавра № 12 J_z =350 см ⁴,

м < [ y ].

Разделим данные таблицы 2.1 на жесткость двутавра № 12 и получим прогибы балки (в сантиметрах) и углы поворота ее сечений (в градусах). Результаты представлены в таблице 2.2.

                                                                      Таблица 2.2

x	0	1	2	3	4	5	6	7	8	9
θ	0,35	0,24	–0,12	–0,48	–0,69	–0,41	–0,03	0,38	0,79	1,47
y	–0,68	–0,14	0,0	–0,55	–1,58	–2,20	–2,95	–2,62	–1,23	0,0

 

Графический результат расчетов показан на рисунке 2.9.

Координата максимального прогиба совпадает с координатой нулевого угла поворота сечения. Эту координату (x_m) определяют путем интерполяции соседних точек функции θ. Для приведенного примера x_m =6,073 м. Этой координате соответствует максимальный прогиб 2,7 см. Условия жесткости выполнены.

 

Рис. 2.9

 

Метод начальных параметров позволяет построить эпюры внутренних усилий с помощью следующих соотношений:

,

.

При построении эпюр внутренних усилий необходимо иметь в виду, что точки приложения сосредоточенных сил и моментов необходимо просчитывать дважды: слева и справа от заданной координаты приложения сосредоточенного момента или сосредоточенной силы, соответственно.

По приведенным соотношениям легко проверить правильность выполнения задания, поставленного в РР № 3, и выполненного согласно рисунку 2.9.

 

3. Определим прогиб балки в точке С, расположенной на координате x =7 м, и угол поворота сечения методом перемножения эпюр (способом Верещагина).

Для определения перемещения точки необходимо в ней приложить силу, равную единице и построить эпюру изгибающих моментов. Для определения угла поворота сечения в данной точке прикладывают изгибающий момент, равный единице, и строят эпюру изгибающих моментов.

Результаты предварительных решений представлены на рисунке 2.10.

Если одна из эпюр криволинейна, то интеграл произведения внутренних усилий можно вычислить по формуле численного интегрирования Симпсона

.

Если обе эпюры прямолинейны, то

.

Прогиб балки в точке С и угол поворота сечения в этой точке определяются путем перемножения эпюр на всех пяти участках балки, то есть

Рис. 2.10

 

Получим:

, ,

,

,

.

Отсюда   м, или 2,95 см, что совпадает с первым решением методом начальных параметров. Аналогично:

,

,

,

,

.

.

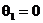Ошибка в определении угла поворота сечения составляет менее 3%, так как угол практически равен нулю.

 

 

РАСЧЕТНАЯ РАБОТА № 5.

ПОСТРОЕНИЕ ЯДРА СЕЧЕНИЯ

Для колонны с поперечным сечением (рис. 2.11) построить эпюру нормальных напряжений и ядро сечения по известным координатам полюса; определить положение нулевой линии; вычислить допускаемую величину сжимающей силы F, приложенной в полюсе, если [σ]=4 мПа; R_р =0,4 мПа. Построить пространственную эпюру «σ». Размеры сечения на рисунке 2.11 даны в сантиметрах.

Решение

1. Определим центр тяжести сечения.

Разобьем сечение сложной формы на: прямоугольник 180×80 см (фигура 1) и два выреза 80×30 см (фигуры 2 и 3). Проводим вспомогательные оси Oyz. Площади сечений и координаты их центров масс, соответственно равны:

Координаты центра масс сечения:

Проводим центральные оси инерции Cz_cy_c.

 

2. Определим моменты инерции сечения.

Собственные моменты инерции фигур 1, 2 и 3 вычисляем по формулам :

 

Рис. 2.11

Пересчитаем частные моменты инерции относительно центральных осей. Расстояния между осями:

Имеем: 

,

,

, ,

.

Суммарные значения моментов инерции заданного сечения:

, ,

.

 

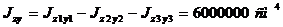3. Определим положение главных центральных осей инерции и главные моменты инерции.

, ,

,

 

4. Определим квадраты главных центральных радиусов инерции сечения:

5. Построим ядро сечения.

Расчеты сведены в таблицу 2.3, где z_F и y_F – координаты шести выступающих точек сечения (точек приложения вертикальной нагрузки) в системе центральных осей Cy_cz_c. Координаты этих же точек в системе главных центральных осей симметрии пересчитываются по формулам:

Координаты нейтральных линий для соответствующих точек сечения определим по следующим зависимостям:

                                                                           Таблица 2.3

№ п/п

Координаты

Расчетных

точек в осях ZY, (см)