Перемещение от динамической нагрузки определяется по формуле
. (9.7)
Динамический коэффициент при ударе
. (9.8)
Динамическое напряжение 
.
Задачи
9.6. Стальной стержень диаметром 25 мм и длиной 1,5 м растянут внезапно приложенной постоянной силой 2500 кг. Определить наибольшие напряжение и деформацию.
Ответ: 1020 кг / см 2 (102·106 Па); 0,765 мм (0,765·10–3 м).
9.7. Вертикальный стержень, статически сжатый силой F, укорачивается на 2 мм. Определить наибольшее укорочение стержня, если этот же груз сожмет его, падая с высоты 1 мм.
Ответ: 4,83 мм (0,00483 м).
9.8. Груз 45 кг падает с высоты 10 см на балку, которая от этого удара прогибается на 2,5 см. Какая статическая нагрузка, приложенная в том же сечении балки, вызовет тот же прогиб?
Ответ: 450 кг (4500 Н).
9.9. Деревянная балка с прямоугольным сечением 
см подверглась изгибающему удару силой F =100 кг в сечении В. Наибольший прогиб балки в сечении D при ударе оказался равным 6 мм. Определить высоту падения груза и наибольшее нормальное напряжение в балке. Е =105 кг / см 2.
Ответ: 1,96 см (0,0196 м); 80 кг / см 2 (8·106 Па).
9.10. Один конец двутавровой балки № 16 длиной 3 м опирается на жесткую шарнирную опору, второй – на стальную цилиндрическую винтовую пружину, имеющую 10 витков при среднем диаметре витка 10 см и диаметре проволоки 20 мм.
С какой высоты Н может упасть на балку груз F =200 кг, не вызывая в балке и пружине напряжений, превышающих допускаемые напряжения, если [σ]=1600 кг / см 2 (для материала балки) и [τ]=2000 кг / см 2 (для материала пружины)?
Ответ: 4 см (0,04 м).
РАЗДЕЛ 2
СБОРНИК КОНТРОЛЬНЫХ ЗАДАНИЙ
В данном разделе приводится необходимый минимум контрольных заданий, решение которых входит в обязательный контроль успеваемости студентов. Комплекс контрольных заданий охватывает наиболее важные разделы изучаемой дисциплины, необходимые для освоения инженеру–строителю. В качестве помощи для самостоятельной работы студента к каждому заданию прилагается подробный пример решения задачи.
РАСЧЕТНАЯ РАБОТА № 1.
ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК ПЛОСКИХ СЕЧЕНИЙ
Определить геометрические характеристики в сечении, состоящем из стальных прокатных профилей и прямоугольной пластины, показанных на рисунке 2.1.
Решение
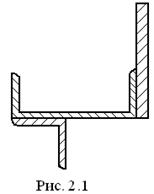Сечение состоит из равнобокого уголка 70×70×8, швеллера № 22а и прямоугольника 180×20.
1. Определим характеристики сечений каждого элемента, используя таблицы сортаментов прокатных профилей.
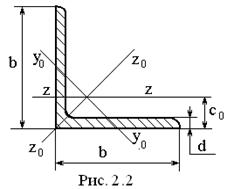
На рисунке 2.2 показан равнобокий уголок, для которого b =7 см, площадь поперечного сечения А =10,67 см2, моменты инерции Jy = Jz =48,16 см4, Jmin =20,0 см4, с 0=2,46 см. Дадим данному элементу номер 1.
Под номером 2 выпишем элементы сечения швеллера № 22а (рис. 2.3): А =28,8 см2, Jz =2330 см4, Jy =187 см4, z 0=2,46 см.
Для прямоугольника (обозначим данный элемент под номером 3):
А=36 см2,
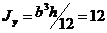см4,
см4.
2. Построим в масштабе общую схему заданного поперечного сечения (рис. 2.4) и окончательное определение характеристик поперечных сечений отдельных элементов общей конструкции.
Уголок (элемент 1, рис. 2.2):
А 1=10,67 см2, J' z 1= J' y 1=48,16 см4,
J' min =20 см4,
J' z 1 y 1=–28,16 см4, zc 1=4,98 см, yc 1=4,98 см.
Общая формула для определения центробежного момента любого уголка имеет вид
.
Знак полученного результата зависит от положения концов уголка в тех или иных квадрантах декартовых координат.
Швеллер (элемент 2, рис. 2.3):
А 2=28,8 см2, J'z 2=187 см4, J'y 2=2330 см4, J'z 2 y 2=0, zc 2=11 см, yc 2=9,46 см.
В данном случае швеллер в таблице сортаментов представлен в вертикальном положении, а на общей схеме он развернут горизонтально. Следовательно, в моментах инерции относительно осей необходимо поменять местами их численные значения.
Прямоугольник (элемент 3):
А 3=36 см2, J'z 3=972 см4, J'y 3=12 см4, J'z 3 y 3=0,
zc 3=23 см, yc 3=16 см.
3. Определим центр масс сечения и построим центральные оси инерции. По полученным значениям наносим положение центра тяжести сечения и проводим центральные оси z 0 и y 0 (рис. 2.4):
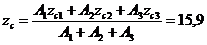см;
см.
4. Определим расстояния между центральными осями инерции сечения и осями инерции отдельных элементов:
см; 
см;
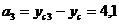см; 
см;
см; 
см.
5. Пересчет моментов инерции отдельных элементов сечения относительно центральных осей инерции:
;
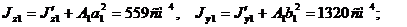
6. Моменты инерции сечения находим путем суммирования моментов инерции отдельных элементов системы:
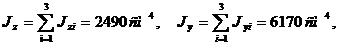
7. Определим направления главных центральных осей инерции:
; 
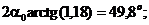
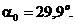
Откладываем найденное значение угла α против часовой стрелки и проводим главные центральные оси инерции U (ось максимального момента инерции) и V (ось минимального момента инерции).
8. Вычислим главные центральные моменты инерции
.
После подстановки значений получим:
9. Определим координаты эллипса инерции.
Здесь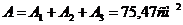 
общая площадь поперечного сечения системы.
Полученные значения радиусов инерции откладываются на соответствующих осях U и V для проведения контура эллипса инерции (на рисунке 2.4 эллипс не показан).
Рис. 2.4
РАСЧЕТНАЯ РАБОТА № 2.
