Внутренние усилия, действующие в поперечном сечении бруса, определяются по значениям внешней нагрузки с левой или правой стороны от сечения.
, 
, 
.
(5.1)
Максимальные нормальные и касательные напряжения при прямом изгибе соответственно равны
. (5.2)
Потенциальная энергия деформации при изгибе
(5.3)
Задачи
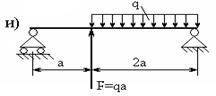
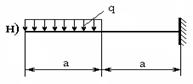
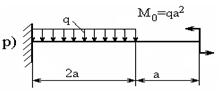
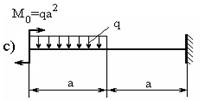
5.1. Построить эпюры поперечных сил и изгибающих моментов для балок, изображенных на рисунках 5.1–5.2.
| 
|
| 
|
| 
|
| 
|
| 
|
| Рис. 5.1. | |
| 
|
| 
|
| 
|
| 
|
Рис. 5.2.
ОПРЕДЕЛЕНИЕ ДЕФОРМАЦИЙ ПРИ ИЗГИБЕ
Аналитический способ определения деформаций
Основное дифференциальное уравнение изогнутой оси балки
. (6.1)
Задачи
6.1. Стержень длиной 1 м и сечением 
см, защемленный одним концом, изгибается парой сил с моментом 10 кг·м, приложенным на другом конце. Найти величину модуля упругости материала и радиус кривизны оси балки, если угол поворота концевого сечения равен θ=0,0375.
Ответ: Е =2·106 кг / см 2 (2·1011 Па); ρ =26, 8 м.
6.2. Балка пролетом 2 м, лежащая на двух опорах, изогнута по дуге круга. Ее прогиб посредине пролета равен 0,5 см. При Е =105 кг / см 2 и J =230 см 4 определить радиус кривизны изогнутой оси балки и величину изгибающего момента.
Ответ: ρ =100 м; М =2300 кг·см (2300 кН·м).
6.3. Путем интегрирования дифференциального уравнения упругой линии найти угловые и линейные перемещения свободного конца балки, защемленной одним концом.
| 
|
| 
|
Ответ:
a) 
б) 
в) 
г) 
Метод начальных параметров
Выражения для углов поворота и прогибов при изгибе для любого сечения имеют вид:
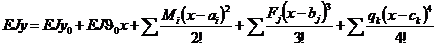(6.2)
Задачи
6.4. Пользуясь методом начальных параметров найти угловые и линейные перемещения свободного конца балки. Принять условия задачи 6.3.
Энергетический способ определения деформаций
В случае плоской задачи выражение для определения перемещений (формула Мора) имеет вид:
(6.3)
Правило Верещагина вычисления интегралов
(6.4)
Задачи
6.5. Найти угловые и линейные перемещения свободного конца балки, применяя способ Верещагина. Принять условия задачи 6.3.
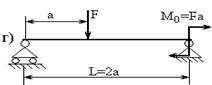
6.6. Определить величину прогибов посредине пролета и углов поворота опорных сечений для балок, показанных на рисунках, используя способ Верещагина.
| 
|
| 
|
Ответ: а)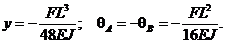 
б) 
в) 
г) 
| 
| 
|
6.7. Для приведенных схем нагружения рамы постоянного сечения из стали (Е=2·106 кг / см 2) определить величину вертикального перемещения y, горизонтального перемещения Δ и угла поворота θ свободного конца.
Ответ: а) 
б) 
в) 
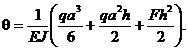
СЛОЖНОЕ СОПРОТИВЛЕНИЕ
Косой изгиб
Полный изгибающий момент связан с его составляющими зависимостями
(7.1)
Угол наклона нейтральной линии к оси z
. (7.2)
Напряжения в крайних точках сечения рассчитывается по формуле
. (7.3)
Задачи
7.1. Какое положение займет нейтральный слой в балке прямоугольного поперечного сечения, если плоскость действия нагрузки будет совпадать с одной из диагональных плоскостей?
Ответ: Совпадает с другой диагональной плоскостью.
| 
|
7.2. Деревянная балка длиной 2 м, имеющая прямоугольное поперечное сечение 
см, защемлена одним концом и нагружена сосредоточенной силой 240 кг на другом конце. Нагрузка лежит в плоскости поперечного сечения балки и проходит через его центр тяжести. Построить эпюры нормальных напряжений по сторонам защемленного сечения и определить полный прогиб свободного конца балки.
Ответ: σА=2 кг / см 2 (0,2·106 Па); σВ=102 кг / см 2 (10,2·106 Па); σС=–2 кг / см 2 (–0,2·106 Па); σD=–102 кг / см 2 (–10,2·106 Па).
7.3. Деревянная балка длиной 2 м, защемленная одним концом, изгибается силами F 1 и F 2. Подобрать прямоугольное сечение балки с отношением высоты к ширине, равным 2, и определить полный прогиб ее в сечении А по величине и направлению. [σ]=100 кг / см 2.
Ответ: 
см (0,09×0,18 м; f =1,98 см (0,0198 м) (под углом 810 к вертикали).
