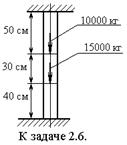
2.6. Стержень с площадью поперечного сечения А =10 см 2 жестко защемлен двумя концами и нагружен, как указано на рисунке. Определить напряжений во всех трех участках стержня.
Ответ: σв=1083 кг / см 2 (108,3·106 Па), σср=83 кг / см 2 (8,3·106 Па), σн=–1417 кг / см 2 (–141,7·106 Па).
2.7. Жесткий брус закреплен с помощью системы стальных стержней одинакового поперечного сечения. Принимая [σ]=1600 кг / см 2, определить площадь поперечного сечения стержней.
Нагрузка F =16000 кг.
Ответ: а) 8 см 2 (8·10–4 м 2), б) 20 см 2 (20·10–4 м 2).
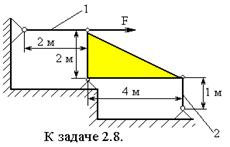2.8. Жесткая конструкция прикреплена к фундаменту при помощи шарнира и двух стержней. Стержень 1 – стальной ([σc]=1600 кг / см 2), стержень 2 – чугунный ([σч]=1000 кг / см 2). Их площади сечений равны: Aс =30 см 2, Aч =50 см 2.
Определить максимальную нагрузку F.
Ответ: F=112500 кг (1,125 мН).
Учет собственного веса
2.9. Определить размеры в плане ступенчатого столба квадратного поперечного сечения высотой 30 м, имеющего три участка одинаковой длины, сжатого силой F =60000 кг. Допускаемое напряжение для кладки столба на сжатие [σ]=10 кг / см 2, удельный вес ее равен γ=0,002 кг / см 3. Построить эпюру распределения напряжений по длине стержня.
Ответ: 87 
87 см (0,87×0,87 м), 97 97 см 0,97×0,97 м),
108 108 см (1,08×1,08 м).
2.10. Стальной стержень подвешен вертикально за верхний конец и нагружен только собственным весом. Если напряжение не должно превышать 300 кг / см 2 и удельный вес стали равен γ=0,00785 кг / см 3, то какова наибольшая допустимая длина стержня? Построить эпюру распределения напряжений по длине стержня.
Ответ: 382 м.
2.11. Определить полное удлинение стального стержня длиной 120 м, вызванное собственным весом. Заданы: γ=0,00785 кг / см 3, Е =2·106 кг / см 2.
Ответ: 2,8 мм (0,0028 м).
| 
| 
|
2.12. Определить с учетом собственного веса перемещение свободного конца показанного на рисунке стержня, если его поперечное сечение А, модуль упругости Е, а объемный вес материала γ.
Ответ: 
.
2.13. Стержень длиной L и площадью поперечного сечения А, выполненный из материала с удельным весом γ, защемлен, как показано на рисунке, своим верхним и нижним концами. Определить напряжения в верхнем и нижнем сечениях стержня, вызванные его собственным весом, и начертить эпюру распределения напряжений по длине стержня.
Ответ: 
ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
При двухосном напряженном состоянии напряжения, действующие по наклонной площадке, равны:
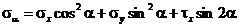, (3.1)
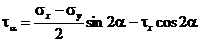. (3.2)
Угол наклона главной площадки к площадке, в которой действует напряжение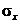 
, определяется по формуле
, (3.3)
а главные напряжения на этих площадках
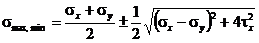. (3.4)
Экстремальные касательные напряжения и положение их площадок находятся по формулам:
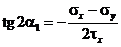, (3.5)
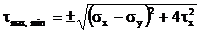. (3.6)
Задачи
3.1. Стержень диаметром 7,5 см растянут силами 35000 кг. Определить полное напряжение в поперечном сечении; определить полное и касательное напряжения в сечении с нормалью, наклоненной под углом 15о к оси стержня.
Ответ: σ0=795 кг / см 2 (79,5·106 Па), рα=767 кг / см 2 (76,7·106 Па), τα=198 кг / см 2 (19,8·106 Па).
3.2. В растянутом стержне нормальные напряжения по одной из наклонных площадок равны 700 кг / см 2, а касательные 500 кг / см 2. Определить наибольшие нормальные и касательные напряжения.
Ответ: σmax=1056 кг / см 2 (105,6·106 Па), τmax=52,8·106 Па.
3.3. По заданным σ1 и σ2 определить аналитически и графически σα, τα и полное напряжение р α в сечении под углом α к сечению, на которое действует σ1.
а) σ1=800 кг / см 2, σ2=–500 кг / см 2, α=600;
б) σ1=750 кг / см 2, σ2=–750 кг / см 2, α=600;
в) σ1=150 кг / см 2, σ2=150 кг / см 2, α=600.
Ответ: а) σα=–175 кг / см 2 (–17,5·106 Па),
б) σα=–375 кг / см 2 (–37,5·106 Па), 
в) σα=150 кг / см 2 (15·106 Па).
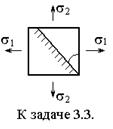
3.4. Определить графически (с помощью круга напряжений) величину и направление главных напряжений для показанных на рисунке элементов и изобразить внутри них элементы, находящиеся под действием лишь главных напряжений.
Ответ: а) 440 кг / см 2 (44·106 Па),
б) 625 кг / см 2 (62,5·106 Па).
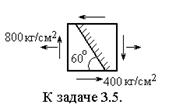
3.5. По заданным напряжениям (см. рисунок) определить графически σα и τα в указанном наклонном сечении.
Ответ: σα=258 кг / см 2 (25,8·106 Па), τα=546 кг / см 2 (54,6·106 Па).
СДВИГ И КРУЧЕНИЕ
Сдвиг
Касательное напряжение при сдвиге (срезе) определяется по формуле
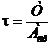, (4.1)
где Т – поперечное усилие; Аср – площадь среза.
Нормальные напряжения смятия при поперечной нагрузки определяются по формуле
, (4.2)
где Асм – площадь смятия всех элементов.
Закон Гука при сдвиге
. (4.3)
Здесь G – модуль упругости при сдвиге; γ – относительная угловая деформация.
Работа внешних сил, равная энергии деформации рассчитывается по формуле
. (4.4)
Площадь среза сварочного шва
, (4.5)
где δ – толщина листа, L – длина сварочного шва.
Задачи
4.1.Определить необходимое количество заклепок диаметром 17 мм для соединения впритык двух листов при помощи двух накладок. Растягивающая сила F =30000 кг. Толщина листов 10 мм, толщина накладок 6 мм. Допускаемые напряжения: на срез [τ]=1000 кг / см 2, на смятие [σ]=2800 кг / см 2.
Ответ: Семь заклепок с каждой стороны стыка.
4.2. Два листа соединены при помощи одной накладки. Толщина листов и накладки по 10 мм. Определить необходимое количество заклепок диаметром 17 мм, если допускаемые напряжения: на срез [τ]=1400 кг / см 2, на смятие [σ]=3200 кг / см 2. Сила F, растягивающая соединение, равна 24000 кг.
Ответ: Восемь заклепок с каждой стороны стыка.
4.3. В стыке двух листов применены заклепки диаметром 26 мм. Соединение выполнено, как показано на рисунке. Допускаемые напряжения: [τ]=1000 кг / см 2, [σс]=2800 кг / см 2, [σ]=1600 кг / см 2. Толщина: накладки – 10 мм, листов – 25 мм. Определить наибольшее растягивающее усилие, допускаемое для данного стыка.
Ответ: 25000 кг (250 кН).
4.4. Определить минимальную длину x, необходимую для приварки листа в соединении, изображенном на рисунке, если растягивающее напряжение в листе равно 1400 кг / см 2, а допускаемое напряжение на срез для сварки [τв]=800 кг / см 2.
Ответ: 7,5 см (0,075 м).
4.5. Определить необходимую длину x фланговых швов для соединения внахлестку двух листов разной ширины.
Усилие, испытываемое соединением, F =15000 кг. Допускаемое напряжение на срез для сварки равно 1100 кг / см 2. Толщина узкого листа 10 мм, а широкого – 8 мм.
Ответ: 10 см (0,1 м).
Кручение круглых стержней
Определение крутящих моментов по потребляемой мощности:
, (4.6)
если мощность N задается в киловаттах,
, (4.7)
если мощность задается в лошадиных силах.
Наибольшие касательные напряжения
. (4.8)
Относительный угол скручивания
. (4.9)
Абсолютная деформация при кручении
. (4.10)
Работа внешних сил, равная энергии деформации рассчитывается по формуле
. (4.11)
Задачи
4.6. Определить диаметр сплошного вала, передающего 450 л.с. при 300 об / мин. Угол закручивания не должен превышать 10 на 2 м длины вала, а наибольшее касательное напряжение 400 кг / см 2; 
кг / см 2.
Ответ: 11,2 см (0,112 м).
4.7. Определить наименьший диаметр стального вала, передающего 18 л.с. при 120 об / мин, если допускаемый угол закручивания равен 10 на длине, равной 15 диаметрам вала. Как велики при этом будут наибольшие касательные напряжения? кг / см 2.
Ответ: 4,9 см (0,049 м); 466 кг / см 2 (46,6*106 Па).
4.8. Сплошной вал диаметром 10 см и длиной 6 м закручен на угол 40. Чему равно наибольшее касательное напряжение, если кг / см 2?
Ответ: 466 кг / см 2 (16,6*106 Па).
4.9. Определить наибольшие касательные напряжения в сечениях АА и ВВ вала при М 1=13000 кг·см; М 2=30000 кг·см. Диаметр вала в сечении АА 5 см, в сечении ВВ 7,5 см.
Ответ: τА=530 кг / см 2 (53·106 Па), τВ=205 кг / см 2 (20,5·106 Па).
4.10. Определить наибольший крутящий момент, который может быть приложен к стальному стержню диаметром 10 мм, если допускаемое напряжение не должно превосходить1500 кг / см 2. Какова наименьшая длина стержня, если угол закручивания равен 900; G =8·105 кг / см 2?
Ответ: Мкр =295 кг·см (295 кН·м); L =418 см (4,18 м).
4.11. Концы круглого стержня жестко защемлены, как показано на рисунке. В промежуточном сечении стержня приложена пара сил с моментом 1200 кг·м. Определить наибольшие касательные напряжения, если диаметр вала 8 см.
Ответ: 795 кг / см 2 (79,5·106 Па).
4.12. Круглый стержень с жестко защемленными концами подвергается действию двух равных и одинакового направленных пар сил с моментами по 800 кг·м. Определить угол поворота среднего сечения 1–1, если диаметр вала равен 10 см. Расстояния а =60 см; b =80 см.
Ответ: 0,340 (0,006 рад).
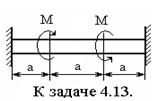4.13. К круглому стержню с жестко закрепленными концами приложены две равные и противоположно направленные пары сил с моментами по 1000 кг·м. Определить диаметр вала, если допускаемое касательное напряжение равно 600 кг / см 2.
Ответ: 8,25 см (0,0825 м).
Винтовые пружины
Наибольшие напряжения при деформации пружин
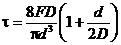. (4.12)
Здесь D – диаметр пружины, d – диаметр проволоки. Деформация пружины при действии внешней силы F равна
. (4.13)
Жесткость пружины
. (4.14)
Задачи
4.14. Цилиндрическая винтовая пружина, изготовленная из 6–миллиметровой проволоки, имеет 20 витков со средним радиусом 7,5 см. Определить осевую растягивающую нагрузку, которая может быть допущена на пружину, если касательное напряжение в ней не должно превосходить 900 кг / см 2. Чему при этом будут равны удлинение пружины и наибольшая удельная работа деформации? G =8·105 кг / см 2.
Ответ: 5 кг (50 Н); 26 см (0,26 м); 0,24 кг·см / см 3 (240·106 Дж/м 3).
4.15. Винтовая пружина должна быть спроектирована так, чтобы ее жесткость равнялась 40 кг / см, а полная осадка при соприкосновении витков равнялась 4 см. Средний диаметр витков равен 6 см. Допускаемое касательное напряжение на срез 1400 кг / см 2. Определить диаметр стальной проволоки, число витков и просвет между витками в ненагруженном состоянии.
Ответ: 12,5 мм (0,0125 м); 28 витков; 1,43 мм (0,00143 м).
ПЛОСКИЙ ИЗГИБ
