Нормальное напряжение, равномерно распределенное по поперечному сечению стержня, определяется по формуле
, (2.1)
где N – осевое внутреннее усилие;
А – площадь поперечного сечения стержня.
До предела упругости напряжение пропорционально относительной деформации (закон Гука), то есть
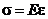. (2.2)
где Е – модуль упругости (характеристика материала);
– отношение абсолютной продольной деформации к начальной длине стержня.
Закон Гука также может быть представлен в виде
. (2.3)
Произведение EА называется жесткостью стержня. Удлинение бруса под действием собственного веса равно
, (2.4)
где G – сила веса.
Отношение поперечных деформаций к продольным при растяжении (сжатии) называется коэффициентом Пуассона.
. (2.5)
В сечениях, наклонных к продольной оси стержня, нагруженного на концах осевыми усилиями, возникают как нормальные, так и касательные напряжения, пропорциональные модулю упругости второго рода G (модуль сдвига). Модуль упругости Е, модуль сдвига G, коэффициент Пуассона μ являются характеристиками материала. Их значения приводятся в таблице 1.1.
Работа внешних сил, равная энергии деформации рассчитывается по формуле
. (2.6)
Потенциальная энергия деформации бруса от собственного веса
. (2.7)
Таблица 1.1
| Наименование материала | E (Па) | G (Па) | μ |
| Чугун Углеродистые стали Алюминий катанный Стекло Камень известняк Дерево вдоль волокон Дерево поперек волокон Бетон класса В10…В60 Кирпичная кладка | (1,2–1,6)·1011 (2–2,1)·1011 0,9·1011 0,56·1011 0,42·1011 0,11·1011 (0,5–0,1)·1011 (0,18–0,4)·1011 0,03·1011 | 0,45·1011 0,81·1011 0,27·1011 0,22·1011 ––– 0,006·1011 ––– (0,07–0,16)·1011 ––– | 0,23…0,27 0,24…0,28 0,32…0,36 0,25 ––– ––– ––– 0,2 ––– |
Задачи
2.1. Определить напряжения во всех участках изображенного на рисунке стального стержня и полную его деформацию, если поперечное сечение равно 10 см 2.
Ответ: в левом участке σ=400 кг / см 2 (40·106 Па); в среднем – σ =0; в правом – σ =–200 кг / см 2 (–20·106 Па).
2.2. На рисунке представлен стержень, верхняя часть которого стальная, а нижняя чугунная. Осевая нагрузка F укорачивает весь стержень на 0,2 мм. Определить величину нагрузки F.
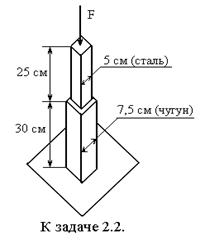Ответ: 21200 кг (212 кН).
2.3. Жесткий брус АВ, деформацией которого можно пренебречь, горизонтально подвешен на тягах 1 и 2. Тяга 1 – стальная, круглого сечения, диаметром 20 мм, тяга 2 – медная, тоже круглого сечения, диаметром 25 мм. На каком расстоянии а от узла А нужно поместить груз F, чтобы после деформации тяг брус АВ остался горизонтальным? Чему в этом случае будут равны напряжения в тягах, если F =3000 кг?
Ответ: а =1,08 м,
σ1=440 кг / см 2 (44·106 Па), σ2=330 кг / см 2 (33·106 Па).
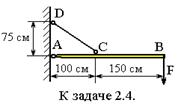2.4. Жесткий стержень АВ нагружен силой F и поддерживается стальной тягой С D круглого поперечного сечения диаметром 20 мм. Определить наибольшую допустимую нагрузку F и опускание точки В. Допускаемое напряжение для материала стержня CD равно 1600 кг / см 2.
Ответ: F =1200 кг (12 кН), δВ=4,17 мм (0,00417 м).
2.5. Груз подвешен к стальной проволоке, размеры которой до деформации были следующими: L =3 м и d =1,6 мм. Удлинение проволоки оказалось равным 1,5 мм. Затем тот же груз был подвешен к медной проволоке длиной L 1=1,8 м и диаметром d 1=3,2 мм. Ее удлинение получилось равным 0,39 мм. Определить модуль упругости медной проволоки, если модуль стальной – Е =2·106 кг / см 2.
Ответ: 1,15·106 кг / см 2 (1,15·1011 Па).
