Геометрические характеристики

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

НАЦИОНАЛЬНАЯ АКАДЕМИЯ ПРИРОДООХРАННОГО И КУРОРТНОГО СТРОИТЕЛЬСТВА

 

 

В.Т. Чемодуров, Э.В. Литвинова, А.Г. Попов, А.С. Маслак

 

СБОРНИК ЗАДАЧ И РАСЧЕТНЫХ РАБОТ

ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ

 

Учебное пособие

Симферополь – 2014

УДК 539.2

 

 

В.Т. Чемодуров, Э.В. Литвинова, А.Г. Попов, А.С. Маслак.

Сборник задач и расчетных работ по сопротивлению материалов (для студентов всех специальностей дневной и заочной форм обучения): Учебное пособие. – Симферополь: НАПКС, 2014. – 93 с.

 

 

Рецензенты:

- кандидат технических наук, доцент кафедры технологии строительных конструкций и строительных материалов НАПКС Любомирский Н.В.;

- кандидат технических наук, доцент кафедры железобетонных конструкций НАПКС Жигна В.В.

 

 

Одобрено и рекомендовано к печати Учебно–методическим советом НАПКС «___» _____________ 2014 г. Протокол № ___.

 

 

Рассмотрено и одобрено на заседании кафедры механики и сейсмостойкости сооружений «03» февраля 201 4 г. Протокол № 7.

 

Учебное пособие предназначено для усвоения теоретических знаний классического курса сопротивления материалов и приобретения студентами ВУЗов строительного профиля практических навыков в определении внутренних усилий в конструкциях; расчете на прочность, жесткость и устойчивость брусьев при заданной внешней нагрузке.

В первом разделе пособия приведены задачи, соответствующие учебной программе курса «Сопротивление материалов»: простое и сложное сопротивление, определение перемещений в упругих системах, продольный и продольно–поперечный изгиб прямого стержня, основы расчета брусьев на динамическую нагрузку. Второй раздел пособия включает примеры выполнения заданий расчетных работ. В приложении приведены варианты заданий расчетных работ.

Выработка навыков в решении приведенных задач позволит подготовить студентов к самостоятельному анализу проблем, выдвигаемых практикой работы в соответствующей области деятельности, а также к изучению специальной литературы по более сложным вопросам.

Большая часть задач сформулирована с расчетом их использования для проведения контрольных работ и индивидуальных домашних заданий. Каждый раздел начинается с краткой информации по теории вопроса.

При овладении курса «Сопротивление материалов» необходимо добиться развития системы навыков самостоятельной творческой работы, умения анализировать полученные результаты. Эти качества достигаются путем самостоятельного решения задач и расчетных заданий, приведенных в данном сборнике.

 

УСЛОВНЫЕ ОБОЗНАЧЕНИЯ

x, y, z – прямоугольные координаты

а, b, L, h, r, d – размеры

i_x, i_y, i_z – радиусы инерции

ρ – радиус кривизны

J_x, J_y, J_z – осевые моменты инерции

J_p – полярный момент инерции

W_x, W_y, W_z – осевые моменты сопротивления

W_p – полярный момент сопротивления

S_x, S_y, S_z – статические моменты сечения

А – площадь поперечного сечения, возможная работа внешних сил

G – вес, модуль сдвига

Е – модуль упругости первого рода

m – масса

γ – удельный вес, угол сдвига

F – сосредоточенная сила

q – распределенная нагрузка

М – сосредоточенный момент

P – обобщенная сила

M_y, M_z – изгибающие моменты

М_кр – крутящий момент

Q_y, Q_z – поперечные силы

N – продольная сила

Ω – площадь эпюры

 

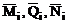 – внутренние усилия от единичной нагрузки

 – внутренние усилия от заданной нагрузки

U – потенциальная энергия

φ – угловой путь, угол закручивания

 – относительный угол закручивания

ω – угловая скорость

ε – угловое ускорение

g – ускорение силы тяжести

f – частота колебаний

Т – период колебаний

t – время

n – число оборотов в минуту

р – давление

Δ – абсолютная деформация

ε_x, ε_y, ε_z – относительные линейные деформации

γ _yz – относительная угловая деформация

σ – нормальное напряжение

τ – касательное напряжение

μ – коэффициент Пуассона

[σ], [τ] – допускаемые напряжения

σ_в – предел прочности

σ_т – предел текучести

λ – гибкость  

РАЗДЕЛ 1

СБОРНИК ЗАДАЧ

В данном разделе приведен необходимый минимум практических задач, по своему содержанию охватывающий все разделы изучаемого курса. Тщательная проработка задач данного раздела позволит студентам успешно сдать семестровые экзамены.

 

ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ

ПЛОСКИХ СЕЧЕНИЙ

Площадь – простейшая геометрическая характеристика поперечного сечения. Если представить сечение состоящим из бесконечного множества элементарных площадок dА (рис. 1.1), то площадь всего сечения

.           (1.1)

Статические моменты площади фигуры относительно координатных осей y и z равны:

 (1.2)

Координаты центра тяжести плоской фигуры определяются по формулам

                   (1.3)

Моменты инерции плоской фигуры относительно осей y и z равны:

          (1.4)

Центробежный момент инерции относительно тех же осей

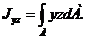                          (1.5)

Полярный момент инерции относительно какой–либо точки, например, начала координат

                   (1.6)

Оси y и z, проходящие через центр тяжести фигуры, называются центральными осями инерции. При переходе от центральных осей инерции к параллельным осям y ₁ и z ₁ (рис. 1.2) моменты инерции относительно новых координат составят:

(1.7)

При повороте координатных осей на угол α (рис. 1.3) моменты инерции относительно повернутых осей составят

          (1.8)

          (1.9)

            (1.10)

 

Главными моментами инерции являются наибольший и наименьший моменты инерции фигуры. Они определяются по формуле

         (1.11)

Радиусы инерции сечения относительно осей вычисляются по формулам

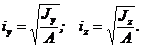                          (1.12)

Задачи

1.1. Определить момент инерции относительно оси z сечения, изображенного на рисунке. Размеры показаны в мм.

Ответ: J_z =3167 см ⁴ (3167·10^–8 м ⁴).

 

1.2. Как изменятся площадь и момент инерции J_z трубчатой балки, изображенной на первом рисунке, если заменить одно отверстие диаметром 20 см – двумя, диаметром каждое по 10 см, расположенными, как показано на втором рисунке?

Ответ: площадь увеличится на 38,6%, а момент инерции уменьшится на 2%.

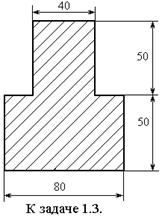
1.3. Найти момент инерции площади таврового сечения, изображенного на рисунке, относительно центральной оси Oz₀, параллельной основанию. Размеры даны в мм.

Ответ: J_z =458 см ⁴ (458·10^–8 м ⁴).

 

1.4. Найти положение главных центральных осей инерции и вычислить значения главных моментов инерции для сечений, изображенных на рисунке. Размеры даны в мм.

Ответ: а) α=14,3^о, J_min =15,7 см ⁴ (15,7·10^–8 м ⁴), J_max =150 см ⁴ (150·10^–8 м ⁴); б) α=6,3^о, J_y =6930 см ⁴ (6930·10^–8 м ⁴), J_z =69700 см ⁴ (69700·10^–8 м ⁴).

РАСТЯЖЕНИЕ И СЖАТИЕ