Раздел VII
При исследовании многих явлений в различных областях науки (физика, химия, биология, экономика и т.д.) не всегда удается найти прямую связь между интересующими нас величинами, а удается найти связь между их производными или дифференциалами. Тогда с математической точки зрения приходится иметь дело с дифференциальными уравнениями.
Пример 7.1. Как известно, радиус-вектор 
при движении тела массой 
под действием силы 
на основании второго закона Ньютона удовлетворяет уравнению
(7.1)
Чтобы найти траекторию движения тела (функцию 
), нужно решить уравнение (7.1).
Пример 7.2. В простой экономической модели воспроизводства Калецкого запас наличного капитала в зависимости от времени 
удовлетворяет следующему уравнению
(7.2)
где 
Пример 7.3. Потенциал электростатического поля неподвижных зарядов в трехмерной декартовой системе координат удовлетворяет уравнению Пуассона
(7.3)
где 
плотность зарядов.
Определение 7.1. Уравнение, в котором неизвестная функция находится под знаком производной или дифференциала, называется дифференциальным уравнением. В этом смысле уравнения (7.1) – (7.3) есть примеры дифференциальных уравнений.
Определение 7.2. Если неизвестная функция в дифференциальном уравнении зависит от одной независимой переменной, то такое уравнение называется обыкновенным дифференциальным уравнением (см. (7.1) и (7.2)).
Определение 7.3. Если неизвестная функция в дифференциальном уравнении зависит от двух и более независимых переменных, то такое уравнение называется дифференциальным уравнением в частных производных (см. (7.3)).
Отметим, что далее мы будем изучать методы решения обыкновенных дифференциальных уравнений.
Определение 7.4. Наивысший порядок производной или дифференциала неизвестной функции в обыкновенном дифференциальном уравнении показывает его порядок.
Например, 
есть обыкновенное дифференциальное уравнение первого порядка, так как наивысший порядок производной неизвестной функции 
первый, 
обыкновенное дифференциальное уравнение второго порядка, 
обыкновенное дифференциальное уравнение второго порядка.
Ниже приведем определения общего, частного и особого решений дифференциального уравнения на примере дифференциального уравнения первого порядка вида
(7.4)
Определение 7.5. Функция 
называется общим решением дифференциального уравнения (7.4), если:
1. уравнение разрешимо относительно произвольной постоянной 
то есть 
(
может стремится и к бесконечности).
2. функция удовлетворяет дифференциальному уравнению (7.4) при всех частных значениях произвольной постоянной 
, определяемых формулой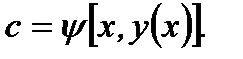 
Отметим, что в общем решении любого дифференциального уравнения постоянная не всегда должна принимать произвольные значения, так как она определяется формулой 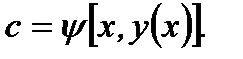Например, если 
для всех допустимых значений 
и 
положительна, то может принимать только положительные произвольные значения.
Как видно будет из дальнейшего изложения материала, решение дифференциального уравнения фактически сводится к вычислению интегралов. Поэтому, иногда говорим не решить дифференциальное уравнение, а интегрировать дифференциальное уравнение. При этом общее решение дифференциального уравнения называется общим интегралом.
Определение 7.6. Решение, полученное из общего решения дифференциального уравнения (7.4) с помощью начального условия Коши 
называется частным решением дифференциального уравнения.
Пример 7.4. Дифференциальное уравнение 
имеет общее решение вида 
где произвольная положительная постоянная. Семейство интегральных кривых – это семейство окружностей с центрами в начале координат (рис. 7.1). Окружность, уравнение которой имеет вид 
есть частное решение дифференциального уравнения. Это решение удовлетворяет начальному условию Коши 
(рис. 7.1).
Определение 7.7. Если дифференциальное уравнение имеет решение, которое не получается из общего решения ни при каком значении 
то такое решение называется особым решением дифференциального уравнения.
