Уравнение вида
 (7.9)
(7.9)
называется уравнением с разделяющимися переменными. В этом уравнении легко разделить переменные, если обе части уравнения разделить на  предполагая при этом, что
предполагая при этом, что  Итак имеем
Итак имеем
 (7.10)
(7.10)
Заметим, что деление обеих частей уравнения (7.9) на 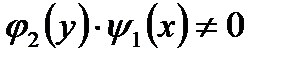 может привести к потере частных решений этого уравнения, обращающих в нуль выражение
может привести к потере частных решений этого уравнения, обращающих в нуль выражение  Поэтому, получив общий интеграл уравнения (7.9), следует проверить, содержит ли он упомянутые частные решения при некоторых значениях
Поэтому, получив общий интеграл уравнения (7.9), следует проверить, содержит ли он упомянутые частные решения при некоторых значениях  Если нет, то эти решения являются особыми решениями исходного дифференциального уравнения. Отметим также, что в процессе разделения переменных в уравнениях с разделяющимися переменными возможно появление и лишних решений, обращающих в нуль множитель
Если нет, то эти решения являются особыми решениями исходного дифференциального уравнения. Отметим также, что в процессе разделения переменных в уравнениях с разделяющимися переменными возможно появление и лишних решений, обращающих в нуль множитель  (в этом случае или
(в этом случае или  или
или  – разрывные функции).
– разрывные функции).
Пример 7.6. Решить уравнение
 (7.11)
(7.11)
Решение. Разделив обе части уравнения на 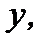 считая, что
считая, что  получим уравнение с разделенными переменными
получим уравнение с разделенными переменными
 (7.12)
(7.12)
Интегрирование последнего приводит к выражению
 (7.13)
(7.13)
где  Потенцируя (7.13), получим
Потенцируя (7.13), получим
 (7.14)
(7.14)
Можно показать, что если теперь  считать произвольной постоянной, включая
считать произвольной постоянной, включая  то знаки модулей слева и справа в (7.14) можно убрать. Итак, общее решение исходного уравнения имеет вид
то знаки модулей слева и справа в (7.14) можно убрать. Итак, общее решение исходного уравнения имеет вид
 (7.15)
(7.15)
где –  произвольная постоянная.
произвольная постоянная.
Заметим, что решение  исходного уравнения получается из полученного общего решения (7.15) при
исходного уравнения получается из полученного общего решения (7.15) при 
Ответ: 
Пример 7.7. Полные издержки  есть функция объема производства
есть функция объема производства  Известно, что предельные издержки равны средним издержкам. Найти закон изменения
Известно, что предельные издержки равны средним издержкам. Найти закон изменения 
Решение. По условию задачи имеем
 (7.16)
(7.16)
Уравнение (7.16) является дифференциальным уравнением первого порядка с разделяющимися переменными. Разделяя переменные в (7.16), получим
 (7.17)
(7.17)
Интегрирование уравнения (7.17) с разделенными переменными приводит к следующему общему решению
 (7.18)
(7.18)
где  (7.18) показывает, что когда предельные издержки равны средним издержкам, то издержки в зависимости от объема производства меняются по линейному закону.
(7.18) показывает, что когда предельные издержки равны средним издержкам, то издержки в зависимости от объема производства меняются по линейному закону.
Ответ: 
Пример 7.8. Решить задачу Коши
 (7.19)
(7.19)
Решение. Уравнение (7.19) является уравнением с разделяющимися переменными. Разделим обе части уравнения на  Врезультате получим уравнение с разделенными переменными
Врезультате получим уравнение с разделенными переменными
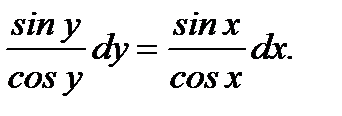 (7.20)
(7.20)
Интегрируя (7.20), получим
 (7.21)
(7.21)
где  произвольная постоянная, не равная нулю. Частное решение получим, пользуясь начальным условием Коши
произвольная постоянная, не равная нулю. Частное решение получим, пользуясь начальным условием Коши  Итак, имеем
Итак, имеем
 (7.22)
(7.22)
Тогда частное решение имеет вид
 (7.23)
(7.23)
Отметим, что к уравнениям с разделяющимися переменными приводятся уравнения вида
 (7.24)
(7.24)
где  действительные постоянные, подстановкой
действительные постоянные, подстановкой
 (7.25)
(7.25)
Пример 7.9. Решить уравнение
 (7.26)
(7.26)
Решение. Введем новую переменную  Тогда
Тогда  и исходное уравнение преобразуется к виду
и исходное уравнение преобразуется к виду
 (7.27)
(7.27)
Интегрируя последнее и переходя к переменной  получим общее решение уравнения (7.26) в виде
получим общее решение уравнения (7.26) в виде
 (7.28)
(7.28)
где  произвольная постоянная.
произвольная постоянная.
Ответ: 
Однородные уравнения.
Однородными дифференциальными уравнениями первого порядка называются уравнения вида
 либо
либо  (7.29)
(7.29)
где  нулевой степени однородная функция относительно
нулевой степени однородная функция относительно  и
и  а
а  и
и  однородные функции относительно
однородные функции относительно  и
и  одинаковой степени. Напомним, что функция двух переменных
одинаковой степени. Напомним, что функция двух переменных  называется однородной функцией степени
называется однородной функцией степени  относительно
относительно  и
и  если для любого действительного числа
если для любого действительного числа  справедливо соотношение
справедливо соотношение
 (7.30)
(7.30)
Например, функция  относительно
относительно  и
и  второй степени однородная функция, так как
второй степени однородная функция, так как

А функция  относительно
относительно  и
и  нулевой степени однородная функция, так как
нулевой степени однородная функция, так как

Однородные уравнения (7.29) приводятся к уравнениям с разделяющимися переменными заменой  с учетом того, что
с учетом того, что 
Пример 7.10. Решить уравнение
 (7.31)
(7.31)
Решение. Разрешив (7.31) относительно производной  и убедившись, что данное уравнение является однородным, делаем замену переменной
и убедившись, что данное уравнение является однородным, делаем замену переменной  . Отсюда
. Отсюда
 (7.32)
(7.32)
Подставляя значения  и
и  из (7.32) в исходное уравнение, его можно преобразовать к уравнению с разделяющимися переменными
из (7.32) в исходное уравнение, его можно преобразовать к уравнению с разделяющимися переменными
 (7.33)
(7.33)
Разделив переменные, считая, что  получим уравнение с разделенными переменными
получим уравнение с разделенными переменными
 (7.34)
(7.34)
Интегрируя (7.34), получим

или
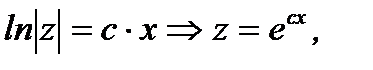 (7.35)
(7.35)
где  произвольная постоянная. Переходя в (7.35) к функции
произвольная постоянная. Переходя в (7.35) к функции  получим общее решение исходного дифференциального уравнения в виде
получим общее решение исходного дифференциального уравнения в виде
 (7.36)
(7.36)
Заметим, что при делении обеих частей уравнения (7.34) на  можно было потерять решение
можно было потерять решение  исходного уравнения (7.31). Из полученного общего решения (7.36) видно, что данное решение получается при значении постоянной
исходного уравнения (7.31). Из полученного общего решения (7.36) видно, что данное решение получается при значении постоянной 
Ответ: 
Пример 7.11. Решить уравнение
 (7.37)
(7.37)
Решение. Здесь  Так как
Так как  являются однородными функциями первой степени относительно
являются однородными функциями первой степени относительно  и
и  , то уравнение (7.37) является однородным уравнением первого порядка. После замены переменной
, то уравнение (7.37) является однородным уравнением первого порядка. После замены переменной  с учетом того, что
с учетом того, что 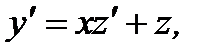 приходим к уравнению с разделяющимися переменными вида
приходим к уравнению с разделяющимися переменными вида
 (7.38)
(7.38)
Разделив переменные в (7.38) и интегрируя, получим общий интеграл уравнения (7.37)
 (7.39)
(7.39)
где  произвольная постоянная.
произвольная постоянная.
Ответ: 
К однородному дифференциальному уравнению первого порядка приводятся уравнения вида
 (7.40)
(7.40)
где  действительные постоянные.
действительные постоянные.
Если прямые  и
и  пересекаются в точке с координатами
пересекаются в точке с координатами 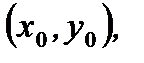 то введением новых переменных
то введением новых переменных  и
и  формулами
формулами
 (7.41)
(7.41)
уравнение (7.40) приводится к однородному уравнению. Если же прямые параллельны, то подстановка  приводит к уравнению с разделяющимися переменными.
приводит к уравнению с разделяющимися переменными.
Пример 7.12. Решить уравнение
 (7.42)
(7.42)
Решение. Поскольку  то прямые
то прямые  и
и  пересекаются. Решая систему линейных уравнений с двумя неизвестными
пересекаются. Решая систему линейных уравнений с двумя неизвестными
 (7.43)
(7.43)
находим координаты точки пересечения прямых в виде  После введения новых переменных
После введения новых переменных  с учетом того, что
с учетом того, что
 (7.44)
(7.44)
исходное уравнение (7.42) преобразуется к виду
 (7.45)
(7.45)
Последнее уравнение представляет собой однородное уравнение, которое подстановкой  сводится к уравнению с разделяющимися переменными вида
сводится к уравнению с разделяющимися переменными вида
 (7.46)
(7.46)
После интегрирования (7.46) получим
 (7.47)
(7.47)
где  произвольная постоянная. Переходя в (7.47) к переменным
произвольная постоянная. Переходя в (7.47) к переменным  и
и  , получим общее решение исходного уравнения
, получим общее решение исходного уравнения
 (7.48)
(7.48)
Ответ: 






