Исследование функции с помощью дифференциального исчисления дает возможность построить график функции по его характерным особенностям. Ниже это покажем на примере.
Пусть дана функция
(3.36)
Требуется исследовать ее с помощью дифференциального исчисления и построить ее график. Для этого надо поступить следующим образом:
1. Найти область определения функции.
Очевидно, что заданная функция определена для 
2. Найти поведение функции вокруг точки 
Имеем 
Отсюда следует, что точка 
является точкой разрыва второго рода или точкой бесконечного разрыва.
3. Найти точки пересечения графика с осями координат.
и 
То есть, график пересекает ось 
в точках с координатами 
и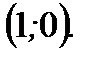 
4. Исследовать функцию на четность и нечетность.
Если 
то функция четная и ее график симметричен относительно оси ординат (например, 
четная). Если 
то функция нечетная и ее график симметричен относительно начала координат (например, 
нечетная).Так как заданная функция не удовлетворяет условиям четности и нечетности, то она не обладает четностью.
5. Исследовать функцию на периодичность.
Если 
то функция периодическая с периодом 
Так как заданная функция не удовлетворяет условию периодичности, то она не периодическая.
6. Найти экстремумы (максимумы и минимумы) функции.
Для нахождения точек возможного экстремума пользуемся необходимым условием экстремума дифференцируемой функции (если дифференцируемая функция 
имеет maxили min, то в точках максимума или минимума 
). Итак, имеем
Каждую точку возможного экстремума должны исследовать на максимум или минимум с помощью достаточных условий. Первое достаточное условие связано со знаком первого порядка производной заданной функции вокруг точки возможного экстремума, а именно если 
и 
, то в данной точке функция имеет min, а если 
и 
, то в данной точке функция имеет max (см. рисунок 3.10).
Второе достаточное условие связано со знаком второго порядка производной заданной функции в экстремальной точке, а именно, если 
, то в данной точке функция имеет min, а если 
, то в данной точке функция имеет max (см. рисунок 3.10).
Вычислим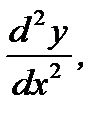 
учитывая выражение для производной первого порядка (см. выше). Итак,
Тогда
Согласно второму достаточному условию экстремума функции имеем:
точка 
есть точка максимума и 
точка 
есть точка минимума и 
точка 
есть точка максимума и 
(см. рисунок 3.11).
7. Найти точки перегиба графика функции.
Для нахождения точек перегиба воспользуемся необходимым условием перегиба (если функция в каких-то точках имеет перегиб, то в этих точках 
). Полученные точки возможного перегиба после решения уравнения нужно исследовать на перегиб с помощью достаточного условия (если 
, а 
или 
, а т 
), то точка 
точно есть точка перегиба.
Приравнивая к нулю второго порядка производную, получим:
(3.37)
(3.37) показывает, что при переходе через точку возможного перегиба второго порядка производная функции меняет знак, то есть график функции меняет направление выпуклости (
направление выпуклости вверх, 
направление выпуклости вниз) (см. рисунок 3.11). Итак, приходим к выводу, что точка 
является точкой перегиба и 
8. Асимптоты.
Если 
или 
, то прямая 
называется вертикальной асимптотой кривой. Если 
или 
, то прямая 
называется горизонтальной асимптотой кривой. Прямая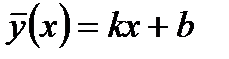 
является наклонной асимптотой кривой, если существуют конечные пределы
(3.38)
или
(3.39)
Заметим, что согласно пункту 2 (см. 3.3.3) прямая 
является вертикальной асимптотой кривой. Для нахождения наклонной асимптоты вычислим следующие пределы
(3.40)
Рис. 3.11
(3.41)
Как следует из (3.40) и (3.41), прямая 
является наклонной асимптотой кривой. Итак, согласно проведенному исследованию можно построить график заданной функции (см. рис. 3.11).
