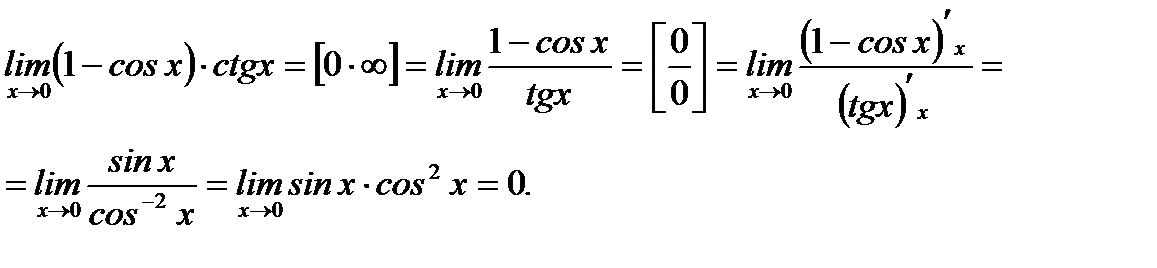Пример 3.28. Найти производную функции 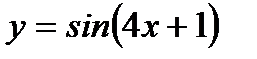 по
по 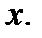
Решение. Согласно (3.23) и правилам вычисления производных от элементарных функций имеем
 Ответ:
Ответ: 
Пример 3.29. Найти производную функции 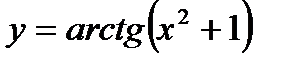 по
по 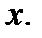
Решение. Согласно (3.23) и правилам вычисления производных от элементарных функций имеем
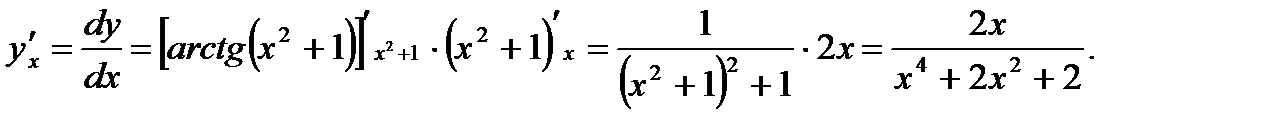
Ответ: 
Пример 3.30. Найти производную функции 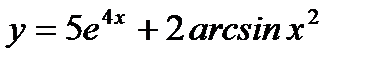 по
по 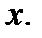
Решение. Согласно (3.23) и правилам вычисления производных от элементарных функций имеем
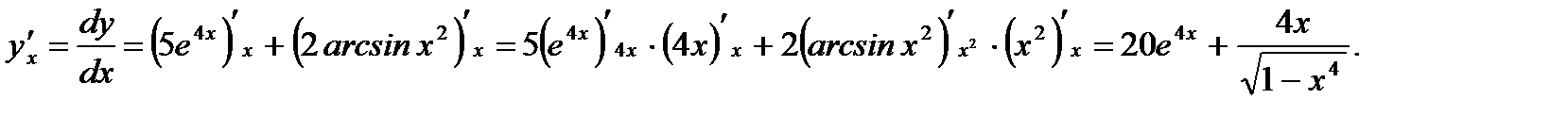
Ответ: 
Пример 3.31. Найти производную функции  по
по 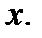
Решение. Согласно (3.23) и правилам вычисления производных от элементарных функций имеем
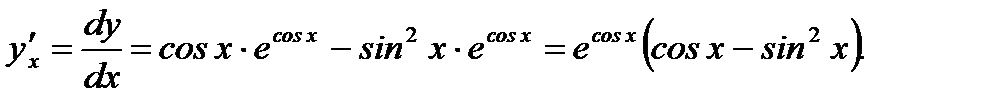
Ответ: 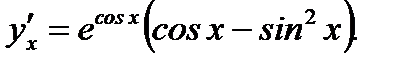
Пример 3.32. Найти производную функции  по
по 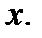
Решение. Согласно (3.23) и правилам вычисления производных от элементарных функций имеем
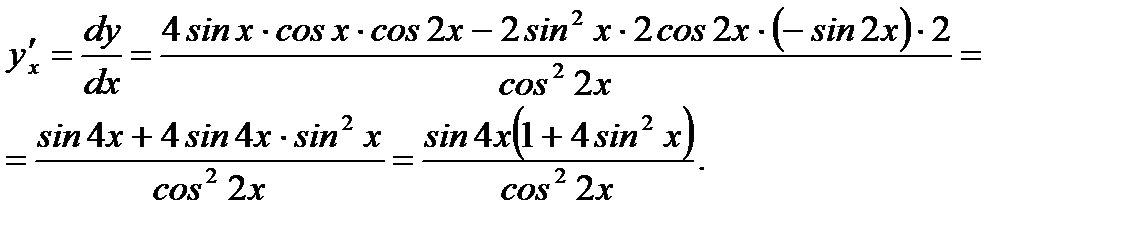
Ответ: 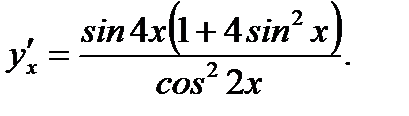
Пример 3.33. Найти производную функции  по
по 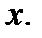
Решение. Согласно (3.23) и правилам вычисления производных от элементарных функций имеем

Ответ: 
Пример 3.34. Найти производную функции 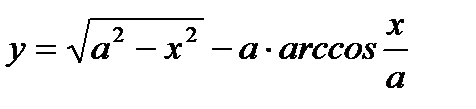 по
по 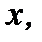 где
где 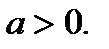
Решение. Согласно (3.23) и правилам вычисления производных от элементарных функций имеем
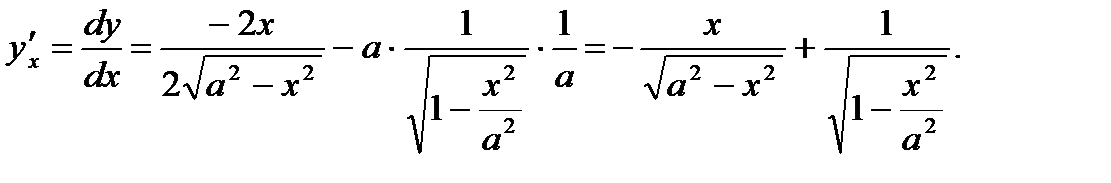
Ответ: 
Пример 3.35. Найти производную функции  по
по 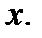
Решение. Согласно (3.28) и правилам вычисления производных от элементарных функций имеем

Ответ: 
Пример 3.36. Найти производную функции 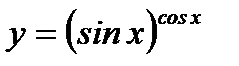 по
по 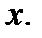
Решение. Согласно (3.28) и правилам вычисления производных от элементарных функций имеем
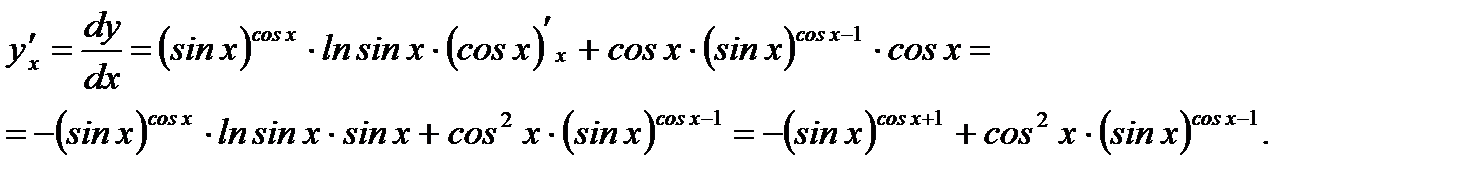
Ответ: 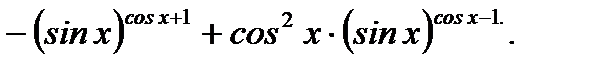
Пример 3.37. Пусть издержки производства 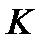 как функция от количества продукции
как функция от количества продукции 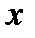 имеют вид
имеют вид  Найти предельные издержки производства при
Найти предельные издержки производства при  и
и  .
.
Решение. По определению предельных издержек производства имеем


Ответ: 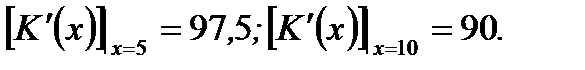
Пример 3.38. Количество 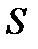 продукции, выпускаемой за время
продукции, выпускаемой за время 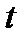 , определяется формулой
, определяется формулой 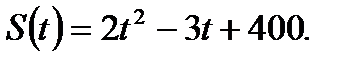 Вычислить производительность
Вычислить производительность 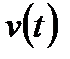 выпуска продукции в моменты времени
выпуска продукции в моменты времени 
Решение. Так как 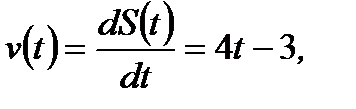 то
то


Ответ: 
Пример 3.39. Функция  задана в параметрическом виде формулами
задана в параметрическом виде формулами 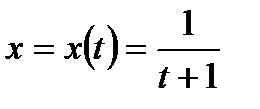 и
и  Найти
Найти 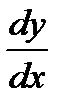 .
.
Решение. Согласно (3.30) имеем

Ответ: 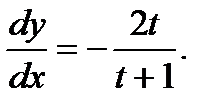
Пример 3.40. Функция  задана в неявном виде формулой
задана в неявном виде формулой  Найти
Найти 
Решение. Дифференцируя обе части уравнения  по
по 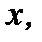 получим:
получим:
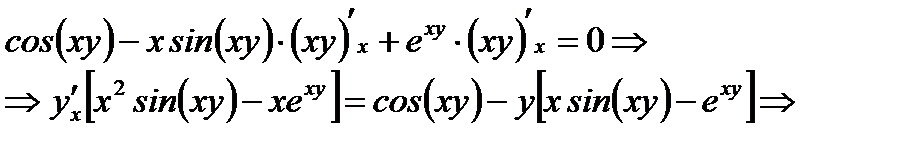
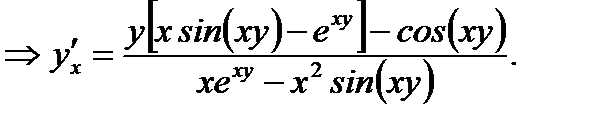
Ответ: 
Пример 3.40. Найти производную 6-го порядка от функции 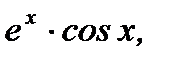 пользуясь формулой Лейбница.
пользуясь формулой Лейбница.
Решение. Согласно (3.33), имеем

Ответ: 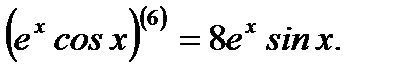
Пример 3.41. Найти производную второго порядка функции 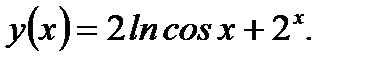
Решение. Имеем

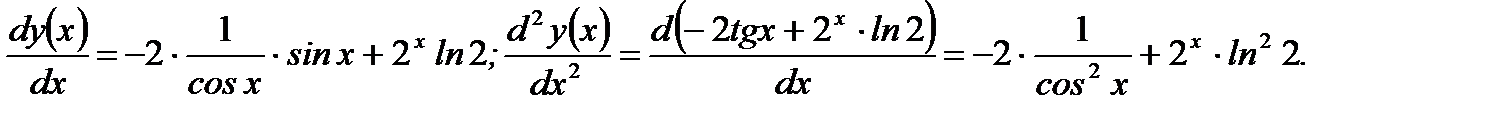
Ответ: 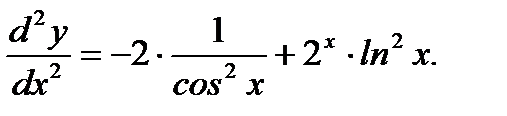
Пример 3.42. Найти дифференциал первого порядка функции 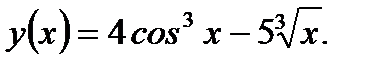
Решение. Согласно определению 3.8 имеем

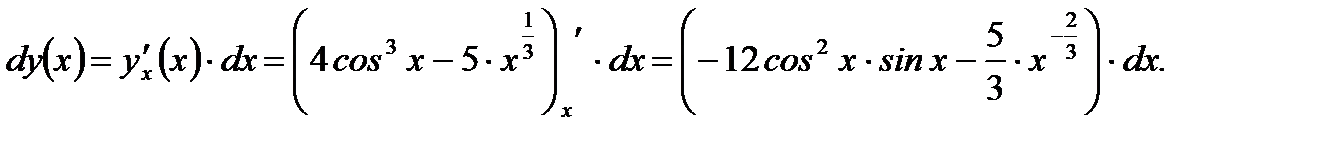
Ответ: 
Пример 3.43. Найти дифференциал второго порядка функции 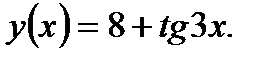
Решение. Согласно (3.29) имеем


Ответ: 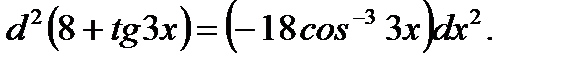
Пример 3.44. Вычислить предел 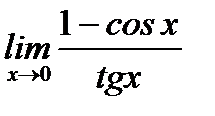 , пользуясь правилами Лопиталя.
, пользуясь правилами Лопиталя.
Решение. 
Ответ: 
Пример 3.45. Вычислить предел 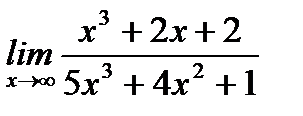 , пользуясь правилами Лопиталя.
, пользуясь правилами Лопиталя.
Решение. 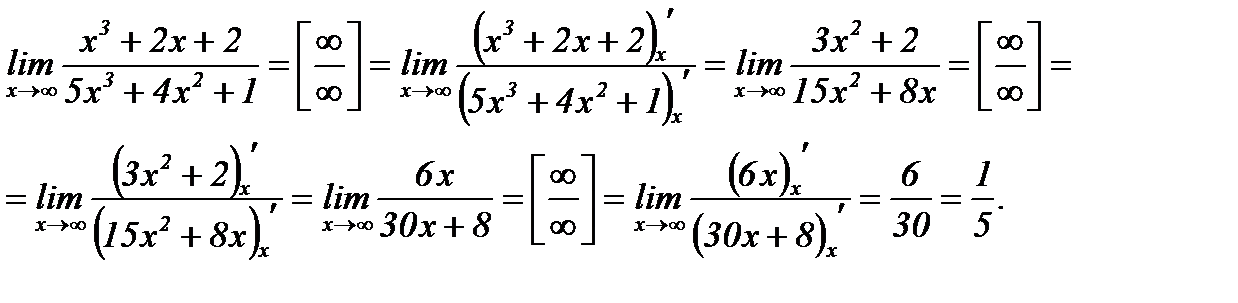
Ответ: 
Пример 3.46. Вычислить предел 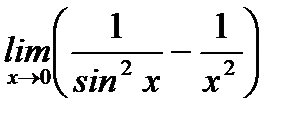 , пользуясь правилами Лопиталя и эквивалентными бесконечно малыми.
, пользуясь правилами Лопиталя и эквивалентными бесконечно малыми.
Решение. 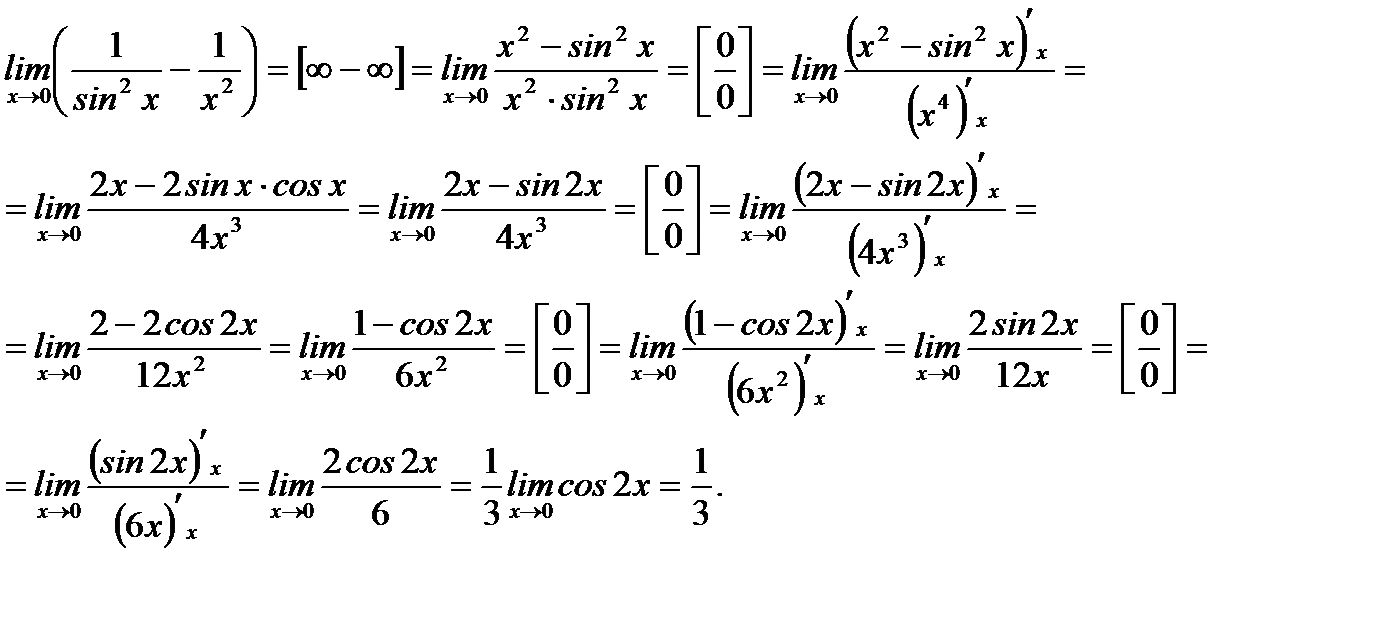
Ответ: 
Пример 3.47. Вычислить предел 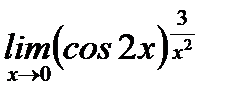 , пользуясь правилами Лопиталя.
, пользуясь правилами Лопиталя.
Решение. 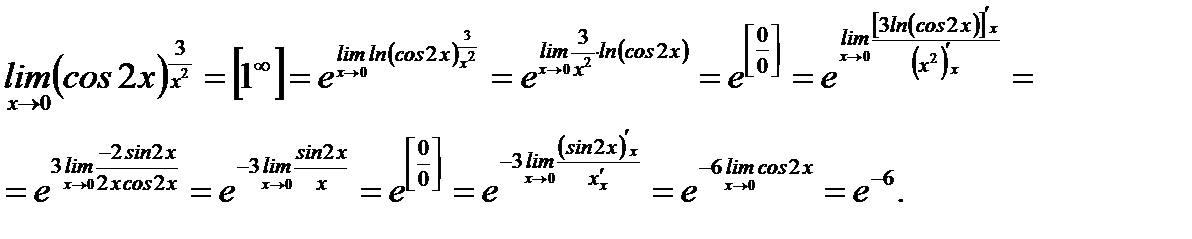
Ответ: 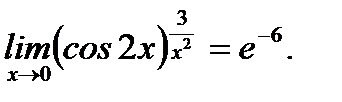
Пример 3.48. Вычислить предел 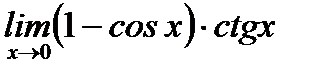 , пользуясь правилами Лопиталя.
, пользуясь правилами Лопиталя.
Решение. 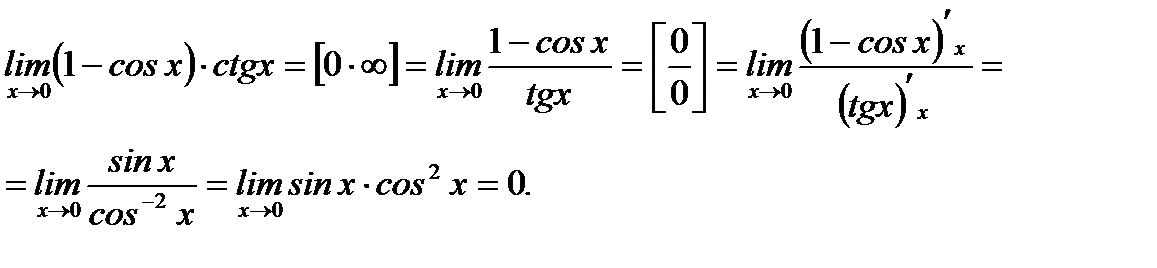
Ответ: 
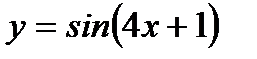 по
по 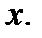
 Ответ:
Ответ: 
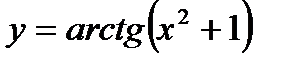 по
по 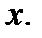
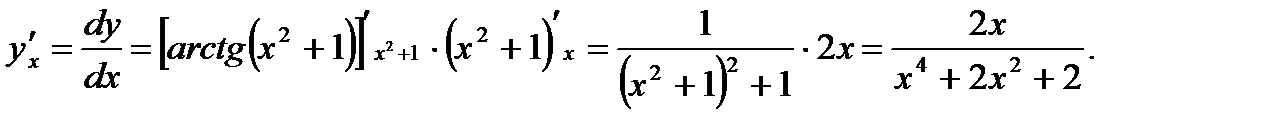

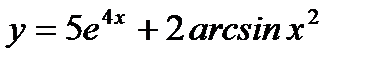 по
по 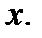
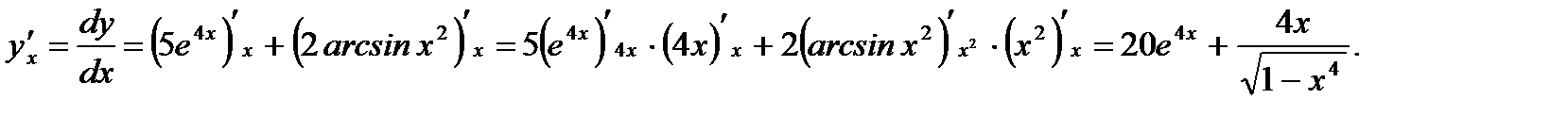

 по
по 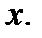
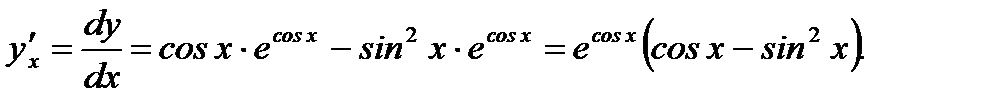
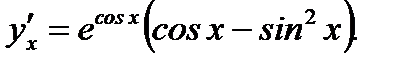
 по
по 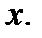
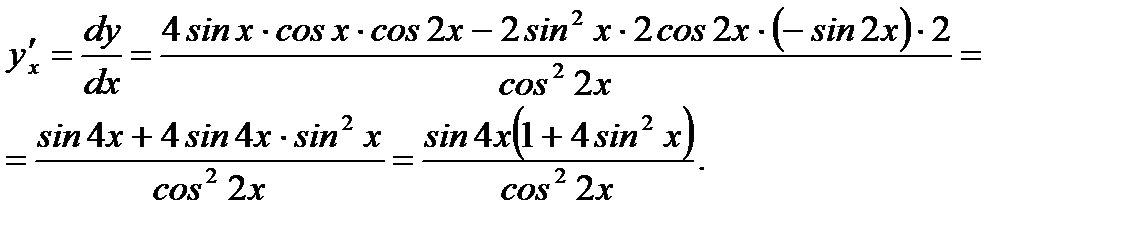
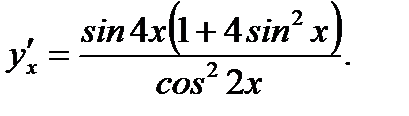
 по
по 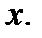


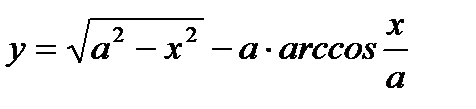 по
по 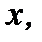 где
где 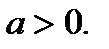
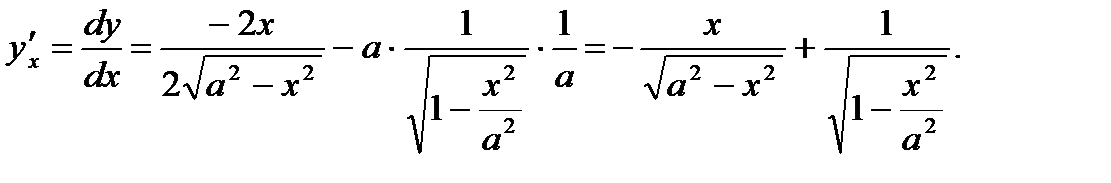

 по
по 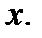


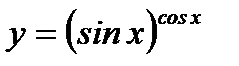 по
по 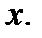
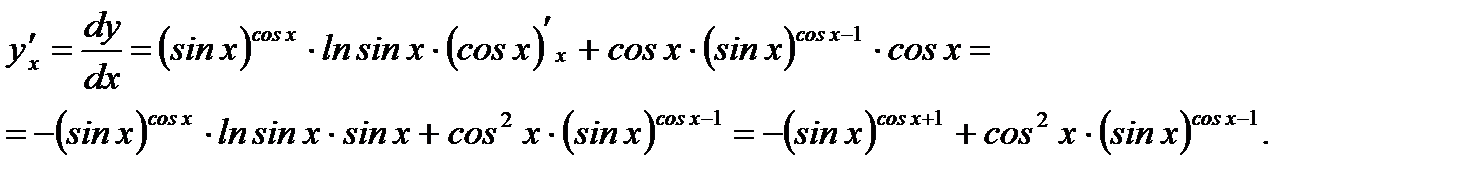
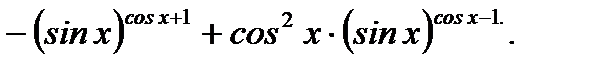
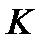 как функция от количества продукции
как функция от количества продукции 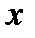 имеют вид
имеют вид  Найти предельные издержки производства при
Найти предельные издержки производства при  и
и  .
.

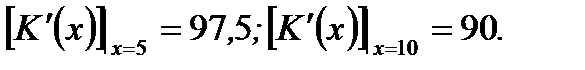
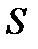 продукции, выпускаемой за время
продукции, выпускаемой за время 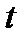 , определяется формулой
, определяется формулой 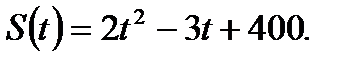 Вычислить производительность
Вычислить производительность 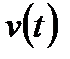 выпуска продукции в моменты времени
выпуска продукции в моменты времени 
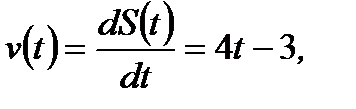 то
то


 задана в параметрическом виде формулами
задана в параметрическом виде формулами 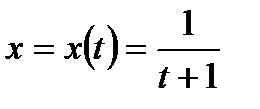 и
и  Найти
Найти 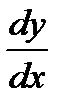 .
.
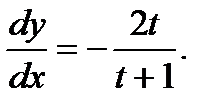
 задана в неявном виде формулой
задана в неявном виде формулой  Найти
Найти 
 по
по 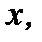 получим:
получим: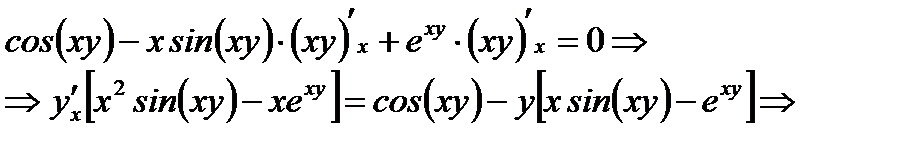
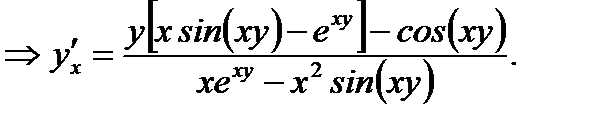

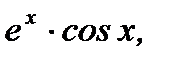 пользуясь формулой Лейбница.
пользуясь формулой Лейбница.
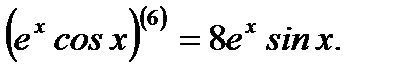
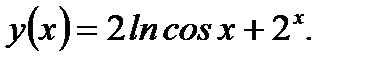

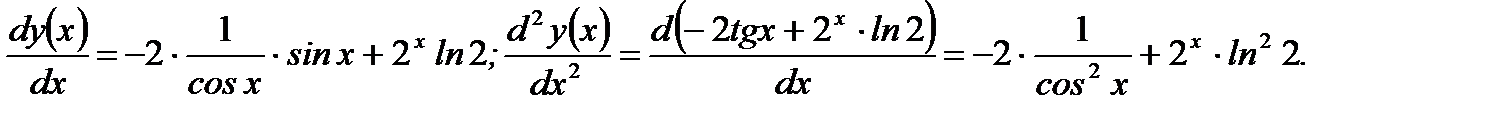
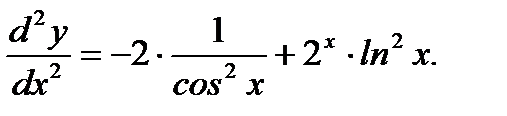
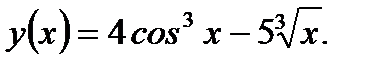

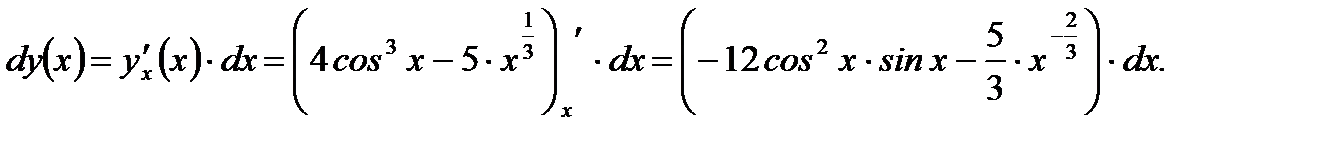

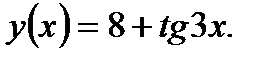


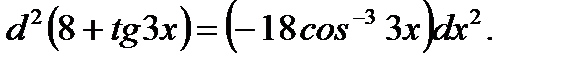
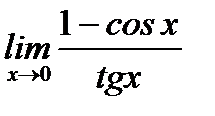 , пользуясь правилами Лопиталя.
, пользуясь правилами Лопиталя.

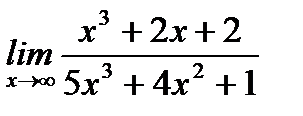 , пользуясь правилами Лопиталя.
, пользуясь правилами Лопиталя.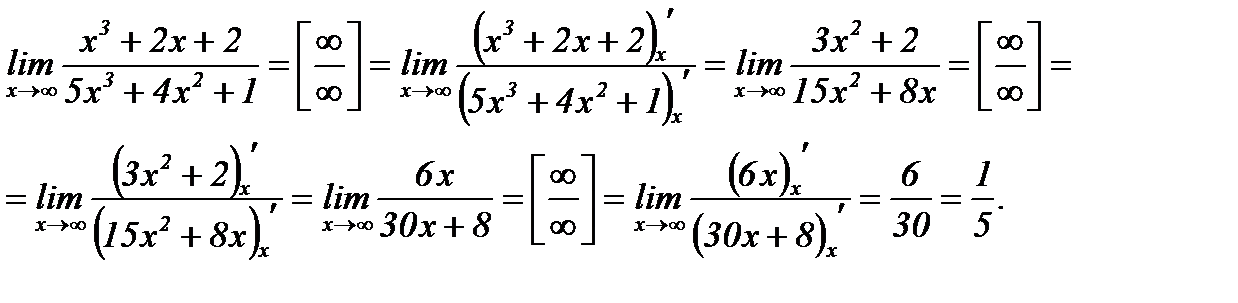

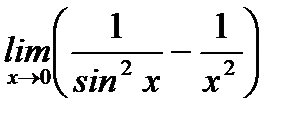 , пользуясь правилами Лопиталя и эквивалентными бесконечно малыми.
, пользуясь правилами Лопиталя и эквивалентными бесконечно малыми.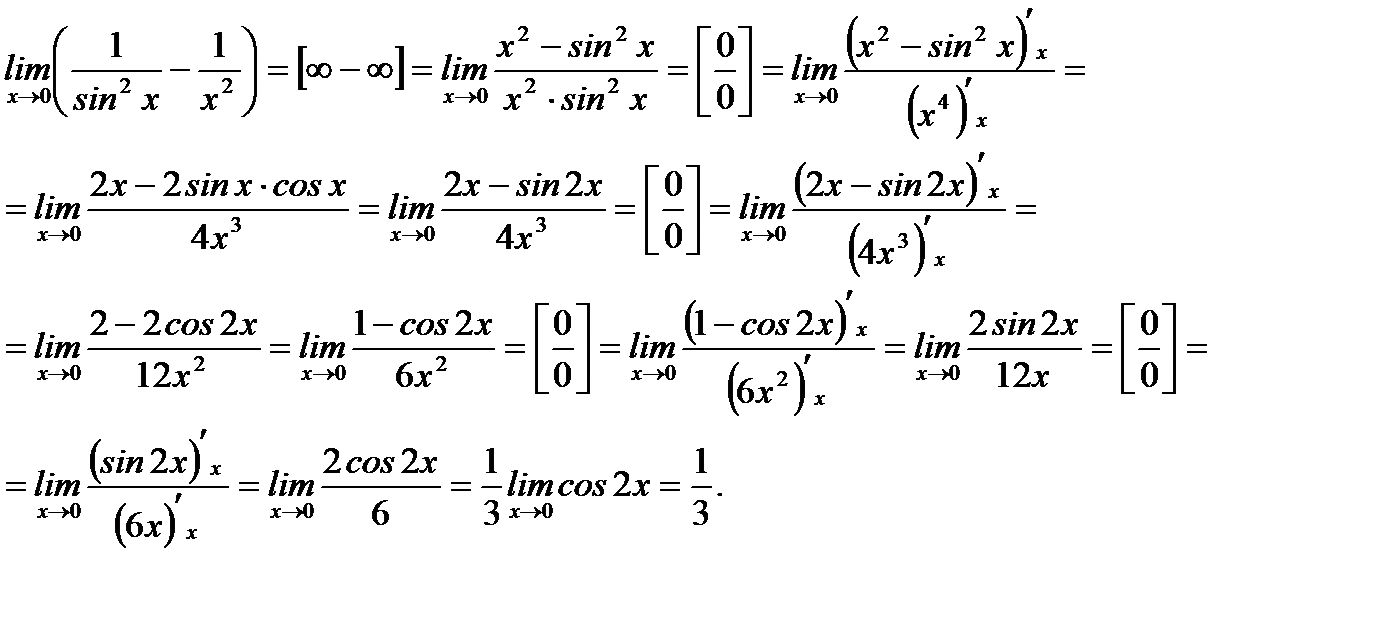

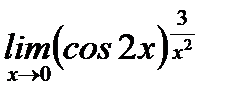 , пользуясь правилами Лопиталя.
, пользуясь правилами Лопиталя.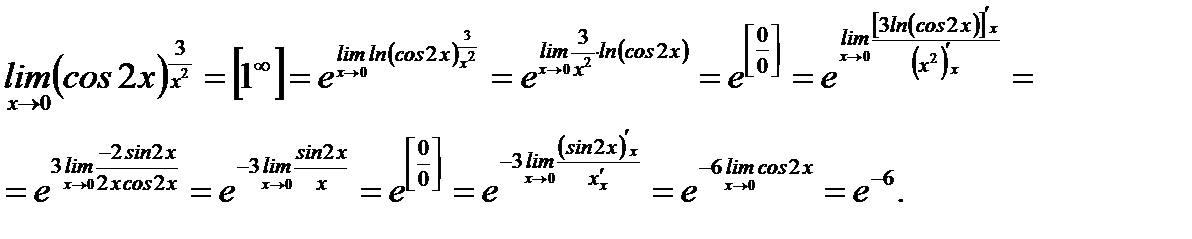
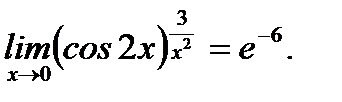
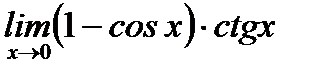 , пользуясь правилами Лопиталя.
, пользуясь правилами Лопиталя.