Различные виды уравнения плоскости в пространстве.
1. Общее уравнение плоскости в пространстве.
Линейная связь между переменными  в трехмерной прямоугольной системе координат вида
в трехмерной прямоугольной системе координат вида
 (2.59)
(2.59)
где  действительные числа, представляет общее уравнение плоскости в пространстве (рис. 2.20). Пусть точка
действительные числа, представляет общее уравнение плоскости в пространстве (рис. 2.20). Пусть точка  принадлежит плоскости
принадлежит плоскости 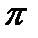 (
( ).
).

Тогда очевидно, что
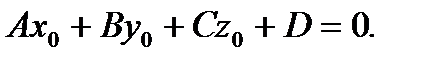
Имеем
 (2.60)
(2.60)
(2.60) есть уравнение плоскости, которая проходит через заданную точку 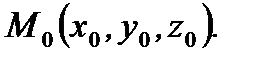 Введем вектор
Введем вектор  . Если учесть еще, что
. Если учесть еще, что  , то из (2.60) можно сделать вывод, что
, то из (2.60) можно сделать вывод, что  То есть, вектор
То есть, вектор  перпендикулярен плоскости
перпендикулярен плоскости  Он называется нормальным вектором плоскости.
Он называется нормальным вектором плоскости.
2. Нормированное уравнение плоскости.
При решении задачи нахождения расстояния заданной точки  от заданной плоскости
от заданной плоскости  нужно пользоваться нормированным уравнением плоскости (рис. 2.21).
нужно пользоваться нормированным уравнением плоскости (рис. 2.21).

Рис. 2.21
Оно имеет вид
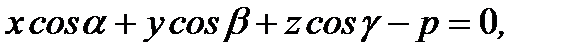 (2.61)
(2.61)
где  - текущие координаты точки
- текущие координаты точки 
 есть углы между единичным вектором
есть углы между единичным вектором 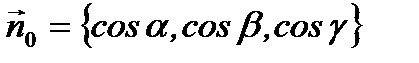 нормального вектора
нормального вектора  плоскости и осями
плоскости и осями  , соответственно,
, соответственно,  (рис. 2.21). Общее уравнение плоскости приводится к нормированному виду таким же способом, как и в случае прямой на плоскости. При этом нормирующий множитель имеет вид
(рис. 2.21). Общее уравнение плоскости приводится к нормированному виду таким же способом, как и в случае прямой на плоскости. При этом нормирующий множитель имеет вид

 (2.62)
(2.62)
Причем при  берем
берем  если
если  и
и 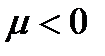 если
если  Тогда отклонение
Тогда отклонение  точки
точки  от плоскости
от плоскости  выражается формулой
выражается формулой
 (2.63)
(2.63)
aрасстояние 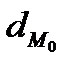 точки
точки  от плоскости
от плоскости  есть
есть 
Пример 2.15. Найти расстояние  точки
точки  от плоскости
от плоскости 
Решение. Так как свободный член в общем уравнении плоскости имеет отрицательный знак при положительном знаке коэффициента при  , то нормирующий множитель имеет вид
, то нормирующий множитель имеет вид
 (2.64)
(2.64)
Умножая обе части общего уравнения плоскости на  , получим нормированное уравнение плоскости в виде
, получим нормированное уравнение плоскости в виде
 (2.65)
(2.65)
Тогда согласно (2.63) имеем
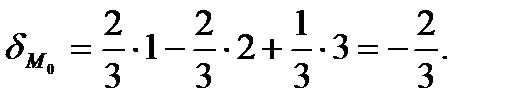
Для расстояния точки  от данной плоскости получим
от данной плоскости получим

Ответ: 
Пример 2.16. Составить уравнение плоскости, проходящей через точки  (рис. 2.22).
(рис. 2.22).
Решение. На заданной плоскости возьмем точку  с текущими координатами
с текущими координатами 
 Из условий задачи следует, что
Из условий задачи следует, что 
 Так как эти три векторы лежат на одной плоскости, то они компланарны. Тогда согласно теореме 2.3 их смешанное произведение равно нулю, то есть
Так как эти три векторы лежат на одной плоскости, то они компланарны. Тогда согласно теореме 2.3 их смешанное произведение равно нулю, то есть
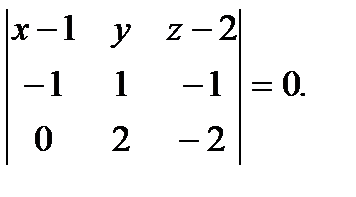
 (2.66)
(2.66)
Раскрывая определитель по элементам первой строки, получим


Ответ:  Плоскость параллельна оси
Плоскость параллельна оси 

Пример 2.17. (задача экономического характера) Себестоимость  какого-то одного изделия складывается из постоянных расходов, равных 150 рублям и затрат золота и серебра, цена которых 400 рублей и 200 рублей за грамм. Найти зависимость себестоимости от количества золота и серебра
какого-то одного изделия складывается из постоянных расходов, равных 150 рублям и затрат золота и серебра, цена которых 400 рублей и 200 рублей за грамм. Найти зависимость себестоимости от количества золота и серебра  и
и  (в граммах), затраченного на одно изделие.
(в граммах), затраченного на одно изделие.
Решение. Из условий задачи ясно, что на  грамм золота затрачивается
грамм золота затрачивается  рублей, а на
рублей, а на  грамм серебра –
грамм серебра –  рублей. То есть,
рублей. То есть, 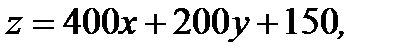 что фактически представляет общее уравнение плоскости в пространстве.
что фактически представляет общее уравнение плоскости в пространстве.
Ответ: 






