Раздел II
Аналитическая геометрия
Векторная алгебра.
Определители и правила Крамера.
Таблица из четырех чисел  , равная числу
, равная числу  называется определителем второго порядка. При этом
называется определителем второго порядка. При этом  являются элементами первой строки,
являются элементами первой строки,  элементами второй строки,
элементами второй строки,  являются элементами первого столбца,
являются элементами первого столбца,  элементами второго столбца. Итак, имеем
элементами второго столбца. Итак, имеем
 (2.1)
(2.1)
Таблица из девяти чисел  , равная числу
, равная числу  называется определителем третьего порядка. Чтобы раскрыть определитель третьего порядка и получить число
называется определителем третьего порядка. Чтобы раскрыть определитель третьего порядка и получить число  пользуемся правилом, согласно которому определитель третьего порядка можно раскрыть по элементам любой строки или любого столбца. Для примера покажем, как раскрыть определитель третьего порядка по элементам первой строки. Берем первый элемент первой строки
пользуемся правилом, согласно которому определитель третьего порядка можно раскрыть по элементам любой строки или любого столбца. Для примера покажем, как раскрыть определитель третьего порядка по элементам первой строки. Берем первый элемент первой строки  умножаем на
умножаем на 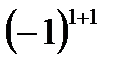 (в показателе числа
(в показателе числа  стоит сумма номеров строки и столбца на пересечении которых находится элемент
стоит сумма номеров строки и столбца на пересечении которых находится элемент  ) и результат умножаем на определитель второго порядка, который получается мысленным вычеркиванием первой строки и первого столбца. Далее поступаем аналогичным образом и с остальными элементами первой строки
) и результат умножаем на определитель второго порядка, который получается мысленным вычеркиванием первой строки и первого столбца. Далее поступаем аналогичным образом и с остальными элементами первой строки  и
и 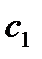 ,и суммируем все полученные числа. Таким образом, имеем
,и суммируем все полученные числа. Таким образом, имеем
 (2.2)
(2.2)
Ниже приведем некоторые из основных свойств определителей:
1. При замене строк столбцами величина определителя не меняется, т.е.
 (2.3)
(2.3)
2. При замене элементов двух строк или двух столбцов местами перед определителем появляется знак минус, т.е.
 (2.4)
(2.4)
3. Если элементы какой-то строки или какого-то столбца равны нулю, то определитель равен нулю, т.е.
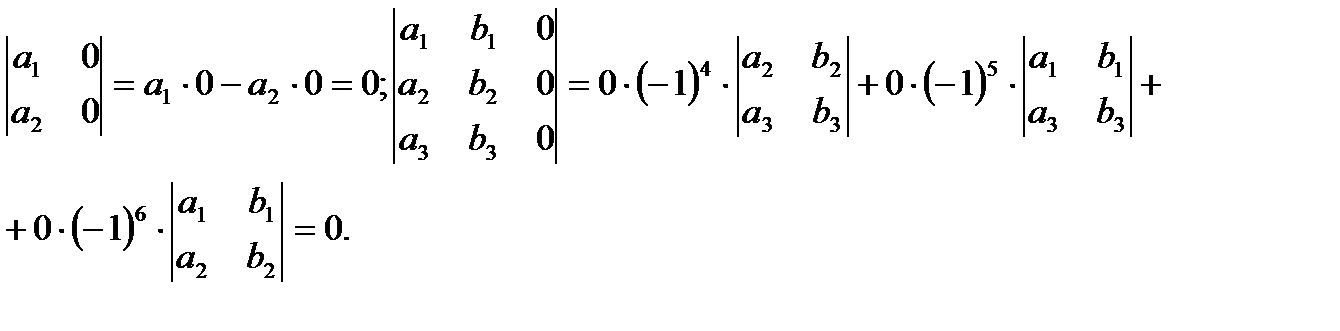
Рассмотрим линейную неоднородную систему с двумя неизвестными  ,
,  и с постоянными действительными коэффициентами
и с постоянными действительными коэффициентами
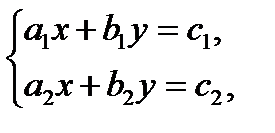 (2.5)
(2.5)
где  и
и  одновременно, или
одновременно, или  или
или 
Если систему (2.5) решить известным методом исключения, то получим
 (2.6)
(2.6)
где  Легко заметить, что числители и знаменатели у
Легко заметить, что числители и знаменатели у  и
и  можно представить с помощью определителей второго порядка в виде
можно представить с помощью определителей второго порядка в виде
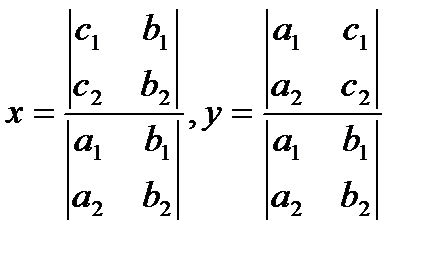 . (2.7)
. (2.7)
Обозначая, как обычно принято,  (основной определитель системы),
(основной определитель системы),  из (2.7) получим
из (2.7) получим
 (2.8)
(2.8)
Правила (2.8), с помощью которых можно найти решение системы (2.5), называются правилами Крамера.
Для линейной неоднородной системы с тремя неизвестными
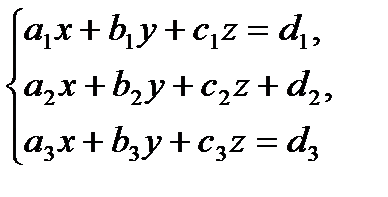 (2.9)
(2.9)
правила Крамера имеют вид
 ,
, 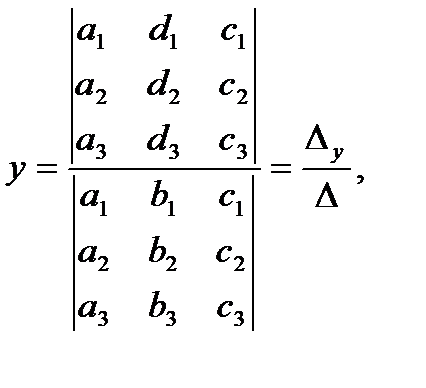
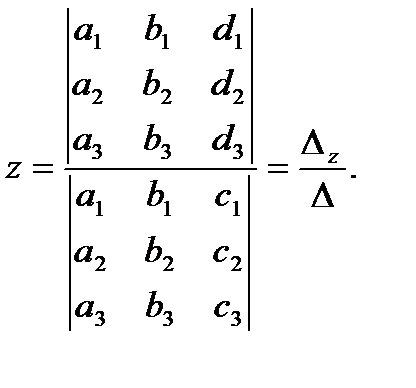 (2.10)
(2.10)
Пример 2.1. Найти решение системы по правилам Крамера

Решение. Согласно (2.8) имеем

Ответ: 
Пример 2.2. Найти решение системы по правилам Крамера

Решение. Вычислим определители 




Далее согласно (2.10) имеем

Ответ: 
Основные понятия и определения векторной алгебры.
Как известно, масса тела  , плотность вещества
, плотность вещества  , объем пространственных тел
, объем пространственных тел  площадь плоских фигур
площадь плоских фигур  и так далее не имеют направления. Такие величины называются скалярными. А такие величины, как сила
и так далее не имеют направления. Такие величины называются скалярными. А такие величины, как сила 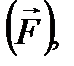 действующая на тело, скорость движения
действующая на тело, скорость движения  ускорение движения
ускорение движения  вес тела
вес тела 
 и так далее, которые обладают и направлением, называются векторными величинами. В математике векторную величину отмечают стрелкой, указывая её начало и конец. Вектор обозначают или одной буквой
и так далее, которые обладают и направлением, называются векторными величинами. В математике векторную величину отмечают стрелкой, указывая её начало и конец. Вектор обозначают или одной буквой 
или двумя буквами  . При этом
. При этом  указывает начало вектора, а
указывает начало вектора, а 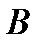 указывает конец вектора (рис. 2.1). Длина стрелки показывает величину (модуль) вектора, а стрелка показывает направление вектора. Если два вектора
указывает конец вектора (рис. 2.1). Длина стрелки показывает величину (модуль) вектора, а стрелка показывает направление вектора. Если два вектора  и
и  исходят из разных начал, то один из векторов можно параллельно себя перенести так, чтобы его начало совпало с началом другого вектора.
исходят из разных начал, то один из векторов можно параллельно себя перенести так, чтобы его начало совпало с началом другого вектора.
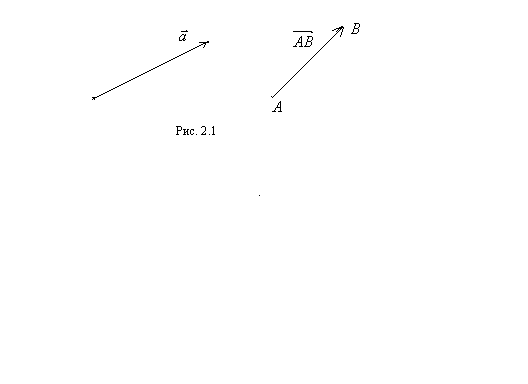
То есть, всегда можно рассматривать двух векторов, исходящих из одного начала. (рис. 2.2).
При умножении вектора на число  получаем вектор, у которого модуль
получаем вектор, у которого модуль  раз больше модуля исходного вектора, а направление совпадает с направлением исходного вектора при
раз больше модуля исходного вектора, а направление совпадает с направлением исходного вектора при  и противоположно направлению исходного вектора при
и противоположно направлению исходного вектора при  При умножении вектора на число
При умножении вектора на число  получаем вектор, у которого модуль
получаем вектор, у которого модуль  раз меньше модуля исходного вектора, а направление совпадает с направлением исходного вектора при
раз меньше модуля исходного вектора, а направление совпадает с направлением исходного вектора при  и противоположно направлению исходного вектора при
и противоположно направлению исходного вектора при 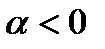 (рис. 2.3).
(рис. 2.3).

Угол 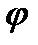 между векторами
между векторами  и
и  считается угол, который меняется в пределах от
считается угол, который меняется в пределах от  до
до 
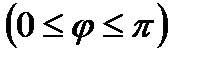 (рис. 2.4). У нулевого вектора
(рис. 2.4). У нулевого вектора 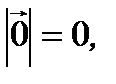 а направление произвольное (рис. 2.4).
а направление произвольное (рис. 2.4).

Действия над векторами.
Сумма и разность векторов. Представление вектора в координатах.
Если два вектора  и
и 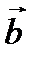 исходят из одного начала, то сумма этих векторов
исходят из одного начала, то сумма этих векторов 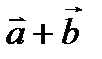 есть вектор, который получается, когда вектор
есть вектор, который получается, когда вектор  параллельно себя переносим так, чтобы его начало совпало с концом вектора
параллельно себя переносим так, чтобы его начало совпало с концом вектора  и соединяем начало вектора
и соединяем начало вектора  с концом вектора
с концом вектора  после параллельного переноса (рис. 2.5).
после параллельного переноса (рис. 2.5).
Если два вектора  и
и 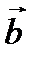 исходят из одного начала, то разность этих векторов
исходят из одного начала, то разность этих векторов  есть вектор, исходящий с конца вектора
есть вектор, исходящий с конца вектора  к концу вектора
к концу вектора  (рис. 2.5).
(рис. 2.5).
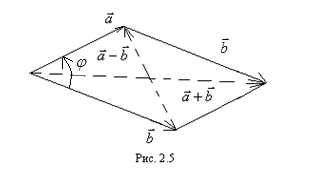
Отметим, что, как видно из рисунка 2.5, сумма векторов  по модулю равна длине большей диагонали, а разность векторов
по модулю равна длине большей диагонали, а разность векторов 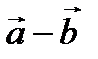 по модулю равна длине меньшей диагонали параллелограмма, построенного на этих векторах
по модулю равна длине меньшей диагонали параллелограмма, построенного на этих векторах 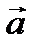 и
и  , как на сторонах.
, как на сторонах.
Пример 2.3. Найти  и
и  , если известно, что
, если известно, что  и угол между ними
и угол между ними 
Решение. По теореме косинусов имеем


Тогда
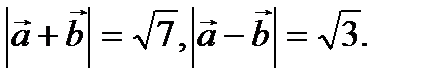
Ответ:
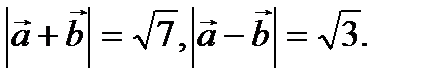
Вектор в двумерной и трехмерной прямоугольной системе координат можно представить в виде разложения по его координатам. Как известно, единичными векторами осей  и
и  в двумерной системе координат являются векторы
в двумерной системе координат являются векторы 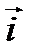 и
и 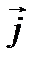 , aединичными векторами осей
, aединичными векторами осей  и
и  в трехмерной системе координат являются векторы
в трехмерной системе координат являются векторы  и
и 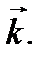 Модули единичных векторов равны единице
Модули единичных векторов равны единице  а их направления совпадают с положительными направлениями осей
а их направления совпадают с положительными направлениями осей  и
и  , соответственно. Эти единичные векторы составляют базис в прямоугольной системе координат. Рассмотрим вектор
, соответственно. Эти единичные векторы составляют базис в прямоугольной системе координат. Рассмотрим вектор 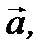 исходящий из начала координат (рис. 2.6). С конца вектора
исходящий из начала координат (рис. 2.6). С конца вектора 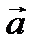 (точка
(точка  ) проведем перпендикуляры к осям
) проведем перпендикуляры к осям  и
и  . Направленный отрезок
. Направленный отрезок  называется иксовой координатой вектора
называется иксовой координатой вектора 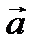 и обозначается через
и обозначается через  а направленный отрезок
а направленный отрезок  называется игрековой координатой вектора
называется игрековой координатой вектора 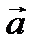 и обозначается через
и обозначается через  Очевидно, что
Очевидно, что  а
а 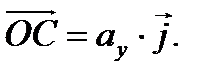 Но по правилам суммы векторов имеем
Но по правилам суммы векторов имеем 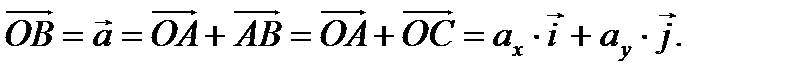 Итак, если
Итак, если 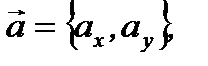 то разложение вектора
то разложение вектора 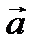 по его координатам имеет вид (рис. 2.6)
по его координатам имеет вид (рис. 2.6)
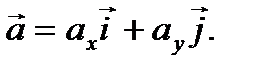 (2.11)
(2.11)
Аналогично, в трехмерной прямоугольной системе координат имеет место разложение вектора  по его координатам
по его координатам 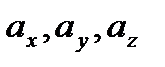 в виде (рис. 2.6)
в виде (рис. 2.6)
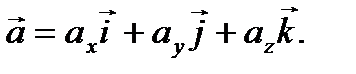 (2.12)
(2.12)

Отметим также, что на основе теоремы Пифагора можно модуль вектора выразить через его координаты следующим образом
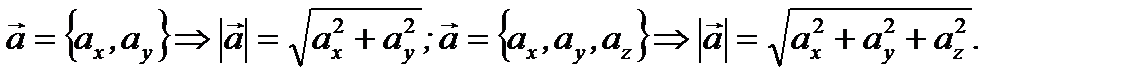
Пример 2.4. Дан вектор  . Разложить его по базису
. Разложить его по базису 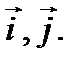
Решение. Согласно (2.11) имеем 
Ответ: 






