Исп. (решает задачу «6 спичек» в плоскости, проходит три минуты).
Эксп. Ваше время уже истекло. Я дам вам еще одну задачу (предлагает задачу «Коробки»).
Исп. (через пять минут решает задачу «Коробки»).
Эксп. Правильно. Может быть, Вы все-таки попробуете решить и первую задачу?
Исп. Опять с какой-нибудь каверзой? (Берется за спички и начинает снова раскладывать их на столе.)
Эксп. (почти тут же). Покажите, пожалуйста, решение второй задачи.
Исп. (ставит коробки).
Эксп. Хорошо. Продолжайте решать задачу со спичками.
Исп. (возвращается к первой задаче, решает ее в плоскости). Не выходит. Тут на плоскости их не разложишь.
Эксп. Поставьте, пожалуйста, еще раз коробки.
Исп. (ставит).
Эксп. Ну, а как все-таки со спичками?
Исп. (решает по-старому). Отказываюсь я ее решать. Ничего не получится. Если я сразу не ухватил идею, то у меня сразу торможение после двух-трех» вариантов получается... А если по полспички взять? > Эксп. Поставьте, пожалуйста, коробки.
Исп. (ставит).
Эксп. А как с первой задачей?
Исп. Отказываюсь, я все равно ее не решу.
Итак, испытуемый уже отдает себе отчет в том, что применявшийся им способ не пригоден («тут на плоскости их не разложишь»)...отказывается от него, после отказа продолжает поиски («а если по полспички взять?») — и все-таки наведение, воспроизводимое им же самим несколько раз, не действует. Значит, все дело в том, что данный способ действия — выход из горизонтальной плоскости в вертикальную — «примелькался» испытуемому, оказался зазубренным, утратил свою новизну. Вследствие этого он не мог вызвать на себя ориентировочную реакцию и повлиять на решение задачи.
До сих пор в описанных опытах в качестве наведения применялась задача, имеющая с основной задачей общий принцип решения. Был поставлен вопрос: а если наведение будет содержать готовый ответ на основную задачу, повлияет ли он на ее решение? Для ответа на этот вопрос необходимо было найти задачу, в результате решения которой испытуемый получал фигуру, составляющую решение задачи «6 спичек», и в то же время, чтобы принцип ее решения был совершенно иной, чем задачи «6 спичек».
Задача «Пробка» удовлетворяла этим условиям.
«В металлической пластинке имеется отверстие в виде правильного треугольника. К нему нужно найти такое объемное тело, чтобы оно любой своей гранью, как пробка, полностью закрывало отверстие и в то же время впритирку проходило через него».
Решив задачу, испытуемый получал в ответе тетраэдр (рис. 5)..-Его просили начертить или вылепить из пластилина эту фигуру. Таким образом, по окончательному ответу задача «6 спичек» и «Пробка» совпадали. Однако способы действия, которыми достигался этот результат, были совершенно различными. В задаче «6 спичек» нужно было от построений в плоскости перейти к построениям в трехмерном пространстве. В задаче же «Пробка» уже в условиях определялось, что тело должно быть объемным, и нужно было только найти его форму.
В результате опытов обнаружилось, что задача «Пробка», данная в качестве наведения к задаче «6 спичек», на ее решение не влияла.
Возвращаясь к первой задаче, испытуемые не могли ее решить, хотя только что буквально держали ответ на эту задачу в собственных руках (тетраэдр/вылепленный из пластилина). Если тут же испытуемым давалась задача «Коробки», то вслед за ее решением задача «6 спичек» решалась. Вот один из протоколов (исп. Т. Р.).
Исп. (В течение 10 мин решает задачу «6 спичек» на плоскости). Затем прерывается экспериментатором, активность сохраняется),
Эксп. Все, ваше время кончилось. Можно вам предложить еще одну задачу? (Дает задачу «Пробка».)
Исп. (Вскоре решает ее.) Вот, а со спичками я хочу подумать для себя. (Берет спички, продолжает решать.) Нет, здесь какой-то фокус. Не знаю, как ее решить. Отказываюсь.
Эксп. Еще одну задачу, хотите?
Исп. Давайте. (Дается задача «Коробки», исп. в течение 15 минут решает ее на плоскости, наконец ставит коробки.) Так вот в чем дело! А я то... Как же все-таки спички решаются?! (Строит тетраэдр.)
Итак, готовый результат решения задачи оказался гораздо менее эффективным в качестве подсказки, чем способ действия, приводящий к тому же результату.
Нельзя сказать, что наглядное решение задачи вовсе не может выступить в функции наведения. Так, в некоторых известных случаях изобретений, в том числе приведенных нами выше, один вид какого-либо предмета подсказывал изобретателю, каким должно быть решение его задачи. То, что в наших опытах вид тетраэдра ни в одном случае не привел испытуемого к решению задачи «6 спичек», можно объяснить невозможностью создать в лабораторных условиях той аффективной напряженности, которая сопровождает поиски решения настоящих творческих задач. Но тем ярче на этом фоне выступают преимущества принципа решения задачи перед ее наглядным решением. Даже в искусственных условиях опыта принцип решения во всех случаях оказывал наводящее действие на решение основной задачи.
Итак, в изложенных экспериментах оказались выявлены некоторые условия, определяющие действие подсказки.
Для того чтобы наведение на правильное решение задачи состоялось, необходимо наличие следующих условий:
1) сохранение длительного стойкого интереса к задаче;
2) заключение о неэффективности первоначально применявшихся способов решения и отказ от них;
3) относительная новизна или неожиданность появления наводящих объектов или обстоятельств;
4) содержание в подсказке принципа решения основной задачи.
Оказалось также, что только сочетание всех перечисленных условий обеспечивает решение задачи. Несоблюдение одного из них сводит на нет положительное действие остальных условий.
Экспериментальный анализ психологических моделей творчества был продолжен в последующих работах Я. А. Пономарева, основной из которых является «Психология творческого мышления» (1960). Испытуемым предлагались задачи, решить которые можно только с помощью «подсказок». Одни из них — прямые указания к действию — не представляли особого интереса, здесь исчезала ситуация творческой задачи (опираясь на такую «подсказку», испытуемый решал задачу логически). Прямое содержание другой группы «подсказок» не имело «существенной» связи с задачей, связь заключалась в «случайном» признаке, например в совпадении движения руки при выполнении «подсказки» и при решении задачи.
Использование такого рода «подсказок» обнаружило факт, ставший отправным для построения моделей творческой ситуации. Как уже говорилось, «подсказка», предшествующая задаче, остается неэффективной, но если она следует за задачей, то при повторном обращении испытуемого к задаче «подсказка», оставаясь по ее объективному содержанию той же самой, как бы превращается в иную, функционально уподобляясь непосредственным указаниям к действию.
В основу гипотезы, характеризующей исследуемый механизм, положен факт неоднородности результата действия в ситуации «подсказки» — наличия в нем прямого (осознаваемого) и побочного (неосознаваемого) продуктов.
Было' сделано предположение, что в случае, когда «подсказка» предшествует задаче, часть результата действия в ситуации «подсказки», являющаяся ключом к решению задачи, оказывается на положении побочного продукта, не осознается и не может быть непосредственно использована как средство решения задачи. Однако при определенных условиях возникает возможность осознания этой части результата действия.
Таким образом, проблема психологического механизма решения творческой задачи выступила как проблема психологического механизма взаимоотношения прямого и побочного продуктов действия, определения конкретных условии превращения побочного продукта действия в прямой.
Исследование особенностей ориентировки в задании в зависимости от того, на какую часть субъективного результата предшествующего действия она опирается, показывало, что наряду с отражением прямого продукта действия отражается и его побочный продукт, а также качественное различие отражения того и другого.
При ориентировке, опирающейся на отражение прямого продукта действия, испытуемый уверен в успехе решения задания и всегда способен дать правильный отчет в своих действиях. Успех ориентировки не зависит ни от повторений «подсказки», ни от того интервала времени, который разделяет «подсказку» и выявляющее ее эффект задание.
Ориентировка, опирающаяся на отражение побочного продукта, имеет совершенно иные особенности: отсутствует какая-либо уверенность в успехе; абсолютно необходима чувственная основа; испытуемые не могут обосновать свои действия, более того, такая задача нарушает нормальный ход ориентировки; совершенство ориентировки оказывается зависимым от числа повторений «подсказки», ориентировка разрушается, если интервал между «подсказкой» и выявляющим ее заданием оказывается продолжительным.
Перевод побочного продукта действия на положение прямого; оказывается возможным в том случае, когда «подсказка» предваряется задачей, т. е. когда вначале дается задача, выступающая здесь в стимулирующей функции; затем следует «подсказка»; наконец — вновь задача, выступающая теперь уже в выявляющей функции. Под воздействием стимулирующей задачи у испытуемого возникает поисковая доминанта, определяющая ход ориентировки в ситуации «подсказки». Вместе с тем в опытах было установлено, что предварение «подсказки» стимулирующей задачей приводит к решению выявляющей задачи далеко не во всех случаях.
Варьирование условий эксперимента вскрыло, помимо уже известных закономерностей, целый ряд новых зависимостей.
1. Чем больше прямой продукт действия в «подсказке» удовлетворяет той или иной потребности субъекта, тем меньше вероятность переориентировки на побочный продукт и тем резче угасает поисковая доминанта, вызванная стимулирующей задачей.
2. Введение усложнений в ситуацию стимулирующей задачи искажает формируемую под ее влиянием поисковую доминанту; простота стимулирующей задачи — фактор, благоприятствующий преобразованию побочного продукта действия в прямой.
3. Аналогичным образом решению способствует простота выявляющей задачи.
4. Чем менее автоматизирован этот способ действия, которым выполняется «подсказка», тем в большем числе случаев осознается побочный продукт действия. 5. Успех решения зависит и от особенностей того способа, в который преобразуется при переходе к выявляющей задаче образованный в ситуации «подсказки» побочный продукт действия: чем более обобщенным оказывается этот способ, тем легче становится перенос.
С. Л. Рубинштейн ОСНОВНАЯ ЗАДАЧА
И МЕТОД ПСИХОЛОГИЧЕСКОГО
ИССЛЕДОВАНИЯ МЫШЛЕНИЯ
Основная задача психологического исследования мышления заключается в том, чтобы, не ограничиваясь фиксацией внешних результатов мыслительной деятельности, вскрыть самый процесс мышления во внутренних закономерностях его протекания.
Это — генеральная линия. Она реализуется в отношении ряда проблем, где исследование умственной деятельности сводилось к описанию ее внешнего протекания, к констатации фактов, в которых она выражается, без раскрытия внутреннего закономерного процесса, приводящего к этим фактам. Показательным примером может служить проблема «переноса».
В педагогической практике учитель часто встречается с тем, что ученик, решивший задачу или как будто усвоивший теорему применительно к данным условиям, оказывается не в состоянии «перенести» это решение в другие условия, решить ту же задачу, как только задача предъявляется ему в видоизмененных условиях. Это часто встречающийся и практически фундаментально важный факт. С констатации подобных фактов начинает, как известно, свое исследование о «продуктивном мышлении» Вертгеймер. На нем останавливались и авторы ряда исследований, публиковавшихся в нашей психологической литературе. Чрезвычайно важно поэтому выяснить его причины.
Под переносом обычно разумеют применение сложившегося у индивида и закрепленного в виде навыка способа действия в новых условиях, при решении других аналогичных задач. Однако и закрепляющийся в виде навыка способ решения задачи должен быть сперва найден. Поэтому в конечном счете в плане мышления проблема «переноса» преобразуется в проблему применения прежде найденных решений (знаний) к новым задачам.
За фактами отсутствия переноса решения с одной задачи на другую, ей аналогичную, стоит недостаточный анализ условий задачи соотносительно с ее требованиями и вытекающая отсюда недостаточная обобщенность решения.
Условия, в которых дается задача, включают обычно в более или менее нерасчлененном виде собственно условия задачи, т. е. те данные, которые участвуют в решении, с которым это последнее необходимо связано, и ряд привходящих обстоятельств (то или иное расположение чертежа, та или иная формулировка задачи и т. п.).
Для того чтобы решение задачи оказалось для учащегося (испытуемого) переносимым на другие случаи, отличающиеся от исходных лишь несущественными, привходящими обстоятельствами (тем или иным расположением фигур и т. п.), необходимо (и достаточно), чтобы анализ через соотнесение с требованиями задачи вычленил собственно условия задачи из различных привходящих обстоятельств, в которых они непосредственно выступают сначала. Невозможность переноса решения в другую ситуацию (при изменении положения фигуры и т. п.) объясняется отсутствием такого анализа и отсюда вытекающей недостаточной обобщенностью решения задачи. Мало того, для того чтобы реализовать даже обобщенное решение в новых обстоятельствах, нужно не просто его «перенести», а, сохраняя его по существу, соответственно соотнести его с этими обстоятельствами, т. е. проанализировать и их (иногда через это соотнесение осуществляется и самое обобщение решения, выступающее в этом случае как результат синтетического акта).
В основе переноса лежит обобщение, а обобщение есть следствие анализа, вскрывающего существенные связи. Анализа требуют как сама задача, условия, в которых она первоначально решается, так и те видоизмененные условия, на которые это решение переносится.
С переносом решения одной и той же задачи в разные условия (обстоятельства) тесно связан перенос решения из одной задачи на другую, однородную с ней в том или ином отношении. Этот последний случай был подвергнут у нас специальному исследованию.
Опыты К. А. Славской показали, что перенос совершается в том и только в том случае, когда обе задачи соотносятся и включаются испытуемыми в процессе единой аналитико-синтетической деятельности. Конкретно это выражается в том, что условия одной задачи анализируются через их соотнесение с требованиями другой. Для осуществления переноса решения требуется обобщение, связанное с абстракцией от несущественных моментов первой задачи и конкретизацией его применительно ко второй. Главную роль при переносе играет анализ основной задачи, подлежащей решению. Течение процесса обобщения и осуществление переноса зависят главным образом от степени проанализированности той основной задачи, на которую должен быть совершен перенос. Если вспомогательная задача предъявлялась на начальных этапах анализа основной, то она решалась сперва самостоятельно, безотносительно ко второй; обобщение совершалось в результате развернутого соотнесения свойств и отношений обеих задач. Если вспомогательная задача предъявлялась, когда анализ основной задачи был уже значительно продвинут, то вспомогательная задача решалась сразу через соотнесение с требованиями основной, как звено этой последней. В этом случае обобщение совершается в ходе решения вспомогательной задачи.
Эксперимент, в ходе которого это вскрылось, велся следующим образом: экспериментатор предлагал испытуемому решить задачу, рассуждая вслух; ход рассуждений испытуемого при решении задачи подробно протоколировался. Испытуемым — учащимся 7—9-х классов средних школ — давалась основная задача: доказать равновеликость треугольников АВО и OCD, заключенных между диагоналями трапеции (решение ее заключается в выделении треугольников ABD и ACD, которые равновелики, так как имеют общее основание AD и общую высоту трапеции, искомые треугольники являются частью данных и поэтому равновелики) (рис. 1). Для исследования переноса решения с одной задачи на другую испытуемым в ходе решения одной (основной)


Рис. 1 Рис. 12
задачи давалась другая вспомогательная. В экспериментальную группу включались только те из обследованных испытуемых (48 школьников и 12 студентов), которые решали основную задачу с помощью вспомогательной и на которых поэтому можно было прослеживать ход переноса. Во вспомогательной задаче нужно было доказать равенство диагоналей прямоугольника ABCD. Они равны, так как равны треугольники ABD и ACD, имеющие общее основание AD, равные стороны АВ и CD и равные прямые углы (рис. 2). Основная задача решается с помощью вспомогательной посредством переноса на нее решения вспомогательной задачи. Общим звеном в решении обеих задач было использование общего основания AD треугольников ABD и ACD, которое в одном случае используется как общее основание равных, в другом — равновеликих треугольников. Таким образом, чтобы решить основную задачу, т. е. найти равновеликие фигуры, связанные с искомыми и имеющие равные (общие) высоты и общее основание, нужно выделить это звено решения вспомогательной задачи как общее для обеих задач, т. е. произвести обобщение.
Поэтому нет нужды в специальном применении одной задачи к другой: перенос осуществляется с места, сразу.
Чтобы проследить зависимость обобщения от анализа основной задачи, вспомогательная задача предъявлялась испытуемым на разных этапах анализа основной.
В качестве ранних этапов в специальном, узком смысле слова мы выделяли те, на которых испытуемые оперировали, анализировали и т. д. лишь с тем, что было непосредственно дано в условиях задачи; под поздними этапами анализа мы соответственно разумели те стадии решения задачи, на которых испытуемые уже выделяли новые условия, выходящие за пределы того, что было непосредственно дано в исходных условиях задачи.
Конкретно различение более ранних и более поздних этапов анализа основной задачи в наших экспериментах осуществлялось следующим образом.
Одной части испытуемых вспомогательная задача давалась в тот момент, когда они анализировали непосредственно данные в задаче условия, т. е. на ранних этапах анализа задачи. Эти испытуемые проводили высоты треугольников АВО и OCD и анализировали их равновеликость, т. е. пытались доказать равенство их высот и оснований (рис. 3). Вначале, следовательно, они анализировали то, что непосредственно дано в условии задачи — равновеликость треугольников АВО и OCD.
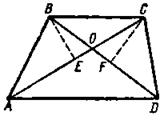
Рис. 3
В ходе проб испытуемые убеждались в невозможности доказать равновеликость АВО и OCD через равенство их высот и оснований. Они продолжали анализировать задачу дальше, выявляли новые, не данные им условия. Так, они выделяли другие фигуры, связанные с искомыми, чтобы первоначально доказать их равновеликость, рассматривали их высоты и основания (например, треугольников ABD и BCD с общей высотой трапеции и основаниями, которые являются верхним и нижним основаниями трапеции). Это выделение в ходе анализа задачи новых условий мы принимали за поздние этапы, анализа задачи. Второй группе испытуемых вспомогательная задача предъявлялась на этих поздних этапах анализа основной.
Чтобы «перенести» решение с одной задачи на другую, нужно найти обобщенное решение обеих задач. Предъявляя вспомогательную задачу на разных этапах анализа основной задачи, мы прослеживали, как осуществляется обобщение в зависимости от степени проанализированности основной задачи, зависимость обобщения от анализа.
Испытуемые первой группы, которым вспомогательная задача предъявляется на ранних этапах анализа основной, решают вспомогательную задачу как самостоятельную, не связанную с основной. После решения вспомогательной задачи испытуемые возвращались к решению основной задачи. При этом большая часть испытуемых начала соотносить дальнейшее решение основной задачи со вспомогательной.
Таким образом, получается, что начальные этапы, или низшие уровни мышления, сами создают предпосылки, которые ведут к высшим. «Мотивом», побуждавшим к этому соотнесению, служило то, что испытуемые уже до осуществления сколько-нибудь развернутого и углубленного соотнесения задач усматривали, что между обеими задачами есть что-то общее, раскрывающееся затем в результате этого соотнесения, так как никаких указаний на связь обеих задач испытуемым не давалось; более того, чтобы не наводить испытуемых на эту мысль, экспериментатор предъявлял вспомогательную задачу с нарочито маскировочной установкой, говоря испытуемым, что вторая вспомогательная задача дается им для передышки. Следовательно, оказывается, что сам ход решения, задачи создает внутренние условия для дальнейшего движения мысли, причем эти условия включают в себя не только предпосылки логически-предметные, но и мотивы мышления, «двигатели» его. Соотнесение (синтез) задач осуществлялось так, что,продолжая решение основной задачи, испытуемые анализировали в ней те же геометрические элементы (углы, равные стороны, равные диагонали), которые они использовали при решении вспомогательной задачи.
Так, например, испытуемый Д. В. говорит:
«Здесь же трапеция — совсем другое дело. Здесь диагонали не равны и боковые стороны тоже. Я не знаю, чем мне здесь могут помочь диагонали...» ' (протокол № 17).
Протоколы показывают, что, анализируя условия основной задачи, испытуемые, выделяют элементы, использовавшиеся во вспомогательной задаче, для доказательства равенства треугольников. Все испытуемые анализируют в условиях основной задачи общие, сходные со вспомогательной задачей условия. Условия основной задачи анализируются через соотнесение с требованием вспомогательной.
Испытуемый Д. В. говорит: «Мне нужно доказать равновеликость треугольников».
Испытуемый переходит к анализу новых условий, убеждаясь вневозможности использовать для решения данные в условии задачи треугольники. «Очевидно, что прямо и через равенство данных треугольников доказать нельзя, — говорит он, — может быть, можно через треугольники ABD и ACD?». Так испытуемый Д. В. переходит к выявлению новых условий основной задачи. Это создает предпосылки для привлечения новых условий из вспомогательной задачи (через соотнесение с требованием основной). Из всех найденных в ходе предшествующего анализа геометрических элементов (равных сторон, диагоналей и т. д.) привлекается к решению основной задачи только общее основание AD — для доказательства равновеликости треугольников ABD и ACD. Испытуемый Д. В. говорит: «Равенство углов нам не нужно, равенство диагоналей тоже не нужно, а общее основание мы можем использовать».
Таким образом, испытуемый выявляет то общее звено решения, которое является существенным и для основной задачи. Происходит обобщение — в геометрическом элементе, использовавшемся при решении вспомогательной задачи (для доказательства равенства), выявляется новое свойство, существенное с точки зрения требования основной задачи (для доказательства равновеликости треугольников). Таким образом, оказывается, что ни одно из звеньев решения вспомогательной задачи не привнесено извне в основную задачу; каждое звено решения основной задачи оказывается выявленным в результате анализа самой основной задачи, ее условий, ими обусловленных отношений ее элементов, поэтому оно выделяется как общее, т. е. отвечающее требованию основной задачи, т. е. существенное для нее. Так происходит движение анализа от выявления общего как сходного к выделению общего, существенного для основной задачи.
Итак, при предъявлении вспомогательной задачи на ранних этапах анализа основной испытуемые первой группы решают вспомогательную задачу как самостоятельную, не связанную с основной. Обобщение совершается постепенно в ходе дальнейшего анализа основной задачи, осуществляющегося через соотнесение сначала с требованием вспомогательной, затем основной задачи. Движение процесса совершается от выявления сходного к выделению существенного через анализ и соотнесение обеих задач.
Вторая группа испытуемых, которая получила вспомогательную задачу на поздних этапах анализа основной задачи, решала вспомогательную задачу не как самостоятельную, а как непосредственное продолжение основной.
Так, например, решая вспомогательную задачу, где надо доказать равенство диагоналей, рассмотрев равенство треугольников, испытуемая Л. Г. говорит: «Они равны, т. е. у них общее основание, АВ и CD — общие высоты» (протокол № 16).
Таким образом, испытуемая абстрагировалась от всех моментов (равенство углов и треугольников), которые были несущественны для основной задачи, где речь шла не о равенстве, а о равновеликости. Вместе с тем те прямые, которые во вспомогательной задаче являются сторонами, она обозначает как равные высоты и общее основание, т. е. сразу выделяет их в связи с основной задачей, связывает их и с доказательством равенства (как того требовала вспомогательная задача), и с доказательством равновеликости (в соответствии с требованием основной задачи). Испытуемая Л. Г. анализирует условия вспомогательной задачи не только через соотнесение с ее собственным требованием, но и одновременно с требованием основной задачи.
В этом случае обобщение совершается уже в ходе решения вспомогательной задачи. Решение вспомогательной задачи служит как бы ответом на основную задачу, включается как недостающее звено анализа в решении последней. Обобщение совершается «с места», сразу, и нет необходимости в специальном действии применения одной задачи к другой. Это говорит о том, что именно обобщение, совершающееся при решении вспомогательной задачи, составляет истинную сущность того, что обозначается как перенос решения из задачи в задачу.
Таким образом, при предъявлении вспомогательной задачи на поздних этапах анализа основной вспомогательная задача решается испытуемыми второй группы уже не как самостоятельная, а в связи с основной. Условия вспомогательной задачи анализируются через соотнесение с требованием основной задачи, а не только через соотнесение с ее собственным требованием. В силу того, что основная задача проанализирована испытуемыми до предъявления вспомогательной, они сразу выделяют одно из звеньев решения вспомогательной задачи как существенное для основной задачи: обобщение совершается сразу в ходе решения вспомогательной задачи.
Таким образом, сравнивая результаты экспериментов, проведенных с двумя группами испытуемых (получившими вспомогательную задачу на ранних и на поздних этапах анализа основной), можно сказать следующее. От степени проанализированности основной задачи зависит то, как конкретно совершаются обобщение и перенос, к которому приводит обобщение: развернуто, постепенно, в результате анализа элементов и отношений обеих задач или уже в ходе решения вспомогательной задачи «с места», сразу. Следовательно, от анализа основной задачи зависит, когда и как совершается обобщение. Это говорит о зависимости обобщения от анализа. Ход анализа основной задачи определяет, как совершится обобщение задач.
Однако, как видно из рассмотренного экспериментального материала, обобщение подготовляется не в ходе анализа одной только основной задачи. Анализ того же экспериментального материала выявил также, что основным условием обобщения является включение обеих задач в единую аналитико-синтетическую деятельность.
Только единая аналитико-синтетическая деятельность, включающая обе задачи, приводит к выделению общих звеньев, т. е. к переносу.
Эта закономерность была не среднестатистической, а всеобщей закономерностью. Она выступила у всех без исключения 38 испытуемых, которым вспомогательная задача предъявлялась после основной, так же как и у всех 10, которым она предъявлялась до основной задачи. Та же закономерность, полученная сначала на основной группе испытуемых (школьников), проявилась и у 12 студентов, с которыми для сравнения проводились те же эксперименты.
...Исследование наше показало, что, как уже отмечалось, продуктивное соотнесение вспомогательной задачи с основной совершается только на поздних этапах анализа последней. Это положение имеет, с нашей точки зрения, принципиальное значение, поскольку оно, по существу, означает, что использование «подсказки», заключенной во вспомогательной задаче, может быть совершено лишь тогда, когда анализ самой подлежащей решению задачи создал для этого внутренние условия.
Между тем это положение вступило как будто бы в противоречие с данными другого нашего исследования, проводившегося Е. П. Кринчик. В ее экспериментах широко и систематически использовалось предъявление испытуемым, затруднявшимся в решении поставленной перед ними задачи, задач вспомогательных. В опытах Кринчик вспомогательные задачи предъявлялись испытуемым как до, так и после предъявления основной. Помимо этих экспериментальных данных и теоретические соображения как будто говорят за то, что предъявление вспомогательной, наводящей задачи, с которой решение переносится на основную, является важнейшим, привилегированным, основным, так как именно с этим случаем мы имеем дело при использовании прошлого опыта. Однако эти результаты экспериментов Е. П. Кринчик находятся в прямом противоречии с данными других исследований (Я. А. Пономарева, Ю. Б. Гиппенрейтер), согласно которым предъявление наводящей задачи оказывалось эффективным только при предъявлении ее после основной.






