Складывать (вычитать) можно только матрицы одного размера, результатом будет матрица того же размера.
Пусть даны две матрицы  и
и  одинакового размера, необходимо найти матрицу
одинакового размера, необходимо найти матрицу  , равную их сумме.
, равную их сумме.

На листе Excel в ячейках A2:C3 разместим матрицу  , в ячейках E2:G3 – матрицу
, в ячейках E2:G3 – матрицу  . Для матрицы-результата
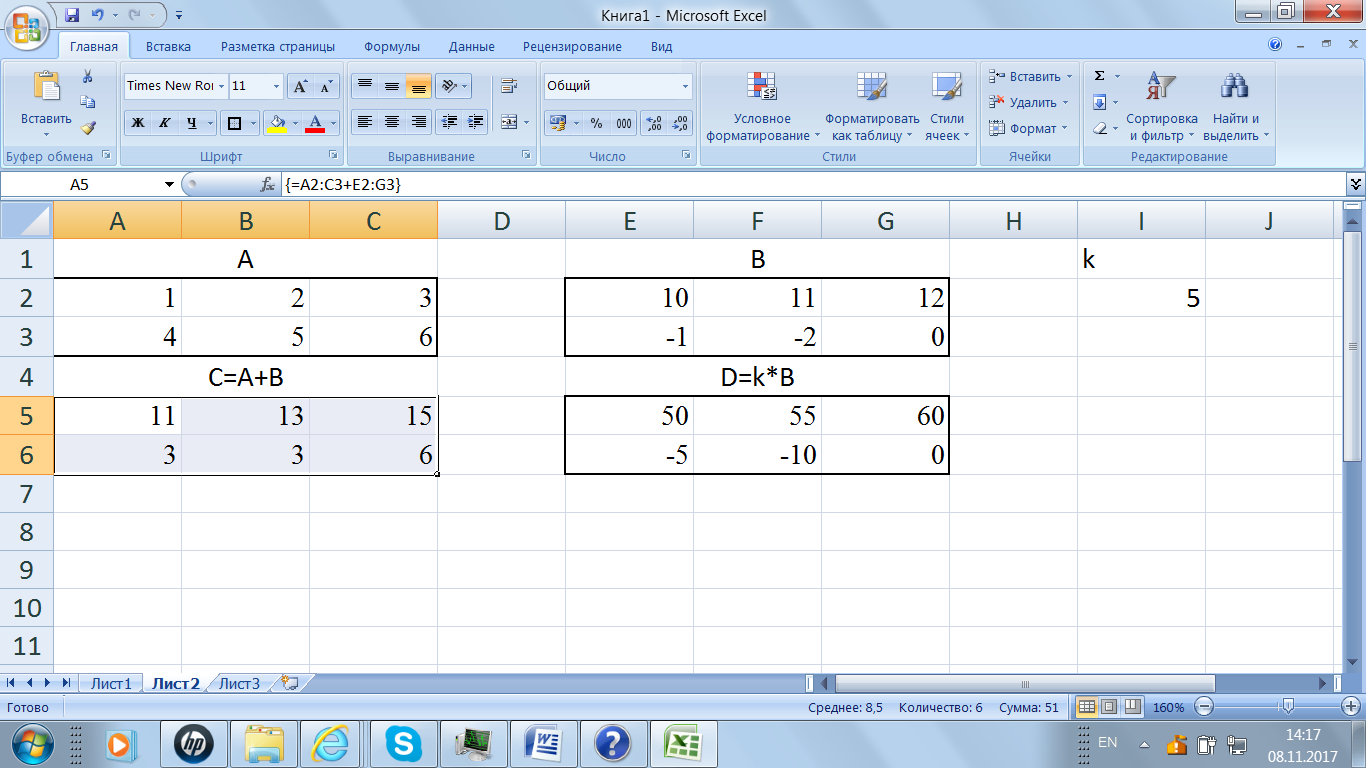
. Для матрицы-результата  выделим диапазон A5:C6. Операцию «сложение» («вычитание») реализуем как операцию над массивами. Для этого в ячейку A5 вводим формулу:
выделим диапазон A5:C6. Операцию «сложение» («вычитание») реализуем как операцию над массивами. Для этого в ячейку A5 вводим формулу:
=A2:C3 + E2:G3
Операция завершается одновременным нажатием трех клавиш CTRL+ SHIFT+ENTER. Для вычисления разности двух матриц в формуле меняется знак «+»на «-» (рис. 37).
Для умножения (деления) матрицы на число k формула будет иметь вид:
= (A2:C3)*k или = (A2:C3)/k
 Операция завершается нажатием клавиш CTRL+ SHIFT+ENTER.
Операция завершается нажатием клавиш CTRL+ SHIFT+ENTER.
Рис. 37. Сложение матриц и умножениематрицы на число
Перемножение матриц
Операция перемножения двух матриц определена, если число столбцов первой матрицы равно числу строк второй. Результирующая матрица будет иметь число строк, равное числу строк первой матрицы, а число столбцов, равное числу столбцов второй матрицы.

Разместим матрицы  и
и  соответственно в диапазонах A2:C3, E2:F4; под матрицу результата выделим диапазон L2:M3. В ячейке L2 записываем обращение к функции (рис. 38)
соответственно в диапазонах A2:C3, E2:F4; под матрицу результата выделим диапазон L2:M3. В ячейке L2 записываем обращение к функции (рис. 38)
= МУМНОЖ ()

Рис. 38.Окно команды умножения матриц
В диалоговое окошко функции МУМНОЖ вводим диапазон первой матрицыA2:C3в рабочее поле «Массив 1» (указателем мыши при нажатой левой кнопки), в рабочее поле «Массив 2»– диапазон второй матрицы E2:F4.Завершаем операцию одновременным нажатием клавиш CTRL+ SHIFT+ENTER (рис. 39).

Рис. 39.Итоговая матрица 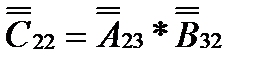
Операция обращения матрицы
Обратной матрицей кматрице  , называется такая матрица
, называется такая матрица  , которая будучи умноженной на исходную как справа, так и слева, дает единичную матрицу, т.е.
, которая будучи умноженной на исходную как справа, так и слева, дает единичную матрицу, т.е.

Необходимые условия существования обратной матрицы:
1. Исходная матрица должна быть квадратной.
2. Исходная матрица должна быть невырожденной, т.е.определитель матрицы отличен от нуля.
Разместим исходную квадратную матрицу размера 3*3 в ячейках A2:C4, вычислим ее определитель с помощью команды =МОПРЕД() и поместим его в ячейку E2. Определитель отличен от нуля и равен 11. Следовательно, для исходной матрицы существует обратная. Найдем ее с помощью команды =МОБР(). Предварительно выделим место под обратную матрицу A7:C9 (рис. 40).

Рис. 40. Нахождение обратной матрицы
В ячейках A7:C9 будет обратная матрица. Для проверки правильности вычисления обратной матрицы приведены результаты умножения (рис. 41):

Рис. 41. Обратная матрица и результаты проверки




