Ниже приводится определение и пример записи матрицы.
Матрица
| Совокупность элементов, расположенных в прямоугольной таблице, состоящей из n строк и m столбцов, называется матрицей и обозначается как |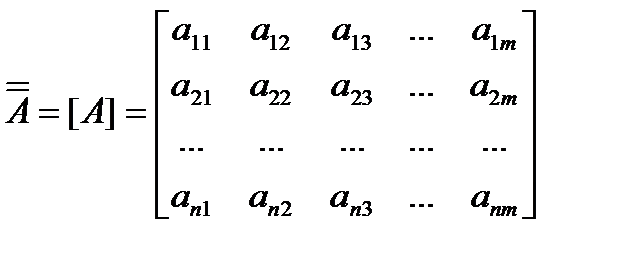 
|
Положение элемента aij в матрице определяется двумя индексами (i и j), где i определяет номер строки, а j – номер столбца.
Частный случай матрицы – вектор-столбец или вектор-строка; имеют один столбец (строку) и n строк (столбцов).
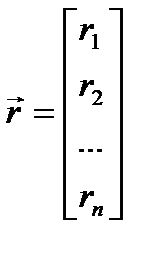или 
Далее и матрицу, и вектора будем называть массивом, двумерным или одномерным, соответственно. Числовые характеристики матриц можно рассчитать с использованием встроенных функций Excel. Важнейшими числовыми характеристиками матрицы являются норма и определитель.
Определитель матрицы (det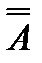 
) – это число, поставленное в соответствие квадратной матрице порядка n и равное сумме n! слагаемых, каждое из которых вычисляется как произведение n элементов матрицы, взятых по одному из каждого столбца и каждой строки.Знаки определяются в соответствии с правилами линейной алгебры.Для вычисления определителя воспользуемся встроенной функцией МОПРЕД (рис. 33).
Матрицу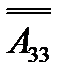 
разместим в диапазоне A 3: C 5. Для результата выделим одну ячейку A 7. В этой ячейке записываем знак «=» (как начало выражения), открывается окно «Мастер функции», выбираем функцию МОПРЕД.В окне аргумента функцииМОПРЕД(…) указываем диапазон ячеек размещения исходной матрицы. Завершаем операцию одновременным нажатием клавиш CTRL+SHIFT+ENTER (рис. 34).
Рис. 33.Вызов встроенной функции МОПРЕДчерез мастера функций
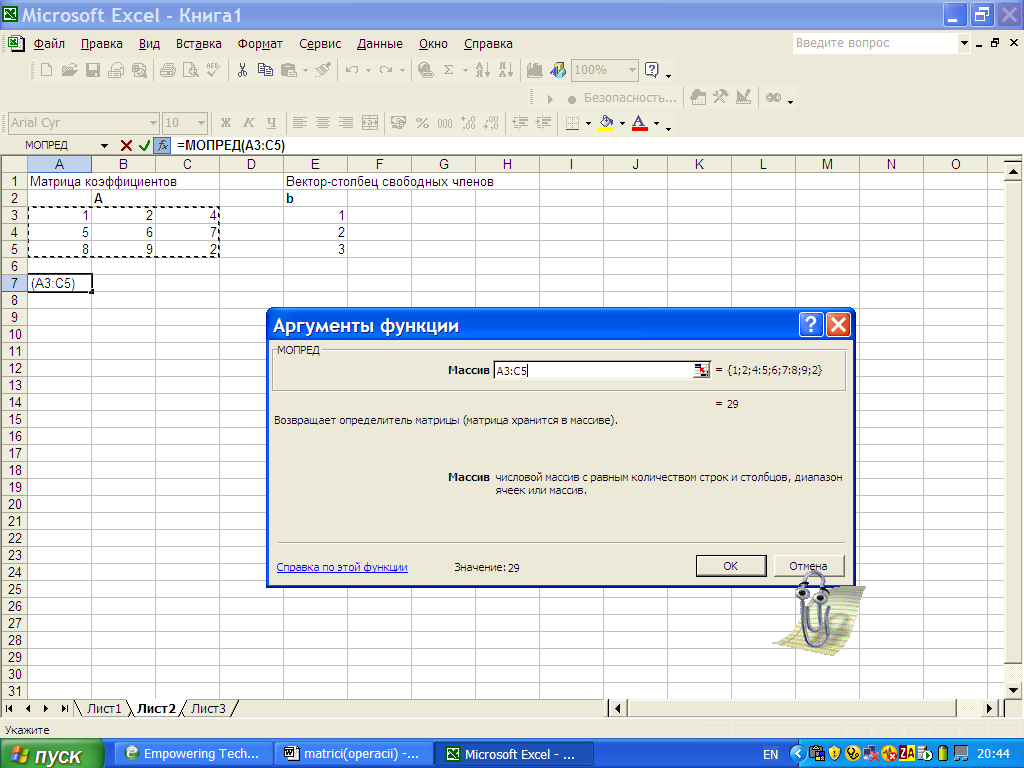
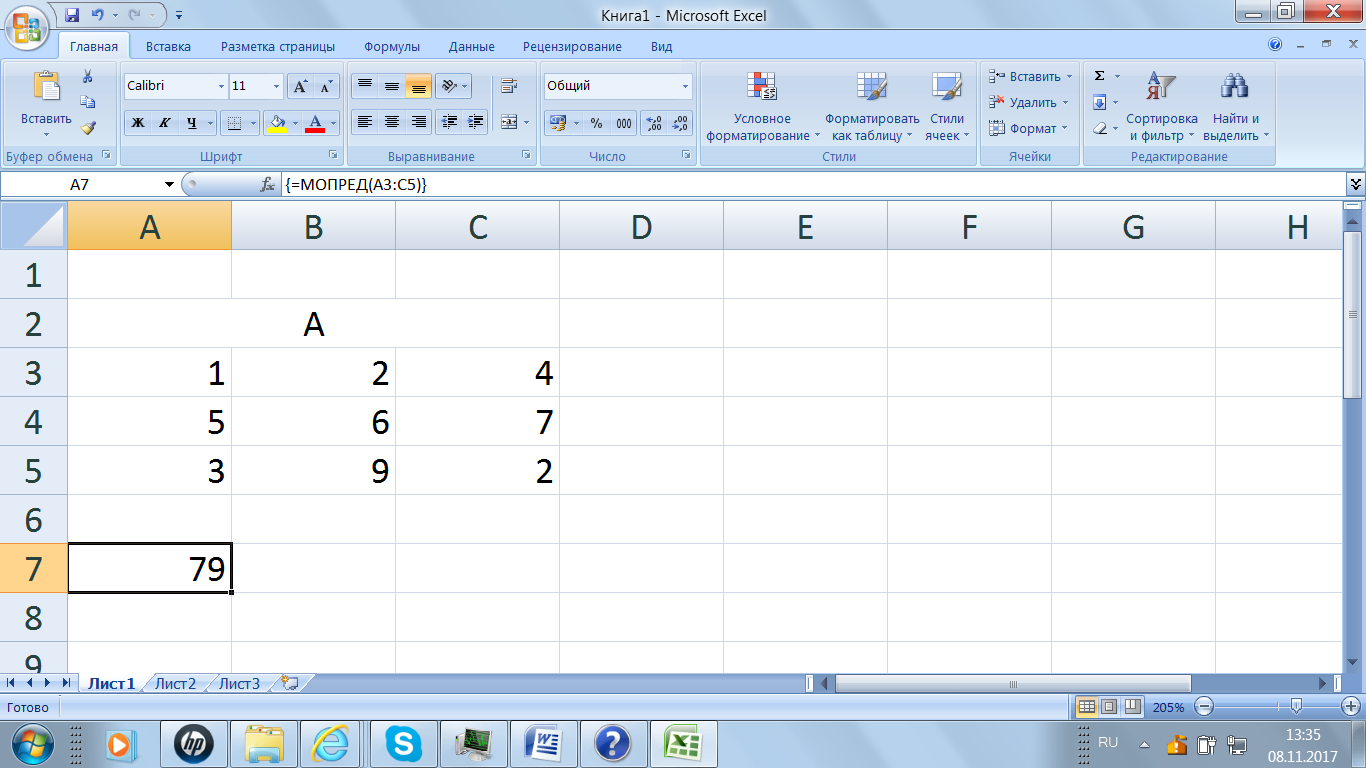
Рис. 34.Использование встроенной функции МОПРЕД для вычисления
определителя матрицы
Понятие нормы существуеткак для матриц, так и для векторов. Рассмотрим примервычисления часто используемой Евклидовой нормы для матрицы.Евклидова норма – это число, равное значению выражения:
т.е. корень квадратный из суммы квадратов всех элементов матрицы.
Для вычисления Евклидовой нормы воспользуемся встроенной функцией СУММКВ. В ячейку, выделенную под значение нормы, введем выражение
=СУММКВ(…)^0.5
изавершим операцию одновременным нажатием клавиш CTRL+SHIFT+ENTER.
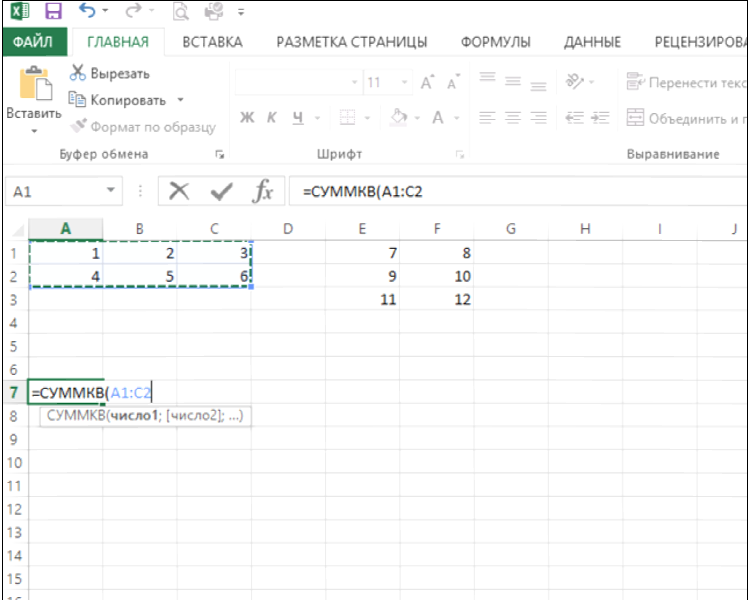
Рис.35.Вычисление Евклидовой нормы матрицы
Транспонирование матриц
Транспонированной матрицей к матрице (
)называется такая матрица (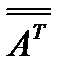
), в которой элементы строки исходной матрицы заменяются элементами соответствующего столбца, т.е.
= 
,
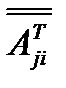где i=1,2,……,m, j=1,2,…,n.
Пусть исходная матрица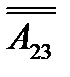 
записана в диапазоне ячеек A2:C3; для транспонированной матрицы выделим диапазон A6:D8. Для операции транспонирования воспользуемся встроенной функцией ТРАНСП, которую вводим в строку формул:
=ТРАНСП()
В строку «Массив» окна «Аргументы функции» вводим диапазон ячеек исходной матрицы 
. Завершаем операцию одновременным нажатием клавиш CTRL+Shift+Enter.
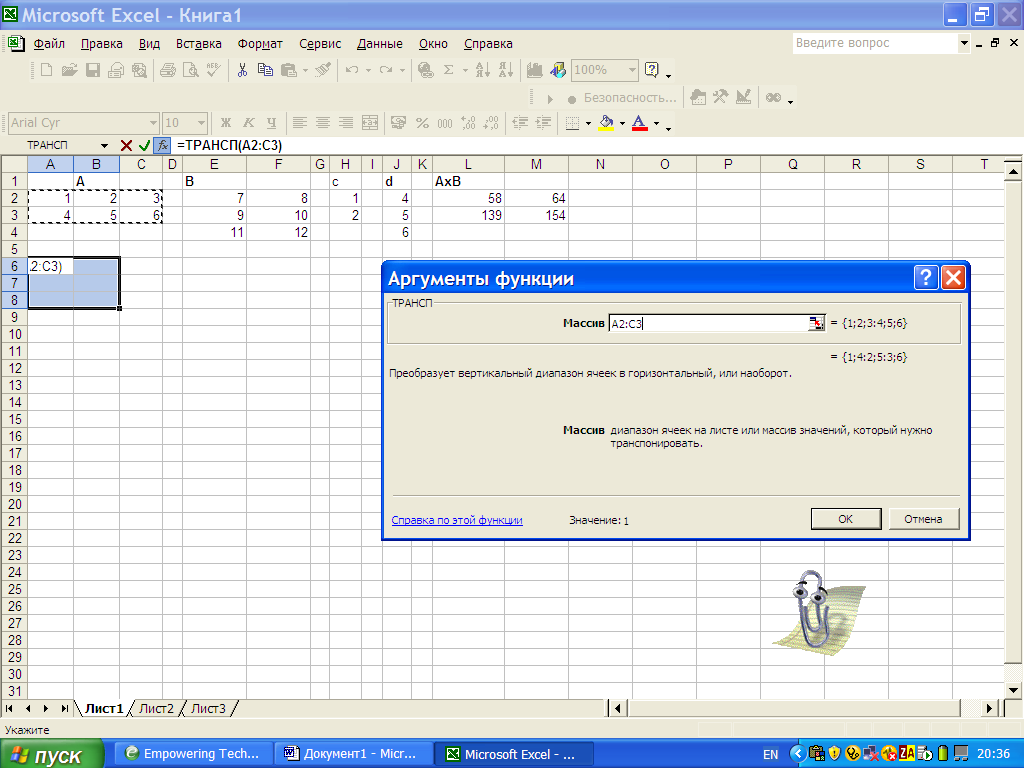
Рис. 36. Транспонирование матрицы
