В общем виде СЛАУ можно записать в следующем виде
Будем рассматривать нормальную и определенную СЛАУ, т.е. систему, имеющую единственное решение и число уравнений которой равно числу неизвестных, т. е. n = m. В качестве примераграфической иллюстрации, совместной и определенной СЛАУ рассмотрим систему из двух уравнений:
2x1 + x2 = 3
2x1+ 2x2 = 4
Ниже приведен график, иллюстрирующий единственное решение: одна точка пересечения двух прямых (рис. 42):
Рис. 42.Пример решения совместной и определенной СЛАУ
Для решения СЛАУ воспользуемся методом обратной матрицы.
Запишем систему уравнений в матричном виде:
Совокупность коэффициентов системы можно представить в виде матрицы 
:
, i=1,2,3,…,n; j=1,2,3,….,n
Совокупность неизвестных системы и свободных членов – в виде векторов:
, i=1,2,3,…,n 
, i=1,2,3,…,n
Решить СЛАУ значить найти такие значения вектора:
,
подстановка которого в систему, обращает каждое уравнение этой системы в тождество.Умножая левую и правую части матричного уравнения на обратную матрицу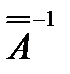 
, получим расчетное соотношение:
Для системы из трех уравнений найти решение методом с использованием обратной матрицы. На листе Excel в ячейках A2:C4 размещаем элементы матрицы коэффициентов системы (матрица 
), в ячейках E2:E4– элементы вектора-столбца свободных членов (вектор 
). Для вычисления обратной матрицы 
воспользуемся командой =МОБР(), предварительно выделив ячейки A7:C9. Далее выделяем ячейки E7:E9 для вектора решения и выполняем команду =МУМНОЖ()для перемножения обратной матрицы 
на вектор 
. На листе Excel приведена проверка правильности решения СЛАУ (рис. 43,44).
8x1– 13x2– 6x3 =4
–3x1+ 8x2–2x3 = 5
–x1–10x2 = –6
A= 
Рис. 43. Решение СЛАУ с проверкой решения
Рис. 44. Окно вычисления корней
П Р И Л О Ж Е Н И Я
П. 1. Приложение к разделу «Построение графиков»
П.1.1. Задания: построить график функции одной переменной, x Î [-5;5]:
Вариант 1: y=–0,1x3–0,16x2+8,04x+11,78
Вариант 2: y=–0,00142x5+0,006x4+0,39x3–1,09x2–2,81x+6,19
Вариант 3: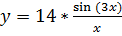 
Вариант 4: y=2*(cos(x)+2)^sin(x-2)-2.1;
Вариант 5: y=–0,16x3–0,15x2+7,62x+5,26
Вариант 6: y=–0,00388x5+0,005x4+0,28x3–1,03x2–4,61x+4,78
Вариант 7: 
Вариант 8: y=–2*(cos(1,5x)+2,5)sin(x-1)+1.5;
Вариант 9: y=–0,17x3–0,14x2+6,13x+18,48
Вариант 10: y=–0,00258x5+0,01x4+0,22x3–1,11x2–4,63x+7,76
Вариант 11: 
Вариант 12: y=1,2(sin(x)+2,2)cos(x+1)-1.2;
Вариант 13: y=–0,17x3–0,12x2+6,31x+3,83
Вариант 14: y=–0,00367x5+0,005x4+0,23x3–1,06x2–4,39x+8,99
Вариант 15: 
Вариант 16: y=1,4*(0,5cos(2x)+3)sin(x+3)-2;
Вариант 17: y=–0,13x3–0,12x2+6,63x+11,6
Вариант 18: y=–0,00185x5+0,008x4+0,27x3–1,01x2–4,80x+3,56
Вариант 19: 
Вариант 20: y=1,3(0,5cos(x)+1,5)atan(x)-1.5;
Вариант 21: y=–0,17x3–0,15x2+9,35x+12,44
Вариант 22: y=–0,00250x5+0,007x4+0,37x3–1,15x2–7,40x+6,59
Вариант 23: 
Вариант 24: y=1,4*(cos(3x)+2,8)atan(x+5)-5;
Вариант 25: y=–0,12x3–0,11x2+9,90x+6,64
Вариант 26: y=–0,00333x5+0,005x4+0,25x3–1,20x2–1,39x+2,47
Вариант 27: 
Вариант 28: y=5(0,4*sin(x)+1)atan(x-1)-5.5;
Вариант 29: y=–0,16x3–0,13x2+8,57x+17,30
Вариант 30: y=–0,00167x5+0,005x4+0,35x3–1,13x2–2,12x+4,81
П. 1.2. Задания: построить график функции одной переменной с двумя условиями.Использовать условный оператор «если».
Вариант 1. xÎ [–1,4;1,9]:
y = ((1+|x|)0,5)/(2+|x|) при x ≤ 0
y = (1+x)/(2+cos3(x)) при x > 0
Вариант 2. xÎ [–3,5;3,5]:
y = cos(3x)*sin(x) при x ≤ 0
y = cos2(x) – cos(3x) при x > 0
Вариант 3. xÎ[-1,7;1,5]:
y = (1+x2)0,5при x ≤ 0
y = (1+x)/(1+(1+ e0.2x)(1/3)) при x > 0
Вариант 4. xÎ [–3,5;3,5]:
y = 2cos(4x)*sin(2x) при x ≤ 0
y = cos2(3x) – cos(x)*sin(x) при x > 0
Вариант 5. xÎ[–2;1,8]:
y = (1 + x)/(1+ x2) при x ≤ 0
y = ((1+2x)/(1+x))0,5 при x > 0
Вариант 6. xÎ [–3,5;3,5]:
y = 3sin(3x)*cos(2x) при x ≤ 0
y = sin(x)*cos3(x) при x > 0
Вариант 7. xÎ[–1.8;1,8]:
y = (3 + sin(x))/(1+ x2) при x ≤ 0
y = 2x2cos2(x) при x > 0
Вариант 8. xÎ [–3,5;3,5]:
y = 2sin(x)* cos(x) при x ≤ 0
y = sin(3x)*cos2(x) при x > 0
Вариант 9. xÎ[–2;3,5]:
y = ((1 + 2x2)/(1+ x2))0,5при x ≤ 0
y = 2cos2(x) при x > 0
Вариант 10. xÎ [–3,5;3,5]:
y = 3sin(2x)*cos(x) – cos2(3x) при x ≤ 0
y = 2cos2(2x) – 3sin(3x) при x > 0
Вариант 11. xÎ[–2;1,5]::
y = 3x + (1+x 2)0,5при x ≤ 0
y = 2sin(3x) при x > 0
Вариант 12. xÎ [–3,5;3,5]:
y = 5sin(x) cos(3x)*sin(x) при x ≤ 0
y = cos(2x) – 2sin3(x) при x > 0
Вариант 13. xÎ[–3,5;2]:
y = 3sin(x) – cos2(x) при x ≤ 0
y = 3(1+x2)0,5 при x > 0
Вариант 14. xÎ [–3,5;3,5]:
y = 2sin(x)+ 3cos(x) приx ≤ 0
y = cos2(2x) – 2sin(x) при x > 0
Вариант 15. xÎ [–1,4;1,9]:
y = (1+|x|)/((x2 + x + 1)(1/3)) при x ≤ 0
y = 1 + ln(x2 + 1) при x > 0
Вариант 16. xÎ [–3,5;3,5]:
y = 6sin(x)*cos(x) приx ≤ 0
y = 3cos2(x)*sin(x) при x > 0
Вариант 17. xÎ[–1,2;1,7]:
y = ((1+|x|)0,5)/(5+|x|) при x ≤ 0
y = (1+x)/(2+cos2(x)) при x > 0
Вариант 18. xÎ [–3,5;3,5]:
y = cos(x)* sin(3x) при x ≤ 0
y = cos2(2x) – cos(3x) при x > 0
Вариант 19. xÎ[–1,5;1,7]:
y = (2+x2)0,5при x ≤ 0
y = (1+x)/(2+(1+ e0.3x)(1/3)) при x > 0
Вариант 20. xÎ [–3,5;3,5]:
y = 2cos(2x)*sin(4x) при x ≤ 0
y = cos2(x) – cos(x)*sin(3x) при x > 0
Вариант 21. xÎ[–1,3;1,3]:
y = (2+x)1/3; x<0
y = sin(2x)*cos(x); x≥0
Вариант 22. xÎ [–3,5;3,5]:
y = sin(x)*cos(2x) при x ≤ 0
y = 2cos(x)*sin(x) при x > 0
Вариант 23. xÎ[–1,8;1,5]:
y = (1+|x|)0,5 при x ≤ 0
y = (1+2x)/(1+(2+x)1/3) при x > 0
Вариант 24. xÎ [–3,5;3,5]:
y = 3sin(2x)*cos(3x) при x ≤ 0
y = cos2(x)*sin(2x) при x > 0
Вариант 25. xÎ [–1,4;1,9]:
y = ((1+|x|)0,5)/(3+|x|) при x ≤ 0
y = (1+x)/(1+2cos2(x)) при x > 0
Вариант 26. xÎ [–3,5;3,5]:
y = cos(3x)*sin(x) при x ≤ 0
y = cos2(x) – cos(3x) при x > 0
Вариант 27. xÎ[–1,5;1,5]:
y = (1+x2)0,5при x ≤ 0
y = (1+x)/(1+(1+ e0.2x)(1/3)) при x > 0
Вариант 28. xÎ [–3,5;3,5]:
y = 2cos(x)* sin(4x) при x ≤ 0
y = cos3(2x) – cos(x)*sin2(x) при x > 0
Вариант 29. xÎ[–1,8;1,8]:
y = (1 + x)/(1+ 2x2) при x ≤ 0
y = ((2 + x)/(1+x))0,5 при x > 0
Вариант 30. xÎ [–3,5;3,5]:
y = 3sin(2x)*cos(3x) при x ≤ 0
y = sin(x)*cos2(x) при x > 0
П. 1.3. Задания: построить график функции одной переменной с тремя условиями. Использовать условный оператор «если».
Вариант 1. xÎ [–2; 4], шаг 0,5:
y = 3sin(x) cos(4x)прих<–1,5
у = cos(3x) – 4sin(x) при x Î [–1,5; 1]
y = (1 + x)/(1+ 2x3) при х >1
Вариант 2. xÎ [–3,5; 2,5], шаг 0,5:
y = 3sin(x)cos(4x)*sin(4x) прих<–1,5
у = cos(3x) – 4sin(x) при x Î [–1,5; 1]
y = (1 + x)/(1+ 2x3) при х >1
Вариант 3. x Î [–2; 6], шаг 0,5:
y = (0.25+x3)1/3при x < 0
y = 2sin(3x) + cos(x); при x Î [0;3]
y = (1+x)/(1+(1+ e-0.2x)1/3) при x > 3
Вариант 4. xÎ [–2,6; 4,6] шаг 0,5:
y = (1+x)/(2+cos(3x)) при x Î [0,3; 3]
y = ((1+|x|)0,5)/(2+|x|) при x < 0,3
y =e-2x; при x >3
Вариант 5. xÎ [–2; 4], шаг 0,5:
y = (1+4x)/(2+ln(x)) при x>2
y = (1+x2)0,5при x Î [0; 2]
y = sin(x)*cos(x); при x < 0
Вариант 6. xÎ [–6; 6], шаг 0,5:
y = (1 + x)/(1+ x2) при x < 0
y = 1 + ln(x2 + 1) при x Î [0; 3]
y = ((1+2x)/(1+x))0,5 при x > 3
Вариант 7. xÎ [–6; 6], шаг 1:
y = (3 + sin(x))/(1+ x2) при x < 0
y = 2x2cos(2x) при x Î [0; 3]
y = ((1 + 2x2)/(1+ x2))0,5 при x >3
Вариант 8. xÎ [–2,10], шаг 1:
y = 2cos(2*x) при x < 2
y = (1+x)1/3; x Î [2;5]
y = 3x + (1+x2)0,5 при x >5
Вариант 9. xÎ [–2; 6], шаг 0,5:
y = 2sin(3x) при x <0
y = 3sin(x) – cos(2x) при x Î [0;3]
y = (1+|x|)/((x2 + x + 1)1/3) при x > 3
Вариант 10. xÎ [1; 6], шаг 0,5:
y =(tn(3x) –sin(2x)) при x < 3
y = 3(1+x2)0,5при x Î[3;5]
y = 3sin(x) – cos(2x) при x >5
Вариант 11. xÎ [-10; 5], шаг 1:
y =2x3 при x < 0
y = sin(x)*cos(x); при x Î[0;3]
y = ((1+2x)/(1+x))0,5 при x > 3
Вариант 12. x Î [–2; 6], шаг 0,5:
y = e-2x; при x<0
y = 2sin(3x) при x Î[0;3]
y = 3(1+x2)0,5 при x > 3
Вариант 13. xÎ [0; 11], шаг 1:
y = 2sin(3x) + cos(x); при x<3
y = 3sin(x) – cos2(x) при x Î[3;6]
y = (3 + sin(x))/(1+ x2) при x > 6
Вариант 14. xÎ [–4; 5], шаг 0,5:
y = 1 + ln(x2 + 1) при x < 0
y = 3*x + (1+x2)0,5при x Î[0;2]
y = (1+x)/(1+(1+ e-0.2x)1/3) при x > 2
Вариант 15. x Î [–2; 6], шаг 0,5:
y = (1+x2)0,5 при x < 0
y = 2x2cos(2x) при x Î [0;3]
y = (1+|x|)/((x2 + x + 1)1/3) при x >3
Вариант 16. xÎ [–3,5; 3,5], шаг 0,5:
y = (1 + sin(x))/(1+ 2x2) при x < 0
y = 3x3cos(2x) при x Î [0; 2]
y = 2sin(x)* cos(x) прих>2
Вариант 17. xÎ [–3,5; 2], шаг 0,5:
у = sin(3x)*cos(2x) при х<–0,5
y = ((1 + 3x2)/(1+ 2x2))0,5 x Î[–0,5; 1]
y = 3cos(2x) при x > 1
Вариант 18. x Î [–2,5; 2,5], шаг 0,5:
y = sin(2x)*cos(x) – cos2(2x) прих<–1,5
у = 2cos2(x) – 3sin(x) при xÎ [–1,5;1,5]
y = 2x + (3+x2)0,5 при x >1,5
Вариант 19. xÎ [-3,5;3,5], шаг 0,5:
y = 3sin(x) при x < 0
y = 3sin(x) cos(5x)*sin(x) x Î[0; 2]
у = cos2(x) – 2sin(3x) при х>2
Вариант 20. xÎ [–1; 3], шаг 0,5:
y = sin(x) – 3cos(2x) приx< 0
y = 2(1+x3)0,5при x Î[0;2]
y = 2sin(x)* 3cos(x) прих>2
Вариант 21. xÎ [–1,9; 1,9], шаг 0,3:
у = cos2(2x) – sin(x) при x Î [0;1]
y = (1+|x|)/(x2 + 4)1/3 при x < 0
y = 1 + ln(x + 1) при x >1
Вариант 22. xÎ [–3,5; 3,5], шаг 0,5:
y = sin(x)*cos(6x) при x >2
у = cos(2x)*sin(3x) x Î[–2; 2]
y = (2+|x|)0,5/(3+|x|) при х<–2
Вариант 23. xÎ [–1,7; 1,2], шаг 0,1:
y = (1+x)/(5+cos(2x)) при x < 0
y = 3*cos(x)*sin(x) x Î[0; 0,8]
у = cos(2x) – cos(3x) при х >0,8
Вариант 24. xÎ [–1,5; 1,7], шаг 0,1:
y = (3+x2)0,5 при x <-0,5
y = (1+x)/3+(1+ e0.5x)1/3 xÎ[–0,5;0,5]
y = 4cos(3x)*sin(2x) при x > 0,5
Вариант 25. xÎ [–2; 6], шаг 0,5:
у = cos3(x) – cos(2x)*sin(x) при x <1
y = (1 + x)/(1+ 2x3) при x Î [1;3]
y = (2 + x)/(3+x)0,5 при x > 3
Вариант 26. xÎ [–1; 3], шаг 0,5:
y = 3sin(3x)*cos(4x) прих<0
у = sin(4x)*cos2(x) при x Î[0;1,5]
y = 2sin(2x)*cos(2x) прих>1,5
Вариант 27. xÎ [–1,7; 2,7], шаг 0,2:
y = (1 + sin(x)/(1+ 3x2) при x < 0
y = 3x2cos2(3x) при x Î[0; 1,7]
у = sin(3x)*cos2(3x) при x > 1,7
Вариант 28. xÎ [–3,5; 2,5], шаг 0,5:
y = (1 + 2x2)/(3+ 5x2)0,5 при x < -1
y = 2cos2(2x) при x Î [–1; 2]
y = sin(2x)*cos(3x) – cos2(x) прих>2
Вариант 29. xÎ [–2,5; 3,5], шаг 0,5:
y = 4x + (4+x2)0,5 при x < 0
y = 4sin(x) при x Î [0; 2]
у = 2cos(x) – sin2(3x) дляx > 2
Вариант 30. xÎ[–3,5; 2,5], шаг 0,5:
y = 3sin(x) cos(4x)*sin(4x) прих<–1,5
у = cos3(x) – 4sin(x) при x Î[–1,5; 1]
y = (1 + x)/(1+ 2x3) при х >1
П. 1.4. Задания: построить 2 графика в одной системе координат
Вариант 1. xÎ [–3,5;3,5], шаг 0,5:
y= 2cos(4x)*sin(2x)
z= |cox(x)*sin(x) |
Вариант 2. xÎ [–3,5;3,5], шаг 0,5:
y = |sin(4x)*cos(x)|
z = cos(x)*sin(4x)
Вариант 3. xÎ [–4;4], шаг 1:
y = 2sin(x)
z = 3cos(2x)–sin(x)
Вариант 4. xÎ [–4;4], шаг 0,5:
y = 2sin(5x)cos(4x)
z = sin2(x)
Вариант 5. x Î [ – 3,5;3,5], шаг 0,5:
y = 2sin(2 p x)cos(p x)+sin(3 p x);
z = (1 + x)/(1+ 2 x 3) при х >1
Вариант 6. xÎ [–2;2], шаг 0,2:
y = 2sin(x)cos(x);
z = 3cos2(x)sin(x).
Вариант 7. xÎ [–3;4], шаг0,5:
y = 2sin(5x)cos(4x)
z = | cos(x)*sin(x) |
Вариант 8. x Î [ – 3,5;3,5], шаг 0,5:
y = (0,25+ x 3)1/3
y = e -2 x
Вариант 9. xÎ [–2;2], шаг 0,2:
y =tn(3x) –sin(2x)
z = sin(x)*cos(x);
Вариант 10. xÎ [–3,5;3,5], шаг 0,5:
y = 3sin(x) – cos2(x)
z =2x3
Вариант 11. xÎ [–5;5], шаг 0,5:
y = ((1+|x|)0,5)/(2+|x|)
z = 2cos2(x)
Вариант 12. xÎ [–2;2], шаг 0,2:
y = ((1 + 2x2)/(1+ x2))0,5
z = (1+x)/(2+cos3(x))
Вариант 13. xÎ [0,1;3], шаг 0,25:
y = e-2x
z= (1+4x)/(2+ln(x))
Вариант 14. xÎ [–2,5;2,5], шаг 0,5:
y = sin(3x)*cos2(x)
z = 2sin(3x) + cos(x)
Вариант 15. xÎ [0;5], шаг 0,5:
y = (0,25+x3)1/3
z = (1+4x)/(2+ln(x))
Вариант 16. xÎ [0;3,6], шаг 0,3:
y = (1 + 2x2)/(3+ 5x2)0,5
y = 3sin(x)*cos(4x)*sin(4x)
Вариант 17. xÎ [–5;5], шаг 0,5:
y = 2cos2(2x)
z = cos3(x) – 4sin(x)
Вариант 18. xÎ [–2;2], шаг 0,1:
y = sin(2x)*cos(3x) – cos2(x)
z = (1 + x)/(1+ 2x3) прих>1
Вариант 19. xÎ [–2,5;2,5], шаг 0,5:
y = 4x + (4+x2)0,5
z = sin(x)*cos(2x)
Вариант 20. xÎ [0;3], шаг 0,25:
y = cos(3x)*sin(x)
z = cos2(x) – cos(3x)
Вариант 21. xÎ [–3;3], шаг 0,2:
y = 4sin(x)
z = 2cos(x)*sin(x)
Вариант 22. xÎ [–5;5], шаг 0,5:
у = 2cos(x) – sin2(3x)
z = | cos(x)*sin(x) |
Вариант 23. xÎ [–3,5;3,5], шаг 0,5:
y = 3sin(3x)*cos(2x)
z = sin(3x)*cos2(x)
Вариант 24. xÎ [–2;2], шаг 0,2:
y = 2cos2(2x) – 3sin(3x)
z = 2sin(3x)
Вариант 25. xÎ [–2,5;2,5], шаг 0,5:
y= 2cos(4x)*sin(2x)
z = (2+x)1/3
Вариант 26. xÎ [0;3,6], шаг 0,3:
y = 3sin(2x)*cos(3x)
z = sin(x)*cos(2x)
Вариант 27. xÎ [–5;5], шаг 0,5:
y = 2sin(3x) + cos(x);
z = 1 + ln(x2 + 1)
Вариант 28. xÎ [0;3], шаг 0,25:
y = 3x3cos(2x)
z = 3sin(x)
Вариант 29. xÎ [–2,5;2,5], шаг 0,5:
y =tn(3x) –sin(2x)
z = sin(x)*cos(6x)
Вариант 30. xÎ [–2;2], шаг 0,2:
у = cos(2x)*sin(3x)
z = cos(2x) – cos(3x)
П. 1.5. Задания: построить поверхности для x Î [ – 2,2] и y Î [ – 2,2], изменяя значения с шагом 0,5:
Вариант 1. z = x2–2y2
Вариант 2. Z=7x3–6y2
Вариант 3. z=(0,5x–5)2+2(2y–6)2
Вариант 4. z=(0,5x–3)2+(0,5y–3)2
Вариант 5. z=0,5(2x–1)2+0,7(3y–3)2
Вариант 6. z=0,5(2x-5)3+0,5(3y–5)2
Вариант 7. z=(20x–5)2+(4y–5)3
Вариант 8. z=(x-5)2+(y-6)2
Вариант 9. z=3*(x–5)2+3(y–5)2
Вариант 10. z=3(x–5)2+(y–6)2
Вариант 11. z=ex–ey
Вариант 12. z=2х3–3y2
Вариант 13. z = 3x2(y)–5y2
Вариант 14. z = 3x2–2sin2y
Вариант 15. 
где а=2, b =3
Вариант 16. 
Вариант 17. x2+ y2 + z2 = 42 Сфера
Вариант 18. x2/a2 + y2/b2 - z2/c2 = –1 Гиперболоид а=3, b =2, c =1
Вариант 19. x2/a2 + y2/b2 – z2/c2 = 0 Квадратичный конус. а=3, b =2, c =1
Вариант 20. z =x2–6y2
Вариант 21. 
Вариант 22. 
Вариант23. z=3⋅e−(x−2)2−(y−4)
Вариант 24. z =10x2–5y2
Вариант 25. z =sin(x*y)
Вариант 26. 
Вариант 27. z=x2–y2–6
Вариант 28. 
Вариант 29. Z=x3*y–y3*x
Вариант 30. Z=11.83+19.406*x–11.323*y–5.17*x2–4.563*x*y+2.351*y2
П.1.6. Задание: построить график экспериментальной зависимости давления насыщенных паров для каждого вещества от температуры. Задать легенду графика, сделать подписи по осям. построить линию тренда для каждого из графиков, определить ее параметры и поместить на диаграмму величину достоверности аппроксимации R 2. Показать уравнение на диаграмме.
Таблица П.1
