Для нахождения корня методом подбора параметра уравнение следует представить в виде, чтобы правая часть не содержала переменную X.Корень ищется методом последовательных приближений, поэтому предварительно следует установить количество итераций и относительную погрешность («параметры»→«вычисления»). Предельные значения 1000 и 0,00001, соответственно.
Уточняем значения корня для каждого интервала последовательно. На рабочем листе Excelвыбираем ячейки под искомый кореньдля каждого интервала A3, E3, G3, соответственно.Первоначально размещаем в них начальное приближение к корню. Аналогично выбираем ячейкидля функции B3,F3, H3 для которой ищется корень. Причем в полях ссылок указываются абсолютныеадреса ячеек корня и функции.
Теперь переходим непосредственно к нахождению первого корня. В меню выбираем «Данные»→«Анализ»→«Что-если»→«Подбор параметра», после этого появится диалоговое окно «подбор параметра». В полях установки ссылок необходимо ввести ссылку на адрес целевой функции (адрес ячейки, в которой записана функция относительно соответствующего аргумента). Это $B$3 для первого интервала и, соответственно $E$3, $F$3 для двух других. В поле «Значение» вводится значение правой части уравнения. В нашем примере –0 (ноль). В поле «Изменяя значение ячейки» указывается ссылка на ячейку, отведенную под переменную: на первом интервале – $A$3, на втором – $D$3, на третьем – $G$3. Нажимаем кнопку «ОК». На экране появится окно «Результат подбора параметра» с результатами решения. Кроме этого, результат будет и в ячейках, в которых были первоначально введены начальные приближения. Аналогично ищутся и остальные корни.
На рис. 21приведен пример заполнения полей ссылок для первого интервала: указывается абсолютная ссылка на ячейку, выбранную под корень(изменяемое значение ячейки),т.е. $A$3, и адрес ячейки, в которой записана функция $B$3,на рис. 22 – для второго интервала. Результат уточнения корня для первого интервала представлен на рис. 23, готовый результат – на рис. 24.

Рис.21 Пример заполнения ссылок для первого интервала

Рис.22. Пример заполнения ссылок для второго интервала

Рис. 23.Результат уточнения корня для первого интервала
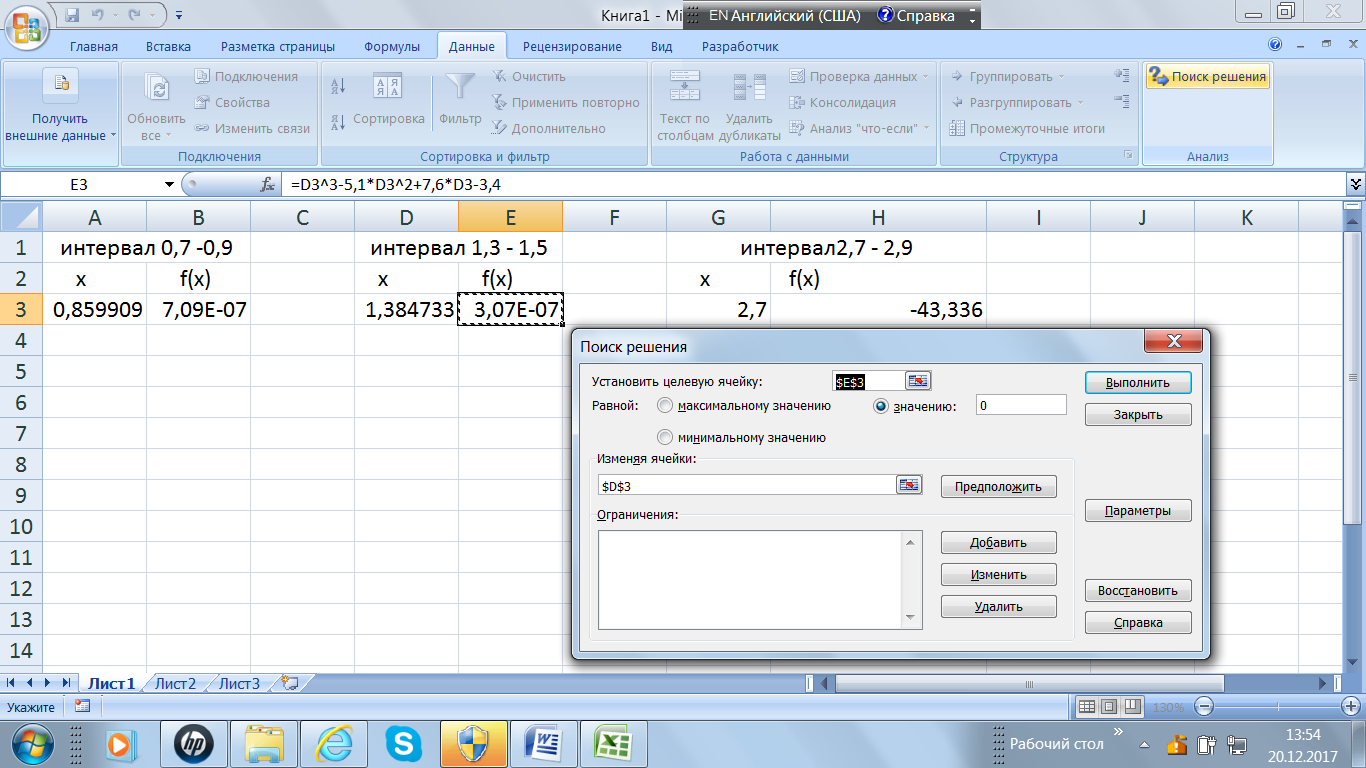
Рис. 24. Метод подбора параметра непосредственно на листе Excel
2.2. Уточнение корня и нахождение экстремума функциис использованием модуля «поиск решения»
Воспользуемся еще одним мощным средством, которое имеется в Excel. Этосредство имеет название Solver (решатель) и позволяет достаточно просто уточнять корни нелинейного уравнения, а также находить минимальные и максимальные значения нелинейной функции. Предварительно необходимо подключить модуль, содержащийSolver. Подключение реализуем по следующему маршруту:«параметры Excel»→«надстройки»→«поиск решения»→«управление»→«перейти» (рис. 25). На панели «надстройки»указать подключение модуля «поиск решения» (рис. 26).
Уточнение корня с использованием модуля «поиск решения» покажем на примере ранее рассмотренной функции f(x)= x3–5,1x2 +7,6x–3,4 (см. раздел 2.3).

Рис. 25.Окно параметров Excel

Рис. 26Подключение надстроек
Для активизации модуля«поиск решения»переходим в главное меню, выбираем«данные»→«поиск решения». В предыдущем разделе поиска корней были определены три отрезка локализации трех корней [0,7 –0,9], [1,3 – 1,5], [2,7– 2,9].На листе Excelвыбираем для уточнения корня на каждом отрезке по две ячейки:E3 (для аргумента), E4 (для функции) – для первого, E6,E7 – для второго; E13,E14 – для третьего,соответственно.В окне «поиск решения» указываем абсолютные адреса ячеек для значений аргумента и функций.На рис. 27, 28показано следующее. Для первогоотрезкаприведен пример заполнения ячеек E3, E4.Для второго подробно показана запись информации в окошко «поиск решения». Для третьего приведено решение: в ячейке E13 – значение корня, в ячейке E14– соответствующее значение функции.

Рис. 27.Поиск решения, уточнение корня

Рис. 28.Поиск решения, рабочее окно
2.3. Уточнение экстремума функции одной переменной с использованием модуля «поиск решения»
Предварительно, как и при нахождении корня, экстремумы необходимо отделить, т.е. найти отрезки, на которых имеется только один экстремум. Исследуемая функция у=х3-1,5х2+7,6х-3,4 (рис. 27) имеет один минимум на отрезке [1,3 – 2,9]и один максимум на [0,7 – 1,3]. Для нахождения точки максимума выбираем опцию «максимальное значение». В качестве целевой ячейки указываем абсолютный адрес ячейки$E$4, в которой записана функция, адрес изменяемой ячейки (координата)-$E$3, далееклик по клавише «выполнить». Результат поиска будет в ячейках E3 иE4, соответственно (рис. 29, 30).Аналогично находятся минимальное значение функции и значение аргумента(координата):

Рис. 29.Поиск экстремума функции
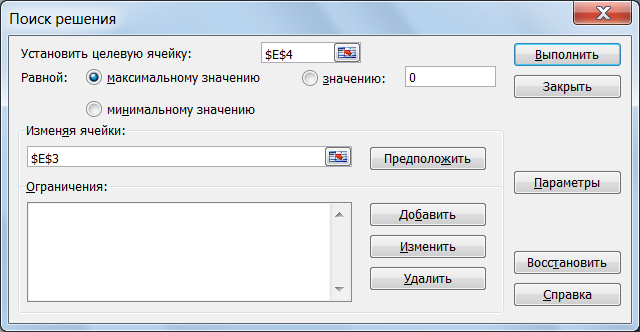
Рис. 30. Окно поискамаксимального значения (модуль«поиск решения»)






