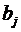Построить двойственную задачу к следующей задаче ЛП.
Прежде чем приступать к построению двойственной задачи, необходимо упорядочить запись исходной: согласовать знаки неравенств в ограничениях с целевой функцией. Так как ЦФ минимизируется, то неравенства должны быть записаны с помощью знака «
». Для этого второе неравенство умножим на -1:
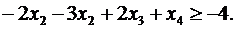
Теперь, вводя двойственные переменные 
, запишем в соответствии с указанным правилом пару двойственных задач:
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
|
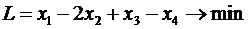
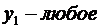
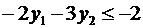
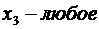
Задача слева – исходная прямая задача, задача справа – двойственная к исходной задаче.
Пример решения пары двойственных задач
Используя теоремы двойственности, решить двойственную задачу, если известно решение прямой задачи.
(12)
Пусть решение задачи найдено одним из стандартных методов: 
. Построим двойственную задачу:
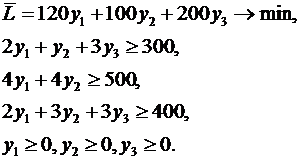(13)
По первой теореме двойственности задача разрешима, причем 
. Найдем оптимальный план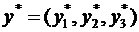 
задачи (13), используя вторую теорему двойственности. Подставим координаты вектора 
в ограничения задачи (12). Получим
Следовательно, в силу УДН, неравенство 
должно выполняться как равенство, т. е.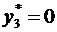 
. Далее так как 
, то в силу УДН,
.
Получаем систему линейных уравнений и решаем ее:
Планы 
и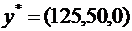 
удовлетворяют УДН, следовательно, в силу второй теоремы двойственности, являются оптимальными в задачах (12) и (13) соответственно.
Пример проверки вектора на оптимальность
Исследовать вектор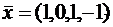 
на оптимальность в задаче ЛП.
Вначале нужно проверить, является ли вектор 
допустимым. Для этого подставляем координаты вектора в ограничения:
Так как второе ограничение выполняется как строгое неравенство, то в силу УДН для оптимальности вектора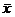 
необходимо выполнение равенства 
.
Построим двойственную задачу:
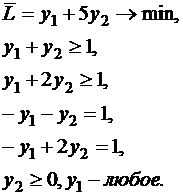
Поскольку , то из третьего и четвертого ограничений получаем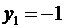 
. Но по УДН из условия 
следует, что должно выполняться равенство в первом ограничении двойственной задачи:
Подставляя значения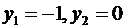 
получим 
Следовательно, УДН не выполняются и вектор 
не является оптимальным в исходной задаче.
Пример решения задачи ЦЛП
Решить задачу ЦЛП.
Решаем задачу ЛП симплекс-методом. Оптимальная таблица имеет вид
| b |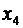 
| 
| |
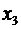
| L | -14/3 | -4/3 | -2/3 |
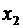
| 5/3 | 1/3 | 2/3 |
| 4/3 | 2/3 | -2/3 |
Оптимальное решение 
не является целочисленным. Выберем среди нецелочисленных переменных 
переменную 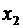с максимальной дробной частью и построим соответствующее отсечение:
Приписывая это ограничение к симплексной таблице и проводя стандартное преобразование двойственным симплекс-методом, получим:
| b |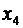
|
| |
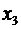
| L | -14/3 | -4/3 | -2/3 |
|
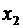
| 5/3 | 1/3 | 2/3 |
|
| 4/3 | 2/3 | -2/3 |
| -2/3 | -1/3 | -2/3 |
| b |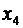
|
| |
| L | -4 | -1 | -1 |
|
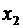
| 1 | 0 | 1 |
|
| 2 | 1 | -1 |
|
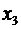
| 1 | 1/2 | -3/2 |
Полученная таблица является оптимальной. Соответствующее оптимальное решение 
является целочисленным. Значение функции на этом решении 
.
Пример построения опорного плана методом
северо-западного угла
|
| 1 | 2 | 3 |
| ||||||||
| 1 | 15 | 20 | 35 | 20 | 0 | 0 | ||||||
| 2 |
| 0 | 30 | 30 | 30 | 30 | ||||||
|
| 15 | 20 | 30 | = | ||||||||
| 0 | 20 | 30 | ||||||||||
| 0 | 0 | 30 | ||||||||||
| 0 | 0 | 0 | ||||||||||
В таблице, обведенной снизу и справа двойной чертой, указаны объемы перевозок, полученные методом северо-западного угла. При этом небазисные нулевые перевозки не проставлены. Справа и внизу таблицы содержатся объемы возможных запасов и спросов. В число базисных перевозок вошла перевозка 
, так как на предыдущем шаге 
и по п.3 метода считается выбывшим только поставщик, а неудовлетворенный спрос второго потребителя равен 
.
Пример построения опорного плана методом
минимальной стоимости
|
| 1 | 2 | 3 |
| |||||||||
| 1 | 9 | 57 | 301 | 35 | 5 | 5 | 5 | ||||||
| 2 | 152 | 153 | 8 | 30 | 30 | 15 | 0 | ||||||
|
| 15 | 20 | 30 | = | |||||||||
| 15 | 20 | 0 | |||||||||||
| 0 | 20 | 0 | |||||||||||
| 0 | 5 | 0 | |||||||||||
