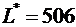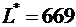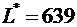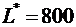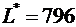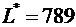Пример решения транспортной задачи методом

потенциалов

	1	2	3
1	³	⁸	²	35
2	⁷	⁴	⁸	30
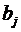
	15	20	30	=

Опорный план этой задачи найден методом северо-западного угла.

Приписываем к таблице строку для платежей 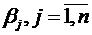и столбец для платежей . Псевдостоимости записываем в левом углу клетки, а стоимости – в правом.

Из условий в базисных клетках получаем систему уравнений:

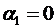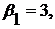
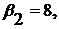
Полагая , находим последовательно платежи и псевдостоимости для свободных клеток. Получаем таб-лицу

	1	2	3
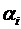
1	3 15	8 [-] 20	12 2 [+]	35	0
2	-1 7	4 [+] 0	8 [-] 30	30	-4
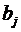
	15	20	30	=
	3	8	12

Стоимость перевозок по плану этой таблицы

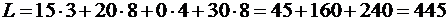Так как клетка (1,3) имеет отрицательную цену , то план не является оптимальным. Строим для клетки (1,3) цикл. Цена цикла . По циклу переносим 20 единиц груза (больше нельзя, чтобы перевозки в клетке (1,2) не стали отрицательными). При этом стоимость плана изменяется на . Для нового плана вычисляем новые значения платежей и псевдостоимостей:

	1	2	3
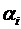
1	3 [-] 15	-2 8	2 [+] 20	35	0
2	9 7 [+]	4 20	8 [-] 10	30	6
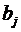
	15	20	30	=
	3	-2	2

Стоимость перевозок по плану этой таблицы

Полученная таблица имеет клетку (2,1) с отрицательной ценой . По циклу этой клетки переносим 10 единиц груза, при этом стоимость плана уменьшается на единиц, и получаем новый опорный план с новой системой платежей и псевдостоимостей:

	1	2	3
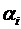
1	3 5	0 8	2 30	35	0
2	7 10	4 20	5 8	30	4
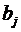
	15	20	30	=
	3	0	2

Стоимость перевозок по плану этой таблицы Так как в последней таблице все псевдостоимости не превосходят соответствующих стоимостей, то полученный опорный план является оптимальным. Стоимость перевозок при этом

ЗАДАНИЯ ДЛЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ

Привести задачу ЛП к канонической форме

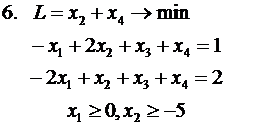
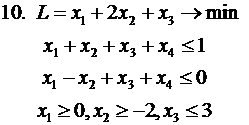
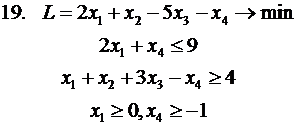
Решить задачу ЛП графически

(во всех заданиях )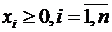

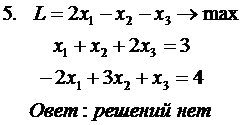
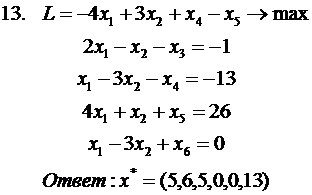
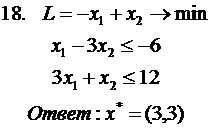
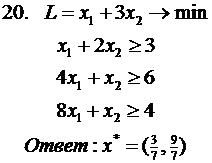
Определить допустимое базисное решение методом

искусственного базиса (во всех заданиях )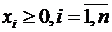

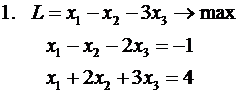
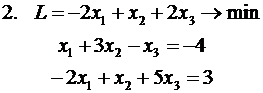
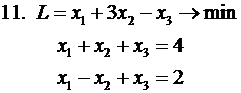
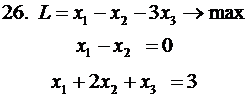
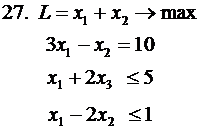
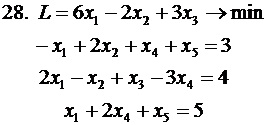
Решить задачу ЛП симплекс-методом

(во всех заданиях )

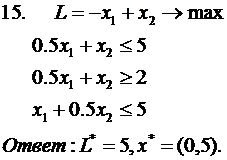
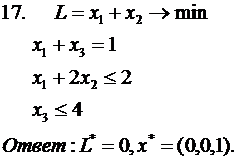
Решить задачу ЛП двойственным симплекс-методом

(во всех заданиях )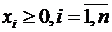

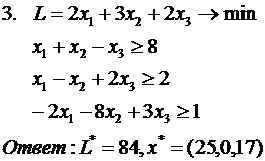
Определить задачу, двойственную к исходной

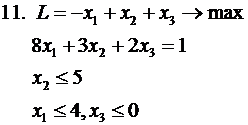
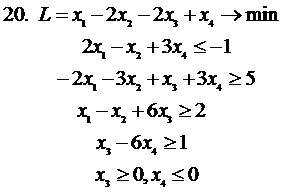
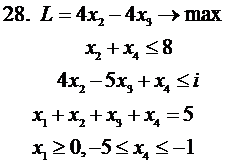
2.7. Используя теоремы двойственности, решить исходную
и двойственную задачи (во всех заданиях )

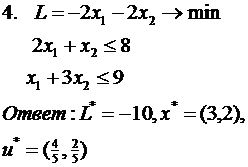
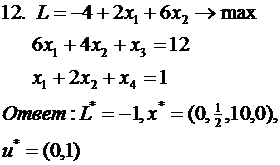
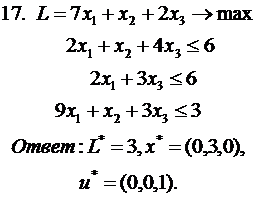
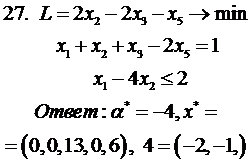
Проверить вектор на оптимальность

(во всех заданиях )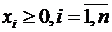

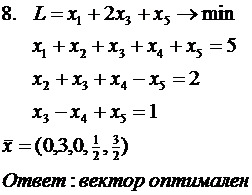
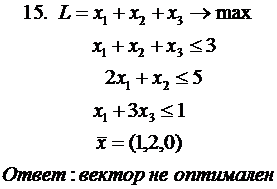
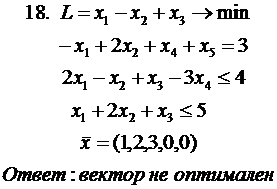
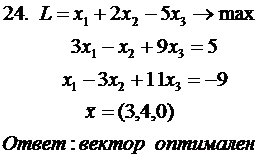
Решить задачу ЦЛП методом Гомори

(во всех заданиях )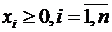

Решить транспортную задачу методом потенциалов

1.						2.
12	6	29	19	21	13	4	21	12	8	1	21
14	3	30	10	10	27	20	8	25	15	23	21
15	27	28	11	24	16	17	1	11	5	3	23
1	23	26	15	13	14	23	10	24	6	5	23
14	14	14	14	14		22	22	22	11	11

3.						4.
5	3	24	10	25	24	21	19	11	12	12	24
30	2	22	16	7	15	26	29	14	1	26	12
30	24	27	29	10	16	39	1	22	8	25	18
15	17	21	2	3	24	53	20	40	26	28	16
12	13	15	15	24		11	13	26	10	10

5.						6.
25	28	20	15	7	16	14	25	18	19	23	33
27	5	11	23	10	12	2	17	16	24	2	25
1	25	14	16	16	14	29	3	7	15	22	25
8	6	4	16	18	18	5	20	17	23	10	17
7	8	4	11	30		33	11	11	11	34


7.						8.
8	1	19	1	15	18	6	6	5	7	17	16
8	27	30	7	7	23	15	8	9	6	23	10
10	20	19	26	20	17	3	14	19	4	20	24
18	28	25	7	22	22	16	13	11	12	2	60
21	21	9	9	20		29	5	35	31	10

9.						10.
11	10	15	8	7	16	0	11	2	4	6	15
12	14	29	20	20	15	1	8	7	5	13	9
18	7	5	25	27	24	14	6	9	3	5	11
24	4	30	24	26	15	10	14	16	15	17	25
15	15	15	15	10		10	5	4	21	20

11.						12.
3	18	22	7	1	35	5	13	1	2	6	40
15	2	24	20	4	40	28	3	30	12	30	35
27	3	7	5	11	15	1	8	22	20	27	25
12	28	8	30	31	25	4	17	15	24	19	10
32	28	14	16	25		20	12	18	50	10

1 3.						1 4.
6	1	8	14	5	10	3	2	22	5	13	23
19	27	3	8	18	4	15	1	21	8	4	20
9	2	4	6	5	12	15	12	24	25	5	26
11	6	9	12	29	8	8	9	20	1	2	16
6	9	5	5	9		15	10	18	30	12

15.						16.
1	3	3	1	2	10	29	1	2	1	19	30
10	4	8	3	11	20	28	31	8	30	10	10
20	6	9	1	8	30	15	4	10	20	21	45
4	20	10	17	6	40	25	28	16	5	22	15
15	25	10	20	30		10	15	35	30	20

17.						18.
5	1	8	13	3	15	8	6	10	20	3	15
4	8	1	2	6	8	7	1	8	11	9	15
10	20	24	15	16	21	3	4	5	17	21	15
18	17	12	7	6	19	8	9	14	23	16	10
11	9	10	13	20		13	27	5	7	3

19.						20.
17	10	21	11	8	24	3	5	30	18	22	16
24	13	10	10	19	20	13	4	29	11	9	10
9	12	27	16	20	11	14	28	27	12	23	24
9	4	4	10	11	11	2	22	27	14	14	60
21	12	10	14	9		29	5	35	31	10

21.						22.
7	2	3	11	20	20	2	4	3	8	1	24
4	8	13	15	6	20	19	18	10	7	5	16
3	7	10	20	31	20	14	12	20	6	11	15
13	14	8	10	11	22	13	7	17	16	21	24
22	10	16	14	20		24	15	15	13	12

23.						24.
7	15	6	19	17	6	3	1	2	4	3	10
14	8	17	3	9	26	1	2	4	5	6	5
5	13	11	4	22	20	7	9	12	3	5	5
27	28	1	20	5	23	10	12	8	11	10	10
12	30	18	10	15		10	5	5	5	5

25.						26.
2	4	1	3	6	35	5	3	8	49	32	80
7	9	8	11	7	10	28	4	14	27	7	10
4	1	2	5	6	18	81	15	16	10	25	40
5	3	9	7	8	17	30	9	20	64	2	20
15	3	30	12	20		15	70	17	5	43

27.						28.
6	6	3	7	17	16	12	6	28	19	21	14
15	8	9	6	23	10	14	3	30	10	10	16
3	14	19	4	20	24	15	27	28	11	24	27
16	13	11	12	2	60	1	23	26	15	13	13
29	5	35	31	10		14	14	14	14	14

29.						30.
1	19	4	15	6	19	10	2	4	1	11	3
22	8	14	3	21	21	3	12	13	2	8	16
5	30	11	12	7	8	1	8	3	4	7	7
6	17	24	23	9	15	2	7	5	3	20	13
20	13	10	9	11		4	14	5	14	2

<== предыдущая лекция	\|	следующая лекция ==>
Пример построения двойственной задачи	\|	Оргкомитет оставляет за собой право вносить изменения в настоящее Положение.

Поделиться с друзьями:

Дата добавления: 2018-10-14; Мы поможем в написании ваших работ!; просмотров: 232 | Нарушение авторских прав

Поиск на сайте:

Лучшие изречения:

2533 -

| 2390 -