Симплекс-метод применяется для решения задач ЛП, представленных в специальной форме:
(16)
Характерная особенность задачи (16) – известное базисное допустимое решение
Чтобы применить симплекс-метод для решения задачи ЛП в произвольной форме, необходимо привести эту задачу к виду (16), т. е. выделить начальное допустимое базисное решение. Для этого в симплекс-метод вводят подготовительный этап. Один из методов для реализации подготовительного этапа называется методом искусственного базиса и состоит в следующем [1,2,3].
Вычислительная схема метода искусственного базиса
Шаг 1. Приводим задачу ЛП к канонической форме с неотрицательными правыми частями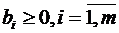 
:
(17)
Шаг 2. В каждую i -ю строку ограничений (17) вводим искусственную неотрицательную переменную 
и строим вспомогательную задачу ЛП вида:
(18)
В задаче (18) 
– допустимое базисное решение, и задача (18) легко может быть сведена к виду (16). Для этого целевую функцию необходимо выразить через свободные переменные 
:
Шаг 3. Для вспомогательной задачи (18) строим симплексную таблицу
| b | 
| … | 
| |
| 
| 
| … | 
|
| 
| 
| … | 
|
| … | … | …………………. | ||
| 
| 
| … | 
|
и находим оптимальное решение вспомогательной задачи с помощью симплекс-метода.
Шаг 4. Если 
и все переменные 
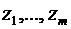являются небазисными, то m переменных из 
войдут в базис и система ограничений, соответствующих симплексной таблице, будет иметь вид
(19)
Так как переменные 
, то их исключили из системы (19), не нарушив при этом равенств. Выражая целевую функцию основной задачи 
через небазисные переменные 
системы (19), получим исходную задачу (17) в виде (16).
Шаг 5. Если , но в базисе остались искусственные переменные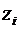 
, для которых 
(вырожденный случай), то проводим для каждой искусственной переменной 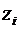из базиса следующее преобразование симплексной таблицы.
Выбираем ведущим столбцом столбец такой переменной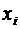 
, для которой элемент индексной строки 
, а элемент столбца 
. В этом случае строка искусственной переменной 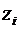будет ведущей и после стандартного преобразования симплексной таблицы (шаг 6 из прямого симплекс-метода) искусственная переменная 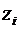выведется из базиса. В результате получим симплексную таблицу, соответствующую шагу 4.
Шаг 6. Если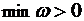 
, то допустимого решения в исходной задаче (17) не существует (не могут все искусственные переменные 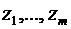быть равными нулю в задаче (18), а значит система ограничений задачи (17) несовместна) – процесс решения исходной задачи (17) завершается.
Пример решения задачи методом искусственного базиса
Выделить допустимое базисное решение для задачи ЛП:
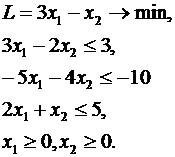
Приведем задачу к канонической форме на минимум с неотрицательными правыми частями:
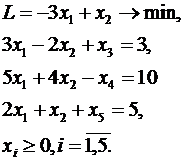
Заметим, что переменные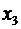 
и 
можно использовать для введения в исходный базис, поэтому в первую и третью строку ограничений можно не вводить искусственные переменные.
Во вторую строку ограничений вводим искусственную переменную z, потому что в этой строке нет переменной, которую можно взять базисной, не проводя при этом дополнительных преобразований всей системы ограничений.
Полученная вспомогательная задача имеет вид
Приведем задачу к виду (16):
Выпишем соответствующую симплексную таблицу:
| B | 
| 
| 
| |
| 10 | 5 | 4 | -1 |
| 3 | 3 | -2 | 0 |
| 10 | 5 | 4 | -1 |
| 5 | 2 | 1 | 0 |
Ведущий столбец рекомендуется выбирать не по максимальному положительному элементу строки целевой функции, а так, чтобы из базиса выводилась искусственная базисная переменная (соответствующая ведущая строка должна быть строкой искусственной переменной). Так, выбрав ведущим столбцом столбец переменной 
, получим ведущую строку – строку с переменной z (выбирая ведущим столбцом 
, получили бы ведущую строку 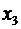, и из базиса выводилась бы переменная ).
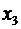Итак, искусственная переменная z выйдет из базиса, а переменная введется в базис.
Симплексная таблица преобразуется к виду:
| B |
|
|
| |
|
| 0 | 0 | -1 | 0 |
|
| 8 | 11/2 | 1/2 | -1/2 |
|
| 5/2 | 5/4 | 1/4 | -1/4 |
|
| 5/2 | 3/4 | -1/4 | 1/4 |
Так как значение 
, то полученный базис 
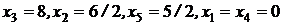является начальным допустимым базисом для исходной задачи ЛП. Чтобы выразить целевую функцию 
через небазисные переменные 
, подставим значение базисной переменной 
в целевую функцию. В результате получим:
Тогда исходная задача будет иметь вид специальной формы задачи ЛП:
что и требовалось получить в результате решения вспомогательной задачи.
