Метод работает с теми же симплексными таблицами, что и прямой симплекс-метод для задачи на минимум. Сначала определяется переменная, подлежащая выводу из базиса, а затем переменная, вводимая в базис [1,3].
Вычислительная схема двойственного симплекс-метода
Шаг 0. Начинаем с симплексной таблицы, где 
.
| B |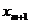 
| … | 
| |
| L | 
| 
| … | 
|
| 
| 
| … | 
|
| … | … | ………….. | ||
| 
| 
| … | 
|
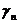
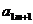
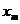
Шаг 1. Проверка на оптимальность. Если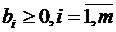 
, то решение 
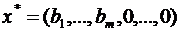– оптимальное.
Шаг 2. Выбор ведущей строки. Выбираем среди номеров i, для которых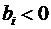 
, номер k с максимальным по модулю значением
.
Строка k объявляется ведущей.
Шаг 3. Проверка на неразрешимость. Если в строке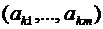 
нет отрицательных элементов, то двойственная целевая функция неограниченная и, следовательно, прямая задача не имеет допустимых решений. Процесс решения завершается.
Шаг 4. Выбор ведущего столбца s. Выбираем среди отрицательных элементов строки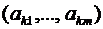 
элемент с номером s, для которого выполняется равенство
.
Столбец s объявляется ведущим, а элемент 
– ведущим элементом.
Шаг 5. Проводим стандартное преобразование симплексной таблицы (Шаг 6 из прямого симплекс-метода).
Пример решения задачи двойственным симплекс-методом
Решить задачу ЛП двойственным симплекс-методом:
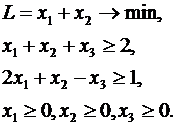
Приводим задачу к каноническому виду:
Знаки в ограничениях заменили противоположными для того, чтобы переменные 
и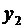 
можно было взять в качестве базисных. Симплексная таблица имеет вид
| b | 
| 
| 
| |
| L | 0 | -1 | -1 | 0 |
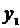
| -2 | -1 | 1 | -1 |
| -1 | -2 | -1 | 1 |
Таблица двойственно-допустимая, но не оптимальная. Выбираем ведущую строку – это строка переменной , ведущий столбец – это столбец переменной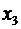 
. После преобразования таблица принимает вид
| b |
|
|
| |
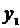
| L | 0 | -1 | -1 | 0 |
|
| 2 | 1 | -1 | -1 |
|
| -3 | -3 | 0 | 1 |
Так как в столбце b есть отрицательная переменная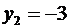 
, то эту строку выбираем ведущей, а столбец переменной 
будет ведущим столбцом. После преобразования получаем таблицу:
| b |
|
|
| |
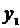
| L | 1 | -1/3 | -1 | -1/3 |
|
| 1 | 1/3 | -1 | -2/3 |
|
| 1 | -1/3 | 0 | -1/3 |
которая является оптимальной. Соответствующее оптимальное решение имеет вид 
.
Двойственность в ЛП
Постановка задачи
Рассмотрим пару задач ЛП вида:
(I) (II)
… …
… …
… …
… …
.
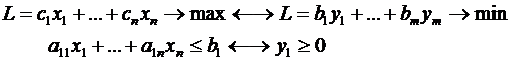
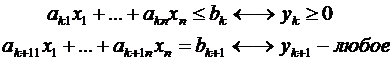
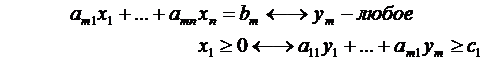
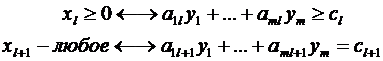
Задачу (I) называют прямой задачей ЛП, а (II) – двойственной. Неравенства задач (I) и (II), соответствующие друг другу (по стрелке), называются сопряженными. Заметим, что задача двойственная к (II), есть исходная прямая задача, т. е. соотношение двойственности взаимное. Поэтому можно из такой пары задач любую считать прямой, а другую – двойственной.
