 Выберем на плоскости декартову прямоугольную систему координат
Выберем на плоскости декартову прямоугольную систему координат  (рис. А.10). Около начала координат
(рис. А.10). Около начала координат 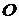 , опишем окружность единичного радиуса (единичную окружность). Зададим произвольное число
, опишем окружность единичного радиуса (единичную окружность). Зададим произвольное число  . Рассмотрим вектор
. Рассмотрим вектор  с началом в точке
с началом в точке 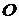 и концом в точке
и концом в точке  , принадлежащим пересечению единичной окружности с осью абсцисс. Повернем его на угол
, принадлежащим пересечению единичной окружности с осью абсцисс. Повернем его на угол  радиан, получив в результате вектор
радиан, получив в результате вектор  . Это означает, что конец вектора «пройдет» на единичной окружности дугу
. Это означает, что конец вектора «пройдет» на единичной окружности дугу 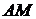 длины
длины  (
( ) в направлении против (по) часовой стрелке при
) в направлении против (по) часовой стрелке при  (
( ). Функция синус (косинус) ставит в соответствие числу
). Функция синус (косинус) ставит в соответствие числу  ординату
ординату 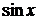 (абсциссу
(абсциссу 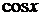 ) точки
) точки  .
.
В тригонометрии используются также функции тангенс, котангенс, секанс и косеканс, определяемые соответственно равенствами:
 ,
,  ,
,  и
и 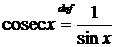 .
.
Свойства тригонометрических функций:
1) области определения 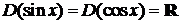 ,
,  ,
, 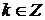 ,
,  ,
,  ;
;
2) области значений  ,
,  ;
;
3) косинус – четная функция, а синус, тангенс и котангенс – нечетные функции;
4) синус и косинус – функции, периодические с периодом  , а тангенс и котангенс – функции, периодические с периодом
, а тангенс и котангенс – функции, периодические с периодом 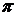 ;
;
 5) синус возрастает на промежутках
5) синус возрастает на промежутках  и убывает на промежутках
и убывает на промежутках  ,
,  ;
;
 |
косинус возрастает на промежутках
 и убывает на промежутках
и убывает на промежутках  ,
,  ;
;
тангенс возрастает на промежутках  ,
,  ;
;

 |
котангенс убывает на промежутках
 ,
,  ;
;
6) основные тождества, связывающие тригонометрические функции:
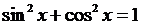 ,
,  ,
,  ,
,  ,
,
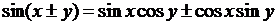 ,
, 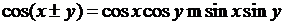 ,
,
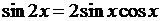 ,
, 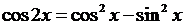 .
.
Графики тригонометрических функций изображены на рис. A.11-A.14.
Обратные тригонометрические функции
 Функция
Функция  ,
,  , возрастает и имеет областью значений отрезок
, возрастает и имеет областью значений отрезок 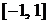 . Поэтому она имеет обратную функцию, которая определена на
. Поэтому она имеет обратную функцию, которая определена на  , обозначается
, обозначается  иназывается арксинусом.
иназывается арксинусом.
 Функция
Функция  ,
,  убывает и имеет областью значений отрезок
убывает и имеет областью значений отрезок  . Поэтому она имеет обратную функцию, которая определена на
. Поэтому она имеет обратную функцию, которая определена на  , обозначается
, обозначается  иназывается арккосинусом.
иназывается арккосинусом.
Функция  ,
,  , возрастает и имеет областью значений множество действительных чисел. Поэтому у нее есть обратная функция, которая определена на
, возрастает и имеет областью значений множество действительных чисел. Поэтому у нее есть обратная функция, которая определена на 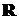 , обозначается
, обозначается  иназывается арктангенсом.
иназывается арктангенсом.


Функция  ,
,  , убывает и имеет областью значений множество действительных чисел. Поэтому у нее есть обратная функция, которая определена на
, убывает и имеет областью значений множество действительных чисел. Поэтому у нее есть обратная функция, которая определена на 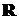 , обозначается
, обозначается  иназывается арккотангенсом.
иназывается арккотангенсом.
Свойства обратных тригонометрических функций.
1) Области определения:

 ,
,  .
.
2) Множества значений:

 ,
,

 .
.
3)  ,
,  ,
,  .
.
4) Арксинус и арктангенс – возрастающие функции, а арккосинус и арккотангенс – убывающие.
5) Арксинус и арктангенс являются нечетными функциями, а арккосинус и арккотангенс не являются ни четными, ни нечетными.
6) 
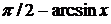 ,
, 
 .
.
Графики обратных тригонометрических функций представлены на рис. A.15-A.18.
Гиперболические функции
Гиперболическим синусом называется функция
 .
.
Гиперболическим косинусом называется функция
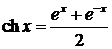 .
.
Определим также гиперболический тангенс
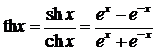
и гиперболический котангенс
 .
.
Свойства гиперболических функций:
1) области определения 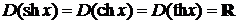 ,
, 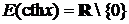 ;
;
2) области значений
 ,
,  ,
,  ,
,  ;
;
3) функции  ,
,  являются возрастающими,
являются возрастающими,  убывает на
убывает на  и возрастает на
и возрастает на  ,
,  убывает на
убывает на  и на
и на 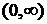 ;
;
4) функции  ,
,  и
и  являются нечетными, а
являются нечетными, а  – четной;
– четной;
5) справедливо основное гиперболическое тождество  и тождества, подобные тождествам для тригонометрических функций:
и тождества, подобные тождествам для тригонометрических функций:
 ;
; 
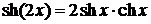 ;
; 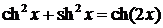 ;
;
 .
.
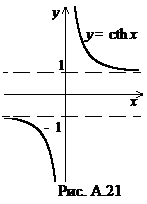
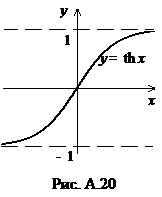
Графики гиперболических функций представлены на рис. A.19-A.21.
 | |||||
 | |||||
 | |||||






