6.3.1. Докажите непрерывность функций  , используя определение.
, используя определение.
Исследовать функции на непрерывность и выяснить характер точек разрыва (если они есть).
6.3.2. 
| 6.3.3. 
|
6.3.4. 
| 6.3.5. 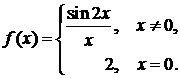
|
6.3.6. 
| 6.3.7. 
|
6.3.8. 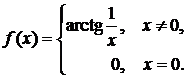
| 6.3.9. 
|
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Дифференциальное исчисление функций одной переменной: метод. указания / сост.: В.Ш. Ройтенберг, Л.А. Сидорова, С.А. Кривелевич, О.Н. Колесников. – Ярославль: Изд-во ЯГТУ, 2007. – 39 с. – № 2688.
2. Пискунов, Н.С. Дифференциальное и интегральное исчисления: учебник для втузов: в 2 т. – М.: Интеграл-Пресс, 2001.
3. Бугров, Я.С. Дифференциальное и интегральное исчисление / Я.С. Бугров, С.М. Никольский. – М.: Наука, 1980. – 342 с.
4. Кудрявцев, Л.Д. Курс математического анализа. Т.1. – М.: Высш. шк., 1981. – 250 с.
5. Сборник задач по математике для втузов. Линейная алгебра и основы математического анализа / под редакцией А.В. Ефимова и В.П. Демидовича. – М.: Наука, 1981. – 462 с.
6. Фихтенгольц, Г.М. Курс дифференциального и интегрального исчисления. Т. 1. – М.: Наука, 1970. – 608 с.
7. Данко, П.Е. Высшая математика в упражнениях и задачах: в 2 ч.: Учеб. пособие для втузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - М.: Высш. шк., 1999.
Ответы
1.3.1. а)  ; б)
; б) 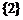 . 1.3.2.
. 1.3.2.  ;
; 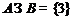 ;
;  ;
;  .
.
1.3.3. б)  ;
;  ;
;  ,
,  - не существует.
- не существует.
| 1.3.5. истинно. | 1.3.6. ложно. | 1.3.7. истинно. | 1.3.8. ложно. | 1.3.9. истинно. |
| 1.3.10. ложно. | 1.3.11. истинно. | 1.3.12. истинно. | 1.3.13. истинно. | 1.3.14. истинно. |
2.3.2.  . 2.3.4.
. 2.3.4.  . 2.3.6.
. 2.3.6.  ;
;  ;
;  ;
;  . 2.3.8. б)
. 2.3.8. б) 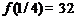 ,
,  ,
,  .
.
2.3.10.  ,
, 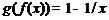 . 2.3.11.
. 2.3.11.  . 2.3.12.
. 2.3.12.  .
.
2.3.14. параболу  сдвигаем вправо на 3/2 и вниз на 9/4.
сдвигаем вправо на 3/2 и вниз на 9/4.
2.3.16. График 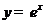 сжимаем в 2 раза вдоль оси O x и сдвигаем вверх на 1.
сжимаем в 2 раза вдоль оси O x и сдвигаем вверх на 1.
2.3.18. График 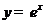 симметрично отражаем относительно оси O x и оси O y и сдвигаем вверх на 1.
симметрично отражаем относительно оси O x и оси O y и сдвигаем вверх на 1.
2.3.20. График  сдвигаем вниз на 1; часть графика, расположенную ниже оси O x, симметрично отражаем относительно оси O x.
сдвигаем вниз на 1; часть графика, расположенную ниже оси O x, симметрично отражаем относительно оси O x.
2.3.22. часть графика 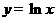 , расположенную ниже оси O x, симметрично отражаем относительно оси O x, а затем сдвигаем вниз на 1.
, расположенную ниже оси O x, симметрично отражаем относительно оси O x, а затем сдвигаем вниз на 1.
2.3.24. Гиперболу 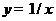 сдвигаем вправо на 1 и вверх на 1.
сдвигаем вправо на 1 и вверх на 1.
2.3.26. Синусоиду  сдвигаем влево на
сдвигаем влево на  ; сжимаем в 2 раза вдоль оси O x и растягиваем в 3 раза вдоль оси O y.
; сжимаем в 2 раза вдоль оси O x и растягиваем в 3 раза вдоль оси O y.
2.3.28. График 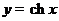 симметрично отражаем относительно оси O x и сдвигаем вверх на 2.
симметрично отражаем относительно оси O x и сдвигаем вверх на 2.
2.3.30. График  симметрично отражаем относительно оси O y и сдвигаем вправо на 4.
симметрично отражаем относительно оси O y и сдвигаем вправо на 4.
2.3.32. При 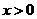
 ; при
; при  строим вторую ветвь симметрично первой относительно оси O y; обе ветви симметрично отражаем относительно оси O x.
строим вторую ветвь симметрично первой относительно оси O y; обе ветви симметрично отражаем относительно оси O x.
2.3.34. График  растягиваем в 2 раза вдоль оси O y и сдвигаем вверх на
растягиваем в 2 раза вдоль оси O y и сдвигаем вверх на  .
.
| 3.3.3. 1. | 3.3.4. 2/3. | 3.3.5. 1. | 3.3.6. 2. |
| 3.3.7. 2. | 3.3.8. 0. | 3.3.9. 1. | 3.3.10. 1. |
| 4.3.2. -9. | 4.3.3. 2,5. | 4.3.4. ∞. | 4.3.5. ∞. |
| 4.3.6. 0. | 4.3.7. 0. | 4.3.8. 7/6. | 4.3.9. ∞. |
| 4.3.10. ¾. | 4.3.11. 2. | 4.3.12. 4. | 4.3.13. 1/32. |
| 4.3.14. 5. | 4.3.15. 3 | 4.3.16. ∞. | 4.3.17. 0. |
| 4.3.18. 0. | 4.3.19. 0. | 4.3.20. 0. | 4.3.21. 1/3. |
| 4.3.22. 0. | 4.3.23. 3/2. | 4.3.24. 2. | 4.3.25. α/β. |
| 4.3.26. ½. | 4.3.27. ½ | 4.3.28. 0. | 4.3.29. 0. |
| 4.3.30. 1 | 4.3.31. exp(-3/2). | 4.3.32. e. | 4.3.33.  . .
|
| 4.3.34. exp(-6). | 4.3.35. 2. | 4.3.36. exp(-1). | 4.3.37. e. |
5.3.2.  . .
| 5.3.3. 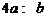 . .
| 5.3.4.  . .
| 5.3.5.  . .
|
5.3.6.  . .
| 5.3.7.  . .
| 5.3.8. 2. | 5.3.9. ∞. |
| 5.3.10. 1/6. | 5.3.11. 1/3. | 5.3.12. -19/3. | 5.3.13. 1. |
5.3.14. 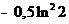 . .
| 5.3.15. 2/5. | 5.3.16.  . .
| 5.3.17. 2. |
| 5.3.18. 3. | 5.3.19. -4. | 5.3.20. 4/3. | 5.3.21. 3/2. |
| 5.3.22. 0. | 5.3.23. 0. | 5.3.24. 1. | 5.3.25. 0. |
| 5.3.26. 0. | 5.3.27. 1. | 5.3.28.  . .
| 5.3.29.  . .
|
| 5.3.30. exp(-2). | 5.3.31. e. | 5.3.32. 0. | 5.3.33. +∞. |
6.3.2.  - точка разрыва 2 рода. - точка разрыва 2 рода.
| 6.3.3.  - точка разрыва 2 рода. - точка разрыва 2 рода.
| 6.3.4.  - точка разрыва 1 рода. - точка разрыва 1 рода.
| 6.3.5.  непрерывна на непрерывна на 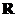 . .
|
6.3.6.  непрерывна на непрерывна на 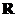 . .
| 6.3.7.  - точка разрыва 1 рода. - точка разрыва 1 рода.
| 6.3.8.  - точка разрыва 1 рода. - точка разрыва 1 рода.
| 6.3.9.  непрерывна на непрерывна на 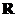 . .
|
Приложение А
ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ.
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ


Постоянная функция
 Это функция
Это функция  , которая ставит в соответствие любому
, которая ставит в соответствие любому  число
число  (рис. А.1).
(рис. А.1).
Степенная функция
Степенная функция  с показателем
с показателем  определяется следующим образом.
определяется следующим образом.
· При натуральном показателе  :
:  ,
,  , и
, и  ,
,  , для
, для  .
.
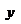
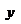
 При нечетном n область значений функции –
При нечетном n область значений функции – 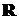 , функция нечетная и возрастающая, ее график изображен на рис. A.2. При четном n область значений – промежуток
, функция нечетная и возрастающая, ее график изображен на рис. A.2. При четном n область значений – промежуток  , функция четная, убывает на промежутке
, функция четная, убывает на промежутке  и возрастает на промежутке
и возрастает на промежутке  , ее график изображен на рис. A.3.
, ее график изображен на рис. A.3.
· 
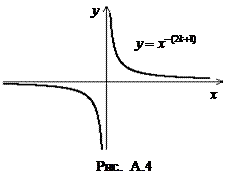 При целом отрицательном показателе
При целом отрицательном показателе  :
:
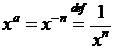 ,
,  .
.
При нечетном n область значений –  , функция нечетная, возрастающая на промежутках
, функция нечетная, возрастающая на промежутках  и
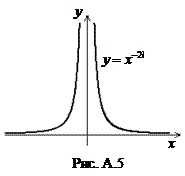
и  , ее график изображен на рис. A.4. При четном n область значений – промежуток
, ее график изображен на рис. A.4. При четном n область значений – промежуток 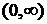 , функция четная, возрастает на промежутке
, функция четная, возрастает на промежутке  , убывает на промежутке
, убывает на промежутке 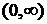 , ее график изображен на рис. A.5.
, ее график изображен на рис. A.5.
· При положительном рациональном показателе 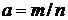
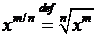 ,
,  .
.
· При отрицательном рациональном показателе 
 ,
,  .
.
· При иррациональном показателе  для любого
для любого  существует единственное число
существует единственное число  такое, что для любых рациональных чисел
такое, что для любых рациональных чисел  и
и  , удовлетворяющих условию
, удовлетворяющих условию 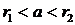 ,
,  . Полагают
. Полагают  .
.
 |  | ||
Степенная функция с нецелым показателем
 возрастает при
возрастает при  и убывает при
и убывает при  . Соответствующие графики изображены на рис. A.6 и A.7.
. Соответствующие графики изображены на рис. A.6 и A.7.
Степенная функция обладает следующими свойствами:
1) произведение степенных функций с показателями  и
и  также степенная функция (с показателем
также степенная функция (с показателем  ):
):
 ;
;
2) композиция степенных функций с показателями  и
и  также степенная функция (с показателем
также степенная функция (с показателем  ):
):
 .
.
Показательная функция
Показательной функцией с основанием  (
( ,
,  )называется функция, определенная на множестве всех действительных чисел и ставящая в соответствие числу
)называется функция, определенная на множестве всех действительных чисел и ставящая в соответствие числу  число
число  .
.
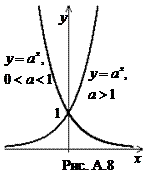 Область определения показательной функции
Область определения показательной функции  , область значений
, область значений  . Основное свойство показательной функции:
. Основное свойство показательной функции:  . При
. При  показательная функция возрастает,
показательная функция возрастает,  ,
, 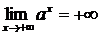 , при
, при  убывает,
убывает,  ,
,  . Для обоих случаев ее график изображен на рис. A.8.
. Для обоих случаев ее график изображен на рис. A.8.
В математическом анализе удобно работать с показательной функцией  с основанием
с основанием  . Она называется экспонентой и часто обозначается
. Она называется экспонентой и часто обозначается  . Показательные функции с другими основаниями сводятся к экспоненте:
. Показательные функции с другими основаниями сводятся к экспоненте: 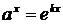 , где
, где  .
.
Логарифмическая функция
 Показательная функция
Показательная функция  возрастает (убывает) при
возрастает (убывает) при  (
( ) на всей области определения, поэтому существует обратная к ней функция, которую называют логарифмической функцией с основанием
) на всей области определения, поэтому существует обратная к ней функция, которую называют логарифмической функцией с основанием  (или просто логарифмом)и обозначают
(или просто логарифмом)и обозначают 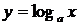 . Если
. Если  , то вместо
, то вместо  записывают
записывают  (натуральный логарифм), если
(натуральный логарифм), если  , то вместо
, то вместо 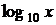 пишут
пишут  (десятичный логарифм).
(десятичный логарифм).
Основные свойства логарифмической функции:
1) область определения  ;
;
2) множество значений  ;
;
3) при  логарифмическая функция возрастает и
логарифмическая функция возрастает и  ,
,  ; при
; при  убывает и
убывает и  ,
,  ;
;
4)  ;
;
5)  ,
, 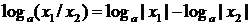 ;
;
6)  .
.
Графики логарифмической функцииизображены на рис. A.9.






