5.3.1. Вывести формулы (3) – (5) таблицы, используя первый замечательный предел, и формулы (6) – (8) таблицы, используя второй замечательный предел.
В задачах 5.3.1 – 5.3.5 сравнить функции.
5.3.2. 
и 
(
).
5.3.3. 
и 
(
).
5.3.4. 
и 
().
5.3.5. 
и 
(
).
5.3.6. Найти главную степенную часть функции 
и ее порядок (относительно 
) при 
.
5.3.7. Найти главную степенную часть функции 
и ее порядок (относительно ) при .
Вычислить пределы:
5.3.8.  .
| 5.3.9.  .
|
5.3.10.  .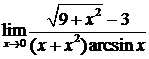
| 5.3.11.  .
|
5.3.12.  .
| 5.3.13.  .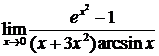
|
5.3.14.  .
| 5.3.15.  .
|
5.3.16.  .
| 5.3.17.  .
|
5.3.18.  .
| 5.3.19.  .
|
5.3.20.  .
| 5.3.21.  .
|
5.3.22.  .
| 5.3.23.  .
|
5.3.24.  .
| 5.3.25.  .
|
5.3.26.  .
| 5.3.27.  .
|
5.3.28.  .
| 5.3.29.  .
|
5.3.30.  .
| 5.3.31.  .
|
5.3.32.  .
| 5.3.33.  .
|
Непрерывные функции
Сведения из теории
Односторонние пределы
Говорят, что левый (соответственно, правый) предел функции 
в точке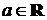 
равен 
(
), если для любого числа 
найдется такое число 
, что при 
и 
(соответственно 
) 
.
Обозначения: 
или 
(соответственно 
или 
).
Если функция определена в некоторой проколотой окрестности точки 
, то 
Û 
.
Понятие непрерывности
Функция f называется непрерывной в точке , если
,
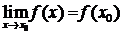то есть 
при всех 
и таких, что 
.
Обозначим 
– приращение аргумента в точке 
, 
– соответствующее ему приращение функции. В этих обозначениях определение непрерывности функции в точке примет вид
,
то есть при бесконечно малом изменении аргумента бесконечно мало меняются и значения непрерывной функции.
Если функция задана в некоторой окрестности точки , то определение непрерывности функции в точке можно записать в виде, использующем односторонние пределы:
.
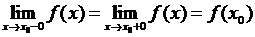Такой подход полезен при исследовании «сшитых» функций – функций, заданных при 
и 
разными формулами.
Функция называется непрерывной на множестве J, если она непрерывна в каждой точке 
.
Функция называется непрерывной, если она непрерывна в каждой точке своей области определения. Сумма, разность, произведение, частное, композиция непрерывных функций также непрерывные функции. Все элементарные функции непрерывны.
Точки разрыва и их классификация
Точкой разрыва функции называется точка 
, в которой функция определена, но не является непрерывной, то есть либо 
существует, но не совпадает со значением в точке: 
, либо не существует.
Если в точке разрыва функции существуют конечные пределы слева и справа: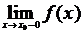 
и 
, но не совпадают между собой, то называется точкой разрыва 1 -го рода. Если же хотя бы один из этих пределов равен бесконечности или не существует, то называется точкой разрыва 2 -го рода.
Примеры решения задач
6.2.1. Доказать непрерывность синуса и косинуса.
◄ Пусть 
. Тогда для приращения функции в любой точке 
имеем
.
Поэтому , то есть синус – непрерывная функция.
Так как 
является композицией разности двух непрерывных функций 
и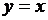 
с синусом, то косинус также непрерывная функция. ►
6.2.2. Найти односторонние пределы функции 
в точке 
.
◄ 
. 
.
Поэтому правый предел функции в точке
,
а левый предел функции в точке
.
В других обозначениях 
, 
. ►
6.2.3. Исследовать непрерывность функции 
◄ Если 
, то 
, так как элементарная функция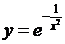 
определена и непрерывна в точке .
Если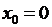 
, то
.
Таким образом, 
, то есть функция непрерывна во всех точках числовой прямой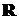 
. ►
6.2.4. Найти точки разрыва функции 
и определить их тип.
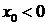
◄ При 
, при 
, то есть функция непрерывна в точках . Исследуем поведение функции в точке .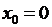
, 
. (6.1)
 |
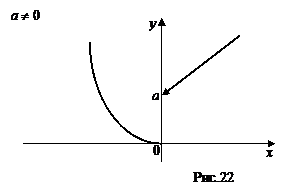При 
и потому – точка разрыва 1-го рода (рис. 22). При 
, следовательно, функция непрерывна в точке 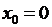(рис. 23). ►
