4.3.1. Пользуясь определением предела функции, убедиться, что
а) 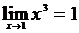 , б)
, б)  , в)
, в)  , г)
, г)  .
.
Найти пределы:
4.3.2.  . .
| 4.3.3.  . .
|
4.3.4. 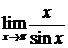 . .
| 4.3.5.  . .
|
4.3.6.  . .
| 4.3.7.  . .
|
4.3.8.  . .
| 4.3.9.  . .
|
4.3.10.  ; ;
| 4.3.11.  . .
|
4.3.12.  . .
| 4.3.13.  . .
|
4.3.14.  . .
| 4.3.15.  . .
|
4.3.16.  . .
| 4.3.17.  . .
|
4.3.18. 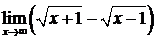 . .
| 4.3.19. 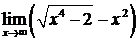 . .
|
4.3.20.  . .
| 4.3.21.  . .
|
4.3.22.  . .
| 4.3.23.  . .
|
4.3.24.  . .
| 4.3.25.  . .
|
4.3.26.  . .
| 4.3.27.  . .
|
4.3.28.  . .
| 4.3.29.  . .
|
4.3.30.  . .
| 4.3.31.  . .
|
4.3.32. 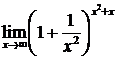 . .
| 4.3.33.  . .
|
4.3.34.  . .
| 4.3.35.  . .
|
4.3.36.  . .
| 4.3.37. 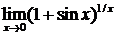 . .
|
АСИМПТОТИЧЕСКОЕ СРАВНЕНИЕ ФУНКЦИЙ
Сведения из теории
Основные понятия
Функция  называется бесконечно малой при
называется бесконечно малой при  (
( ), если
), если
 .
.
Функция  называется бесконечно большой при
называется бесконечно большой при  (
( ), если
), если
 .
.
При асимптотическом (предельном) исследовании относительного поведения функций  и
и  при
при  вычисляется
вычисляется  .
.
· Если  , то говорят, что функции
, то говорят, что функции  и
и  эквивалентны (или асимптотически равны) при
эквивалентны (или асимптотически равны) при  и пишут
и пишут  при
при  .
.
· Если  , где
, где  и
и 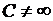 , то
, то  при
при  . В этом случае говорят, что функции
. В этом случае говорят, что функции  и
и  одного порядка при
одного порядка при  . Если при этом
. Если при этом  и
и  являются бесконечно малыми (бесконечно большими), то говорят что
являются бесконечно малыми (бесконечно большими), то говорят что  и
и  одного порядка малости (роста).
одного порядка малости (роста).
· Если  , то пишут
, то пишут  при
при  и говорят, что
и говорят, что  бесконечно мала по сравнению с
бесконечно мала по сравнению с  при
при  . Если при этом
. Если при этом  и
и  являются бесконечно малыми (бесконечно большими), то говорят, что
являются бесконечно малыми (бесконечно большими), то говорят, что  (
( ) более высокого порядка малости (роста) по сравнению с
) более высокого порядка малости (роста) по сравнению с  (
( ) при
) при  .
.
· Если  , то
, то 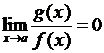 и
и  при
при  .
.
Если  при
при  , то говорят что
, то говорят что 
 -го порядка по сравнению с
-го порядка по сравнению с  при
при  . Ясно, что если
. Ясно, что если  и
и  являются бесконечно малыми (бесконечно большими), то при
являются бесконечно малыми (бесконечно большими), то при 
 и
и  одного порядка малости (роста), а при
одного порядка малости (роста), а при 
 более высокого порядка малости (роста) по сравнению с
более высокого порядка малости (роста) по сравнению с  .
.
Если  , то говорят что
, то говорят что  – главная степенная часть функции
– главная степенная часть функции  при
при  .
.
Свойства
1. Если  , то
, то  .
.
2. Если  и
и  , то
, то  .
.
3. Если  и
и 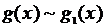 , то
, то
 и
и  .
.
4. Если  , то
, то  , где
, где  .
.
5. Если  , то
, то  , где
, где 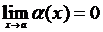 .
.
6.  Û
Û  Û
Û  .
.
7. Если  и
и 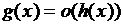 , то
, то  и
и
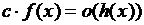 ,
,  при
при  .
.
В свойствах 1–7 подразумевается, что  .
.
8. Если  при
при  , то
, то  при
при  .
.
9. Если  при
при  , то
, то 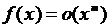 при
при  для
для  .
.
Основные эквивалентности
| № | Эквивалентность | Асимптотическая формула | При 
|
| 1 | 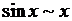
| 
| 
|
| 2 | 
| 
| 
|
| 3 | 
| 
| 
|
| 4 | 
| 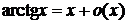
| 
|
| 5 | 
| 
| 
|
| 6 | 
| 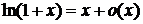
| 
|
| 7 | 
| 
| 
|
| 8 | 
| 
| 
|
| 9 | 
| 
|
Использование эквивалентностей
При нахождении пределов
Пусть  ,
, 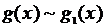 при
при  . Тогда
. Тогда

 ,
, 
 ,
,
если пределы в правых частях этих равенств существуют.
Примеры решения задач
5.2.1. Доказать, что  при
при  (формула (2) таблицы).
(формула (2) таблицы).
◄ Находим предел отношения функций:

 .
.
Предел равен 1, следовательно, функции эквивалентны при  :
:  . ►
. ►
5.2.2. Сравнить функции  и
и  при
при  .
.
◄ Заметим, что  и
и  бесконечно малые функции:
бесконечно малые функции:
 ,
,  .
.
Так как 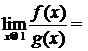
 , то
, то 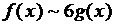 при
при  .
.
Это означает, что  и
и  бесконечно малые одного порядка (малости) при
бесконечно малые одного порядка (малости) при  . ►
. ►
5.2.3. Сравнить функции  и
и  при
при  .
.
◄ Эти функции являются бесконечно малыми при  :
: 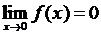 ,
,  . Вычислим
. Вычислим  , так как
, так как  и
и 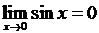 . Это означает, что
. Это означает, что  или
или 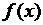 – бесконечно малая более высокого порядка по сравнению с
– бесконечно малая более высокого порядка по сравнению с  . ►
. ►
5.2.4. Сравнить функции 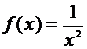 и
и  при
при  .
.
◄ Эти функции являются бесконечно большими при  :
:  ,
,  . Вычислим
. Вычислим 

 , так как
, так как  и
и  . Удобнее написать, что
. Удобнее написать, что 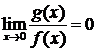 . Это означает, что
. Это означает, что  или
или  – бесконечно большая более высокого порядка (роста) по сравнению с
– бесконечно большая более высокого порядка (роста) по сравнению с  при
при  . ►
. ►
5.2.5. Найти главную степенную часть функции 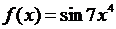 при
при  .
.
◄ Так как  при
при  , а
, а 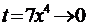 при
при  , то
, то  при
при  . То есть, главная степенная часть функции
. То есть, главная степенная часть функции  при
при  равна
равна  . ►
. ►
5.2.6. Найти главную степенную часть функции  и ее порядок (относительно
и ее порядок (относительно  ) при
) при  .
.
◄ Используем формулы (5) и (3) таблицы, свойства 2, 3 и тот факт, что  при
при  .
.
Получаем  и
и 


 или
или  . Таким образом, главная часть функции
. Таким образом, главная часть функции  при
при  равна
равна  , а ее порядок равен 2. ►
, а ее порядок равен 2. ►
5.2.7. Найти главную степенную часть функции

и ее порядок (относительно x) при  .
.
◄ Если в сумме функций заменить слагаемые на эквивалентные функции, то можно получить функцию не эквивалентную первоначальной[2]. Поэтому заменим каждое слагаемое на равную функцию, используя асимптотические формулы из последнего столбца таблицы.

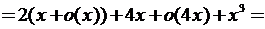
 .
.
По свойствам 7 и 9  ,
,  , и сумма трех слагаемых в скобке является также функцией
, и сумма трех слагаемых в скобке является также функцией  .
.
Получили, что  .
.
Таким образом, главная часть функции  при
при  равна
равна  , а порядок относительно бесконечно малой x равен 1. ►
, а порядок относительно бесконечно малой x равен 1. ►
5.2.8. Сравнить функции  и
и  при
при  .
.
Решение 1.
◄ Так как 


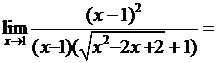
 ,
,
то 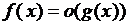 при
при  , то есть
, то есть  – бесконечно малая более высокого порядка по сравнению с
– бесконечно малая более высокого порядка по сравнению с  . ►
. ►
Решение 2.
◄ 
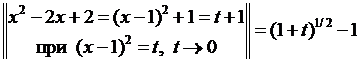 .
.
По формуле (8) таблицы  , и потому
, и потому 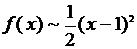 при
при  , то есть
, то есть  имеет при
имеет при  второй порядок (относительно «простейшей» бесконечно малой
второй порядок (относительно «простейшей» бесконечно малой  ). По сравнению с решением 1 получен более точный результат. ►
). По сравнению с решением 1 получен более точный результат. ►
5.2.9. Вычислить  .
.
◄ При вычислении предела отношения числитель и знаменатель (согласно 5.1.3) можно заменить эквивалентными функциями. Переходя к натуральным логарифмам и используя формулы (2) и (6) таблицы эквивалентностей и свойства 2 - 3, получаем
 ,
,
 .
.
Поэтому  =
=  . ►
. ►
5.2.10. Вычислить  .
.
◄ В примере 4.2.5 найден этот предел двумя способами. Проще всего вычислить его, используя формулу (9) таблицы эквивалентностей:
 =
=  . ►
. ►
5.2.11. Вычислить  .
.
◄ 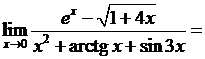


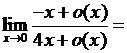
 . ►
. ►
5.2.12. Вычислить  .
.
◄ Воспользуемся «основным логарифмическим тождеством» 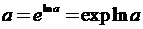
 :
:
 =
=  по непрерывности
по непрерывности 
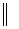 =
=

 =
=  . ►
. ►
5.2.13. Вычислить  .
.
◄  =
= 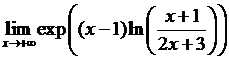 .
.
Так как  =
=  , а
, а  , то
, то  .
.
Поскольку  , то
, то  . ►
. ►




