3.3.1. Доказать, пользуясь определением, что  . Составить таблицу.
. Составить таблицу.

| 0,1 | 0,01 | 0,001 |

|
3.3.2. Доказать, пользуясь определением, что  .
.
Вычислить пределы последовательностей:
3.3.3.  . .
| 3.3.4.  . .
|
3.3.5.  . .
| 3.3.6.  . .
|
3.3.7.  . .
| 3.3.8.  . .
|
3.3.9.  . .
| 3.3.10.  . .
|
3.3.11. Последовательность  задана рекуррентно:
задана рекуррентно:  и
и 
 . Доказать, что она сходится и найти ее предел.
. Доказать, что она сходится и найти ее предел.
3.3.12. Доказать, что последовательность  =
=  , где
, где  – целая часть числа
– целая часть числа  , сходится и найти ее предел.
, сходится и найти ее предел.
3.3.13. Доказать, что последовательность  , где
, где  , сходится, а последовательность
, сходится, а последовательность  , где
, где  , расходится.
, расходится.
ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ
Сведения из теории
Определение предела функции
Пусть  и
и  принадлежат расширенной числовой прямой
принадлежат расширенной числовой прямой  , то есть являются либо действительными числами, либо одним из символов
, то есть являются либо действительными числами, либо одним из символов  ,
,  . Предположим, что в любой проколотой окрестности точки
. Предположим, что в любой проколотой окрестности точки  есть хотя бы одна точка из области определения
есть хотя бы одна точка из области определения 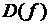 функции
функции  .
.
Говорят, что предел функции  в точке
в точке  (при
(при  , стремящемся к
, стремящемся к  ) равен
) равен  , если для любой окрестности
, если для любой окрестности 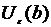 точки
точки  найдется такая проколотая окрестность
найдется такая проколотая окрестность 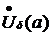 точки
точки  , что как только
, что как только 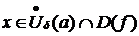 так
так  .
.
Обозначения:  или
или  при
при  .
.
В краткой записи



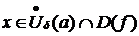

 .
.
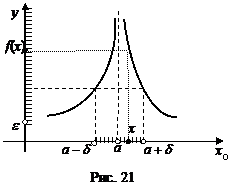 «Переведем» это определение на язык неравенств для двух случаев.
«Переведем» это определение на язык неравенств для двух случаев.

 1) Пусть
1) Пусть  .
.


 (
(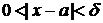

 )(рис. 20).
)(рис. 20).
2) Пусть  , а
, а  .
.



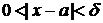

 (рис. 21).
(рис. 21).
Конечно, в случае 1)  означает, что
означает, что  можно взять сколь угодно малым, а в случае 2) сколь угодно большим.
можно взять сколь угодно малым, а в случае 2) сколь угодно большим.
Остальные 14 возможных случаев рекомендуется разобрать и проиллюстрировать самостоятельно.
Вычисление пределов непрерывных функций
В точках из их областей определения
Если предел функции в точке равен значению функции в этой точке:
 , (4.1)
, (4.1)
то функция называется непрерывной в этой точке. Можно показать, что любая элементарная функция непрерывна в каждой точке ее области определения, и потому ее предел в такой точке можно найти по формуле (4.1).
Арифметические операции над пределами
Пусть  ,
, 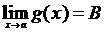 . Тогда
. Тогда
1)  (
( ).
).
2) 
3) 
4) 
В этих равенствах условные записи  ,
,  ,
,  и
и  означают, что при вычислении соответствующего предела имеет место неопределенность: при указанных значениях A и B предел может быть любым или не существовать в зависимости от конкретного вида функций
означают, что при вычислении соответствующего предела имеет место неопределенность: при указанных значениях A и B предел может быть любым или не существовать в зависимости от конкретного вида функций  и
и  . Методы вычисления пределов в случаях неопределенности (раскрытия неопределенности) рассматриваются ниже в разделах 4.2, 5.1.4, 5.2 и в дифференциальном исчислении (например, в методических указаниях [1]).
. Методы вычисления пределов в случаях неопределенности (раскрытия неопределенности) рассматриваются ниже в разделах 4.2, 5.1.4, 5.2 и в дифференциальном исчислении (например, в методических указаниях [1]).
Предел сложной функции. Замена переменных в пределах
1. Пусть  ,
,  при
при  . Тогда, если
. Тогда, если 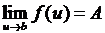 , то
, то

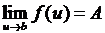 .
.
2. Пусть  и функция f непрерывна в точке b. Тогда
и функция f непрерывна в точке b. Тогда
 .
.
Два замечательных предела
Первый замечательный предел
 .
.
Второй замечательный предел  равен некоторому иррациональному действительному числу, которое называется числом Эйлера и обозначается буквой
равен некоторому иррациональному действительному числу, которое называется числом Эйлера и обозначается буквой  (
(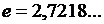 ). Итак,
). Итак,
 .
.
Сделав замену  , получим другую форму второго замечательного предела
, получим другую форму второго замечательного предела
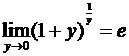 .
.
С числом Эйлера  связаны функции: экспонента
связаны функции: экспонента  и натуральный логарифм
и натуральный логарифм  .
.
Примеры решения задач
4.2.1. Пользуясь определением предела функции в точке, убедиться, что  .
.
◄ Надо доказать, что для любого  найдется
найдется  , такое что
, такое что
 .
.
По свойству абсолютной величины  .
.
Выберем 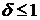 , тогда
, тогда 


 .
.
Возьмем 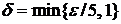 , тогда
, тогда  . ►
. ►
4.2.2. Найти  .
.
◄ Функция  является элементарной и
является элементарной и  точка ее области определения, поэтому
точка ее области определения, поэтому  непрерывна в точке
непрерывна в точке  , то есть
, то есть  или
или  . ►
. ►
4.2.3. Найти  .
.
◄ Функция  не определена в точке
не определена в точке 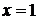 , поэтому для вычисления предела нельзя воспользоваться непрерывностью функции. Так как
, поэтому для вычисления предела нельзя воспользоваться непрерывностью функции. Так как  ,
,  , то по правилу вычисления предела частного
, то по правилу вычисления предела частного  . ►
. ►
4.2.4. Найти  .
.
Решение 1.
◄ Так как  ,
,  , то имеем неопределенность
, то имеем неопределенность  . Сделаем тождественное преобразование дроби, позволяющее избавиться от неопределенности. Так как
. Сделаем тождественное преобразование дроби, позволяющее избавиться от неопределенности. Так как 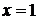 и
и  – корни числителя, а
– корни числителя, а 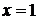 и
и  корни знаменателя, то
корни знаменателя, то 
 . ►
. ►
Решение 2.
◄ Сделаем замену:  , тогда
, тогда  . Если
. Если  , то
, то  .
.
 . ►
. ►
4.2.5. Найти  .
.
Решение 1.
◄Сделаем замену  . Если
. Если  , то
, то  .
.
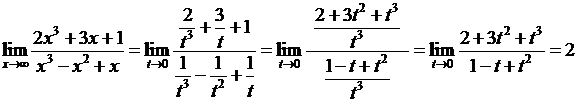 . ►
. ►
Решение 2.
◄ Сделаем тождественное преобразование дроби, разделив числитель и знаменатель почленно на  .
.
 . ►
. ►
4.2.6. Найти  .
.
Решение 1.
◄ 

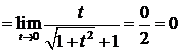 . ►
. ►
Решение 2.
◄  . ►
. ►
4.2.7. Найти  .
.
◄ Имеем неопределенность  . Чтобы избавиться от иррациональности, сделаем замену
. Чтобы избавиться от иррациональности, сделаем замену  . Если
. Если  , то
, то  .
.
 . ►
. ►
4.2.8. Найти  .
.
◄ Используем первый замечательный предел.
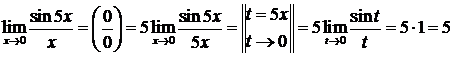 . ►
. ►
4.2.9. Найти  .
.
◄ Имеем неопределенность  . Заменим
. Заменим  и получим неопределенность
и получим неопределенность  :
:
 . ►
. ►
4.2.10. Найти  .
.
◄ Так как в первом замечательном пределе аргумент стремится к нулю, то сделаем замену переменной:  . Тогда
. Тогда  при
при  .
.

 ►
►
4.2.11. Найти  .
.
◄ Используем второй замечательный предел.
 . ►
. ►
4.2.12. Найти 
◄ 
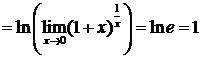 . ►
. ►






