Найти области определения и области значений функций.
2.3.1.  .
| 2.3.2.  .
|
2.3.3.  .
| 2.3.4.  .
|
2.3.5. Найти 
, если 
2.3.6. Найти 
, если 
2.3.7. Является ли функция 
элементарной?
2.3.8. Найти 
. Записать произведение функций 
в виде степенной функции, если
а) 
. б) 
.
Найти композиции 
, 
и их области определения.
2.3.9.  .
| 2.3.10.  .
|
Убедиться, что заданная функция 
имеет обратную 
и найти ее аналитическое выражение.
2.3.11.  .
| 2.3.12.  .
|
Построить графики следующих функций:
2.3.13.  .
| 2.3.14.  .
|
2.3.15.  .
| 2.3.16.  .
|
2.3.17.  .
| 2.3.18.  .
|
2.3.19.  .
| 2.3.20.  .
|
2.3.21.  .
| 2.3.22.  .
|
2.3.23.  .
| 2.3.24.  .
|
2.3.25.  .
| 2.3.26.  .
|
2.3.27.  .
| 2.3.28.  .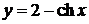
|
2.3.29.  .
| 2.3.30.  .
|
2.3.31.  .
| 2.3.32.  .
|
2.3.33.  .
| 2.3.34.  .
|
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
3.1. 
Сведения из теории
Расширенная числовая прямая. Окрестности точек
 |
Добавим к числовой прямой
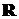еще два элемента 
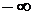и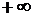 
(«бесконечно удаленные точки»). Получим расширенную числовую прямую 
. Ее модель в виде полуокружности изображена на рис. 17. Другой вариант расширенной числовой прямой получим, если отождествить 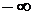и ( = =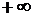 
): 
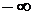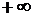. Ее модель в виде окружности изображена на рис. 18.
Для любого числа 
определим ε-окрестность точки 
:
если 
, то
(рис. 19),
если 
, то
(рис. 17),
если 
, то
(рис. 17),
если 
, то
(рис. 18).
Проколотая ε-окрестность точки : 
.
Последовательность и ее предел
Последовательностью называется функция 
, ставящая в соответствие каждому натуральному числу n действительное число 
(называемое n -м членом последовательности).
Будем обозначать последовательность – 
.
Говорят, что предел последовательности равен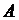 
(
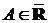), если для любой окрестности 
точки 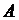найдется номер 
, начиная с которого все члены последовательности принадлежат , то есть
.
Обозначения: 
, 
или 
.
Таким образом,
.
.
.
.
Единственность предела. Если у последовательности существует предел, то он единственный.
Свойства пределов последовательностей
1. 
, где С – постоянная.
Если существуют конечные пределы и 
, то справедливы следующие свойства:
2. 
.
3. 
.
4. 
.
5. 
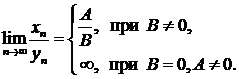
6. Если 
, а 
, то 
.
Признаки сходящихся последовательностей
Последовательности, имеющие конечный предел, называются сходящимися, имеющие бесконечный предел или вообще его не имеющие, – расходящимися.
Теорема 1 (о сходимости монотонной ограниченной последовательности)
а) Если последовательность – неубывающая, то есть 
и, если она ограничена сверху, то есть 
, то она сходится; при этом 
.
б)Если последовательность – невозрастающая, то есть 
и, если она ограничена снизу, то есть 
: 
, то она сходится; при этом 
.
Теорема 2 (Критерий Коши) (необходимое и достаточное условие сходимости последовательности). Последовательность сходится тогда и только тогда, когда для каждого e > 0 существует такое натуральное число 
, что неравенство 
выполняется при всех 
.
Теорема 3 (о пределе промежуточной последовательности)
Если 
, а 
, то и 
.
Примеры решения задач
3.2.1. Доказать, что 
, пользуясь определением предела последовательности.
◄ Пусть 
. Надо доказать, что для любого числа найдется такое натуральное число 
, что 
. Так как
,
то
.
Возьмем 
– следующее за 
целое число[1].
Тогда при 
, то есть .
При 
.
При 
.
При 
. ►
3.2.2. Доказать, что 
, пользуясь определением предела последовательности.
◄ Обозначим 
. Надо доказать, что 
можно подобрать натуральное так, чтобы 
.
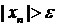Так как 
то
.
Взяв 
, получим, что 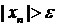, то есть 
. ►
3.2.3. Найти предел 
.
◄ Разделим числитель и знаменатель дроби на 
– наибольшую из степеней n в числителе и знаменателе:
. ►
3.2.4. Последовательность задана рекуррентно: 
и 
. Доказать, что она сходится и найти ее предел.
◄ Выпишем несколько членов последовательности: , 
, 
, 
.
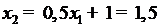По ним можно предположить, что последовательность не убывает и ограничена сверху числом 2. Докажем это. Пусть 
. Тогда 
и действительно 
. По теореме 1 последовательность сходится, то есть существует конечный 
. Переходя в равенстве 
к пределу, используя свойства 1) – 3), получаем 
, откуда 
. ►
3.2.5. Доказать, что последовательность = 
, где 
– целая часть числа 
, сходится и найти ее предел.
◄ Ясно, что
.
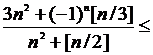
Так как 
, 
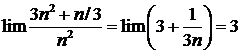, то по теореме о пределе промежуточной последовательности сходится и ее предел равен 3.
3.2.6. Доказать, что последовательность , где 
, сходится. Здесь 
– произведение всех натуральных чисел от 1 до 
включительно.
◄ Применим критерий Коши. Зададим . При 
(сумма геометрической прогрессии)=
= 
.
Выбрав теперь 
, будем иметь при
.
Согласно критерию Коши последовательность сходится. Можно доказать, что 
, где 
– число Эйлера (см. 4.1.5). ►
