1.3.1. Задать следующие множества перечислением элементов.
а)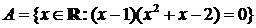 
; б) 
.
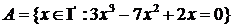1.3.2. Пусть 
, 
.
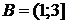Найти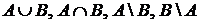 
, 
, 
, 
, 
.
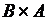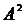1.3.3. Найти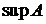 
, 
, 
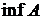
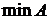(если они существуют) для следующих множеств.
a) 
; б)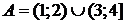 
.
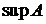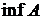
1.3.4. Найти , , 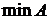(если они существуют) для следующих множеств.
a) 
; б) 
.
Выяснить смысл приведенных высказываний и установить, истинны они или ложны.
1.3.5.  .
| 1.3.6.  .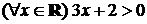
|
1.3.7.  .
| 1.3.8.  .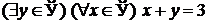
|
1.3.9.  .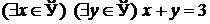
| 1.3.10.  .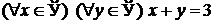
|
1.3.11.  .
| 1.3.12.  .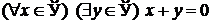
|
1.3.13.  .
| 1.3.14.  .
|
ФУНКЦИИ
Сведения из теории
Основные понятия
Пусть 
– некоторое множество действительных чисел. Говорят, что на множестве задана (числовая) функция 
если каждому числу 
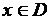(аргументу функции) поставлено в соответствие единственное число, обозначаемое 
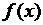и называемое значением функции в точке x. Множество 
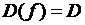называется областью определения функции, а множество 
- областью значений функции.
Функция обозначается также 
или 
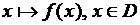, или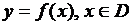 
, или просто 
.
Графиком функции f (рис. 7) называется множество
.
Наиболее распространенным способом задания функций является аналитический. Он состоит в том, что с помощью формулы задается алгоритм вычисления значения функции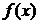 
по значению ее аргумента x. В этом случае область определения обычно не указывают, понимая под ней множество всех тех значений x, при которых данная формула имеет смысл.
Арифметические операции над функциями
Суммой (разностью) функций 
и 
называется функция 
(
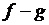), определенная на множестве 
, значение которой в точке 
вычисляется по формуле
.
Произведением функций и называется функция 
, определенная на множестве , значение которой в точке вычисляется по формуле
.
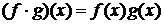Частным функций и называется функция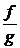 
, определенная на множестве 
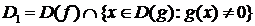, значение которой в точке 
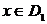вычисляется по формуле 
.
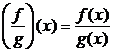Композиция функций
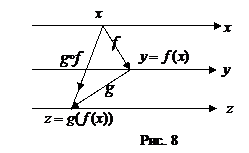
Композицией функций и (или сложной функцией, полученной композицией функций и ) называется функция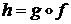 
(рис. 8), задаваемая формулой 
на множестве 
.
Обратная функция
Пусть функция 
такова, что 
,
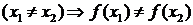например, – возрастает:
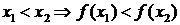
или – убывает:
.
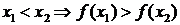Тогда для любого 
найдется единственное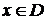 
, такое что 
. Тем самым определена функция 
, 
, называемая функцией обратной к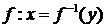 
(рис. 9).
Ясно, что
, 
,
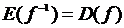и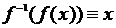 
.
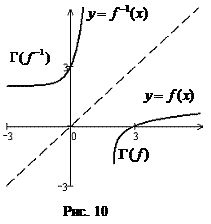График 
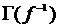обратной функции получается из 
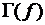преобразованием плоскости 
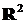, переводящим любую точку 
в точку 
, симметричную ей относительно прямой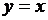 
(рис. 10).
Элементарные функции
Следующие функции называются основными элементарными функциями:
1) постоянная функция 
;
2) степенная функция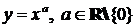 
;
3)
|
;
4) логарифмическая функция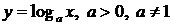 
;
5) тригонометрические функции 
;
6) обратные тригонометрические функции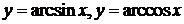 
, 
.
Их определения, свойства и графики приведены в приложении A.
Элементарной функцией называется функция, которая может быть получена из основных элементарных функций с помощью конечного числа арифметических операций и операции композиции.
Примерами элементарных функций являются гиперболические функции: синус гиперболический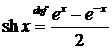 
и косинус гиперболический 
. Их свойства и графики также приведены в приложении A.
Примером неэлементарной функции является функция сигнум (функция «знак»), заданная формулой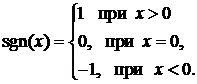 
Преобразование графиков
Если Г – график функции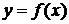 
, то
1) график функции 
симметричен Г относительно оси Ox;
2) график функции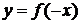 
симметричен Г относительно оси Oy;
3) график функции 
, получается сдвигом Г вдоль оси Ox вправо на a при 
влево на 
, при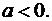 
4) график функции 
, получается сдвигом Г вдоль оси Oy вверх на b, при 
, вниз на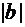 
, при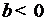 
;
5) график функции 
, получается сжатием Г в a раз (при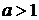 
) или растяжением в 
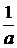раз (при 
) вдоль оси Ox;
6) график функции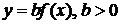 
, получается растяжением Г в b раз (при 
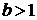) или сжатием в 
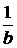раз (при 
) вдоль оси Oy.
Примеры решения задач
2.2.1. Найти область определения и область значений функции, заданной формулой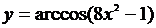 
.
◄ Функция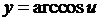 
определена при значениях аргумента 
. Поэтому рассматриваемая функция определена при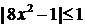 
. Решаем это неравенство: 
.
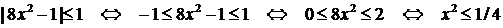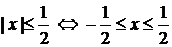. Итак, 
. ►
2.2.2. Убедиться, что функция синус гиперболический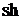 
имеет обратную 
(обозначаемую также 
). Выразить ее через основные элементарные функции.
◄ Областью значений функции 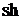является множество всех действительных чисел. Докажем, что для любого 
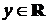уравнение 
, то есть уравнение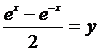 
, имеет относительно 
единственное решение и найти его. Перепишем уравнение в виде 
. Оно равносильно совокупности уравнений
.
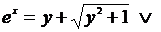
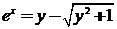Второе из этих уравнений имеет отрицательную правую часть и потому решений не имеет, а первое имеет единственное решение 
. Итак,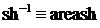 
существует и задается формулой
. ►
2.2.3. Найти композици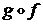и 
и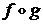 
функций f и g, если 
, 
.
◄ 
;
. ►
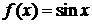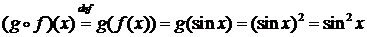2.2.4. 
Построить график функции 
.
◄ Выделим полный квадрат:
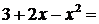
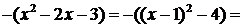
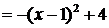. Поэтому график функции получается из параболы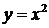 
путем последовательных преобразований: 1) сдвигом вдоль оси Ох на единицу вправо; 2) симметрией относительно оси О х; 3) сдвигом вдоль О y вверх на 4 единицы (рис. 11). ►
2.2.5. Построить график функции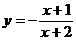 
.
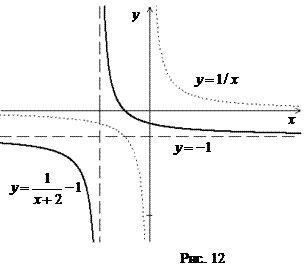◄ Преобразуем правую часть следующим образом:
.
Поэтому функцию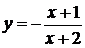 
можно записать в виде 
. Ее график получается из графика функции 
(гиперболы) сдвигом вдоль оси Ox на 2 влево и вдоль оси Oy на 1 вниз (рис. 12). ►
2.2.6. 
Построить график функции 
.
◄ По определению модуля действительного числа имеем
График логарифмической функции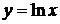 
, сначала сдвигаем вдоль оси Ox на 1 влево. Затем часть графика, расположенную над осью Ox оставляем без изменения, а часть графика, расположенную под осью Ox отражаем симметрично относительно оси Ox (рис. 13). ►
2.2.7. Построить график функции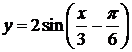 
.
 |
◄ Так как
, то график функции получается из синусоиды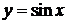 
путем следующей цепочки преобразований: 1) сдвигом на 
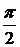вправо получается график функции 
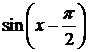(рис. 14);
2) растяжением вдоль оси Ox в 3 раза предыдущего графика получается график функции 
; 3) график функции 
получается растяжением вдоль оси Oy в 2 раза (рис. 15). ►
