ВВЕДЕНИЕ В АНАЛИЗ
Методические указания
Ярославль 2009
УДК 517(07)
МУ 26-09. Введение в анализ: методические указания / сост.: Ю.К. Оленикова, В.Ш. Ройтенберг, Л.А. Сидорова. – 3-е изд., испр. и доп. – Ярославль: Изд-во ЯГТУ, 2009. – 44 с.
Содержат краткие теоретические сведения по разделу «Введение в анализ», подробно разобранные типовые задачи, даны задачи для самостоятельного решения. Могут быть использованы студентами на практических занятиях и при выполнении домашних заданий.
Предназначены для студентов 1-го курса всех специальностей очного отделения.
Библиогр. 7. Прил. 1.
Рецензенты: кафедра высшей математики Ярославского государственного технического университета; Ю.И. Большаков, канд. физ.-мат. наук, доцент кафедры общей математики Ярославского государственного университета им. П.Г. Демидова.
____________________________________________________________________
План 2009
Редактор М.А. Канакотина
Подписано в печать 8.04.09. Формат 60х84 1/16. Бумага белая.
Печать ризограф. Усл. печ. л. 2,56. Уч.-изд. л. 2,51.
Тираж 1000. Заказ 388.
Ярославский государственный технический университет
150023, Ярославль, Московский пр., 88
Типография Ярославского государственного технического университета
150000, Ярославль, ул. Советская, 14а
____________________________________________________________________
Ó Ярославский государственный технический университет, 2009
МНОЖЕСТВА
Сведения из теории
Логическая символика
Под высказыванием понимают предложение, о котором имеет смысл говорить, что оно истинно или ложно.
Отрицанием высказывания a называется высказывание, обозначаемое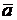 
(читается «не а»), которое истинно тогда и только тогда, когда а ложно.
Конъюнкцией высказываний а и 
называется высказывание, обозначаемое 
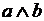(читается «а и b», «а конъюнкция b»), которое истинно тогда и только тогда, когда истинны оба высказывания а и b.
Дизъюнкцией высказываний а и b называется высказывание обозначаемое 
(читается «а или b», «а дизъюнкция b»), которое истинно тогда и только тогда, когда истинно хотя бы одно из высказываний а или b.
Импликацией высказываний а и b называется высказывание обозначаемое 
(читается «если а, то b», «из а следует b»), которое ложно тогда и только тогда, когда высказывание а истинно, а b ложно.
Высказывания а и b равносильны (эквивалентны), если 
. В этом случае пишут 
.
Квантор всеобщности 
ставит в соответствие каждому высказыванию 
, зависящему от переменного 
, принадлежащего некоторому множеству 
, высказывание, обозначаемое 
(читается «для всех 
справедливо »), истинное тогда и только тогда, когда истинно при всех .
Квантор существования 
ставит в соответствие каждому высказыванию , , высказывание, обозначаемое 
(читается «существует такое, что справедливо »), истинное тогда и только тогда, когда истинно хотя бы при одном .
Множества
Множество – это совокупность (коллекция, собрание,...) каких-то объектов, называемых элементами множества.
Удобно ввести пустое множество 
– множество, не содержащее ни одного элемента.
Если объект x – элемент множества A (принадлежит множеству A), то пишут 
, в противном случае пишут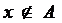 
. Если любой элемент множества A является и элементом множества B, то говорят, что множество A – подмножество (часть) множества B и пишут 
.
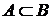Множества A и B называются равными (
), если совпадают их элементы, то есть 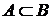и 
.
Существует два наиболее употребительных способа задания множеств.
· Конечное множество А задается перечислением всех его элементов 
. Это записывается так: 
, где все 
(
) различны.
· Подмножество A известного множества U можно задать указанием свойства (S), которому подчиняются все элементы данного множества. Это записывается так: 
обладает свойством 
.
Операции над множествами
Договоримся, что все рассматриваемые множества являются подмножествами некоторого множества U.
Объединением множеств A и B (рис.1) называется множество, обозначаемое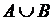 
и состоящее из элементов, принадлежащих хотя бы одному из множеств А или В:
= 
.
Пересечением множеств A и B (рис. 2) называется множество, обозначаемое 
и состоящее из элементов, принадлежащих обоим множествам А и В:
= 
.
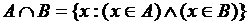Разностью двух множеств A и B (рис.3) называется множество
.
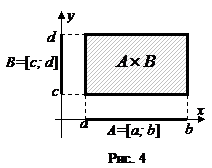Декартовым произведением множеств A и B (рис.4) называется множество
.
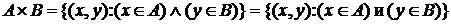Вместо 
обычно пишут 
.
Числовые множества
Из школьной программы известны следующие числовые множества:
· 
– множество натуральных чисел;
· 
– множество целых чисел;
· 
– множество рациональных чисел;
· 
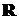– множество действительных (вещественных) чисел.
При этом 
.
Действительные числа изображаются точками числовой прямой.
Промежутками называются следующие подмножества множества действительных чисел:
открытый промежуток, или интервал, 
;
замкнутый промежуток, или отрезок, 
;
а также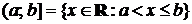 
, 
, 
, 
, 
, 
. Здесь 
и – действительные числа,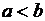 
.
Верхние и нижние грани числовых множеств
Множество A (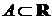
) называется ограниченным сверху, если (
) (
): 
, в противном случае множество А называется неограниченным сверху. При этом число М называется верхней гранью множества А. Наименьшая из всех верхних граней (она всегда существует) называется точной верхней гранью множества А и обозначается 
(супремум А). Если множество A неограниченно сверху, то полагают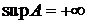 
.
Множество A (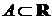) называется ограниченным снизу, если (
) (
): 
, в противном случае множество А называется неограниченным снизу. При этом число 
называется нижней гранью множества А. Наибольшая из всех нижних граней (она всегда существует) называется точной нижней гранью множества А и обозначается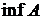 
(инфимум А). Если множество А неограниченно снизу, то полагают 
.
Множество А называется ограниченным, если оно ограничено сверху и снизу.
Будем обозначать через 
и 
соответственно наибольший и наименьший элемент множества А, когда они существуют, и в этом случае 
, 
.
Примеры решения задач
1.2.1. Задать множество 
перечислением элементов.
◄ Множество А состоит из натуральных решений неравенства 
. Решая его, получим 
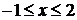, то есть 
. ►
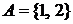1.2.2. Найти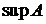 
, , 
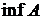
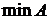(если они существуют), для множества 
.
◄ 
, 
, 
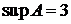не существует. ►
1.2.3. Пусть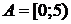 
, 
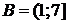. Найт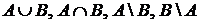и 
, 
и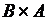 
.
◄ 
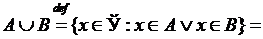
(рис. 5).
.
.
.
.
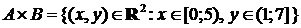(рис. 6). ►
1.2.4. Истинны ли следующие высказывания
;
?
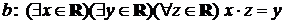◄ Высказывание состоит в том, что для любого действительного числа и любого действительного числа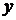 
существует такое действительное число 
, что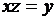 
. Ясно, что это утверждение ложно, так как при 
, 
такое не существует. Высказывание состоит в том, что существуют такие действительные числа и 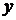, что для любого действительного числа , что 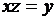. Это высказывание истинно. Можно взять , 
. Тогда для любого имеем 
. ►
