Упражнение №1. Определение коэффициента вязкости методом Стокса

Метод основан на измерении скорости движения шариков диаметром 1–2 мм при прохождении фиксированного расстояния . Когда шарик попадает в жидкость, на него действуют три силы: сила тяжести, направленная вниз; выталкивающая сила (сила Архимеда), направленная вверх; сила внутреннего трения, также направленная вверх. Сила внутреннего трения (вязкость) как и все силы трения, прямо пропорциональна скорости движения тела. Таким образом, по мере ускорения шарика под действием силы тяжести и увеличения его скорости, сила трения будет возрастать. Этот процесс будет продолжаться до тех пор, пока сила внутреннего трения плюс сила Архимеда не уравновесят силу тяжести. После этого шарик будет двигаться равномерно. Опыт показывает, что условия равновесия наблюдаются уже после прохождения шариком первых 8–10 см. Следовательно, первая метка ставится на расстоянии 10 см от края жидкости.

Запишем закон движения шарика после прохождения первой метки (первый закон Ньютона):

Итак, на шарик действуют три силы:

П о движению – сила тяжести:

Р = mg = V g = π r³ g, (1)

г где - плотность вещества шарика;

V - объем; V= π r³ (r- радиус шарика);

g - ускорение силы тяжести.

Против движения – сила Архимеда:

F_А = _ж Vg = π r³ _жg, (2)

где _ж – плотность исследуемой жидкости.

Сила трения (формула Стокса)

F_тр = 6 πrη , (3)

где – скорость движения шарика, и определяется по формуле: = (t – время движения шарика).

Используя первый закон Ньютона, запишем соотношение между силами:

Р = F_А + F_тр или Р − F_А = F_тр. (4)

Подставляем значение сил Р; F_А; F_тр из формул (1), (2), и (3) в уравнение (4):

πr³ g – π r³ _жg, = 6 πr η ;

π r³ g ( - _ж) = 6 πr η .

Отсюда определяем коэффициент вязкости:

η = = – рабочая формула.

Порядок выполнения работы

1. С помощью штангенциркуля измеряем диаметр шарика и определяем его радиус.

2. С помощью таблиц справочника определяем значение плотностей шарика и исследуемой жидкости.

3. С помощью линейки определяем расстояние между метками

4. Опускаем шарик как можно ближе к центру сосуда. При прохождении шариком верхней метки (расположить ее на уровне глаз) включаем секундомер, при пересечении шариком нижней метки секундомер выключаем. Определяем время t.

5. Аналогичные опыты проводим с четырьмя шариками.

6. Данные заносим в таблицу:

№	(см)	t (с)			_ж	g	η(Пз)	Δη(Пз)	· 100	Дов. инт. (mt)
1	2	3	4	5	6	7	8	9	10




						Сред- ние

Упражнение №2. Определение коэффициента вязкости с помощью

Вискозиметра.

В медицинской практике величина коэффициента вязкости определяется с помощью вискозиметра Гесса (метод называется вискозиметрией).

Измерение вязкости с помощью капиллярного вискозиметра основано на определении времени истечения жидкости через капилляр из рабочего объема прибора:

– рабочая формула, где

к – постоянная прибора (входит в паспорт прибора);

t – время истечения жидкости;

– плотность жидкости (необходимо найти по таблицам).

Порядок выполнения работы

1. Заполнить вискозиметр исследуемой жидкостью выше верхней риски, ограничивающей рабочий объем.

2. В момент прохождения жидкости через верхнюю риску включить секундомер, а в момент прохождения жидкости через нижнюю метку секундомер выключить определить время t.

3. Опыт повторить пять раз.

4. Полученные данные занести в таблицу.

№ п/п	к	t	η	Δη	·100	Доверительный интервал (mt)





ср.
ср.

Контрольные вопросы

1. Ламинарное и турбулентное течение жидкости. Число Рейнольдса.

2. Основной закон вязкого течения. Уравнение Ньютона.

3. Коэффициенты динамической и кинематической вязкости. Текучесть жидкости.

4. Формула распределения скоростей течения жидкости в цилиндрическом сосуде.

5. Объемная скорость течения жидкости. Уравнение Пуазейля.

6. Уравнение неразрывности струи.

7. Уравнение Бернулли.

8. Определение коэффициента вязкости методом Стокса.

Тестовые задания

1. Число Рейнолдса можно посчитать по формуле:

а) ; б) ;

в) ; г) .

В этих формулах R – радиус трубы, - плотность жидкости, – средняя по сечению трубы скорость течения, - коэффициент динамической вязкости.

2. Уравнение Ньютона для силы трения (F_тр) между слоями ламинарно текущей жидкости можно записать в виде:

а) F_тр = S; б) F_тр = η S;

в) F_тр= η ; г) F_тр= η S.

где - разность скоростей между слоями ламинарно текущей жидкости, 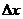- расстояние между этими слоями, η – коэффициент динамической вязкости, S - площадь соприкосновения слоев.

3. В уравнении Бернулли:

а) P – весовое давление, – статическое давление, – динамическое давление;

б) P – статическое давление, – весовое давление, – динамическое давление;

в) P – статическое давление, – динамическое давление, – весовое давление;

г) P – динамическое давление, – весовое давление, – статическое давление.

4. Уравнение Бернулли выводится на основании:

а) первого закона Ньютона; б) второго закона Ньютона;

в) уравнения Ньютона для течения вязкой жидкости;

г) закона сохранения энергии.

5. Укажите единицу измерения коэффициента кинематической вязкости в системе СИ:

а) Па·с; б) Стокс; в) Пуаз; г) м²/с.

6. Укажите формулу коэффициента кинематической вязкости:

а) ; б) ; в) ; г) .

7. Укажите формулу текучести жидкости:

а) ; б) ; в) ; г) .

8. Распределение линейной скорости течения жидкости по трубе (V, м/с) определяется соотношением:

а) ; б) ;

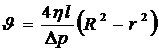в) ; г) .

9. Средняя линейная скорость течения крови по сосудам максимальна:

а) в капиллярах; б) в венах; в) в артериолах; г) в аорте.

10. Укажите уравнение Пуазейля для объемной скорости течения жидкости (Q):

а) ; б) ; в) ; г) .

11. Укажите единицу измерения объемной скорости кровотока:

а) м²/с; б) м/с; в) м³/с; г)м/с².

12. Выберите правильное утверждение:

а) объемная скорость кровотока максимальна на уровне аорты;

б) объемная скорость кровотока минимальна на уровне капилляров;

в) объемная скорость кровотока постоянна на всех уровнях ветвления.

13. Укажите формулу определения гидравлического сопротивления R:

а) б)

в) г)

14. Укажите уравнение неразрывности струи:

а) Q = / S = const; б) Q = · S = const; в) Q = S/ = const; г) Q = const/S .

15. Укажите формулу Стокса для силы трения (Fтр) в случае шарика, движущегося в вязкой жидкости:

а) F_тр = 6 πr²η ; б) F_тр = 6 πrη ²; в) F_тр = 6 πrη ; г) F_тр = 6 πrη/ .

16. В методе Стокса по определению коэффициента вязкости жидкости уравнение движения шарика записывается на основании:

а) закона Архимеда; б) второго закона Ньютона;

в) уравнения Ньютона для течения жидкости; г) первого закона Ньютона;

17. Укажите векторную диаграмму сил, действующих на шарик, в методе Стокса по определению коэффициента вязкости:

а б в г

18. Укажите, каким методом в медицине определяют коэффициент вязкости:

а) метод Стокса; б) метод капилляроскопии;
в) метод отрыва кольца; г) метод вискозиметрии.

19. Критическое число Рейнольдса определяет:

а) условия изменения вязкости жидкости;

б) условия изменения объемной скорости течения жидкости;

в) Условия изменения линейной скорости течения жидкости;

г) условия перехода от ламинарного течения жидкости к турбулентному.

20. Выберите правильное утверждение:

а) кровь является идеальной жидкостью;

б) кровь является ньютоновской жидкостью;

в) кровь является неньютоновской жидкостью.

Лабораторная работа №4

ИЗУЧЕНИЕ ДЕЙСТВИЯ УЛЬТРАВЫСОКОЧАСТОТНОГО (УВЧ) ЭЛЕКТРИЧЕСКОГО ПОЛЯ НА ВЕЩЕСТВО

Цель работы. Изучить механизм лечебного действия полей УВЧ на модели тканевых структур человека. Ознакомить студентов с аппаратом УВЧ-терапии и научить их работать с ним.

Актуальность. Ультравысокочастотные электрические поля являются самым мощным противовоспалительным средством из всех классических физиотерапевтических технологий. Однако врач должен быть полностью осведомлен обо всех нюансах механизма действия УВЧ-полей и об опасностях негативных последствий при назначении данного метода физиотерапевтического лечения.

Приборы и принадлежности: аппарат УВЧ-терапии, две пробирки (с электролитом и диэлектриком), неоновая лампочка.

Теоретическая часть

Классификационные диапазоны переменного электрического поля, используемого в физиотерапевтических процедурах и диагностике:

Инфразвуковая частота- 0,3-4,5 Гц.
Низкая частота- 4,5-20 Гц.
Звуковая частота- 20 Гц- 20 КГц.
Ультразвуковая частота (УЗЧ)- 20-200 КГц.
Высокая частота (ВЧ)- 0,2-30 МГц.
Ультравысокая частота (УВЧ)- 30-300 МГц.
Сверхвысокие частоты (СВЧ)- свыше 300 МГц:

Дециметровый диапазон- 460±4,6 МГц;
Сантиметровый диапазон- 2375 МГц.

8. Крайне высокая частота (КВЧ) – миллиметровый диапазон – 40–60 ГГц.

Как следует из классификации диапазонов, к электромагнитным волнам УВЧ относят колебания частотой от 30 МГц до 300 МГц и длиной волны от 10 до1 м. Однако в аппаратах УВЧ-терапии используются две фиксированные частоты – 40.68 МГц (советская техника в наше время не производится; соответственно длина волны – 7,37 м) и 27,12 МГц (длина волны – 11,05 м в технике западных производителей).

Лечебным фактором УВЧ-воздействий является электрическое поле (э.п.). Оно формируется между электродами (конденсаторные пластины), которые подключаются к аппарату через изолированные гибкие кабели- фидеры. Силовые линии э.п. УВЧ идут от одной пластины к другой, пронизывая ткани тела пациента. Между пластинами и поверхностью тела имеется воздушный зазор или сухая фетровая прокладка, причем суммарный зазор не должен превышать 6 см. Важно помнить технологический принцип:

· для глубокого прогревания тканей указанный зазор устанавливается на большую величину;

· для прогревания поверхностных тканевых структур устанавливаться зазор меньшей величины.

Необходимо также помнить, что э.п. УВЧ пронизывает ткани человека насквозь, т.е. проходит и через токопроводящие ткани и диэлектрики. В этом сквозном действии прослеживается некоторый недостаток УВЧ-терапии, т.е. невозможность фокусирования лечебного воздействия на конкретную глубину тканевой структуры.

Однако максимум поглощения энергии э.п. УВЧ в разных тканях неодинаков:

· Максимальное поглощение имеет место в тканях, бедных жидкостью, а именно: в нервной, костной и соединительной ткани, подкожной жировой клетчатке, сухожилиях и связках.

· В богатых водой тканях (кровь, лимфа, мышечная ткань) тепла образуется на порядок меньше.

Важно отметить, что тепловой компонент в УВЧ- терапии не является определяющим и ощутимо проявляется лишь при выраженном нарастании интенсивности УВЧ- колебаний. В физиотерапевтическом воздействии э.п. УВЧ на ткани выделяют два механизменных компонента:

осцилляторный или физико-химический компонент, называемый еще током смещения;
ток проводимости – линейно-поступательные перемещения зарядов.

Действительно, из-за большой длины электромагнитных волн УВЧ-диапазона и сквозного проникновения э.п. УВЧ через ткани (их емкостное сопротивлениена этих высоких частотах значительно меньше, чем на низких) э.п. УВЧ воздействует не только на клеточные мембраны, но и на субклеточные структуры.

Макромолекулы (прежде всего белки) в вихревом поле УВЧ совершают колебательные и вращательные смещения - это и есть нетепловой осцилляторный или физико-химический компонент (т.е. ток смещения). В терапевтическом плане он является ведущим, и на него приходится до 85% энергопревращений.

Высокочастотная поляризация тканей током смещения изменяет прежде всего физико-химические свойства мембран.

Однако в вязкой среде этот ток смещения макромолекул из-за значительных сил трения может сопровождаться значительным преобразованием энергии УВЧ электрического поля в тепловую. Теплообразование при таких процедурах может ощутимо превышать метаболическое теплообразование. А плохое кровоснабжение и обедненность водой указанных выше тканей делают их теплоотдачу неэффективной. Именно поэтому в физиотерапевтических технологиях существуют приемы, ослабляющие тепловой компонент и усиливающие осцилляторно-химическое воздействие э.п. УВЧ на ткани.

Для усиления «осцилляторного» эффекта при УВЧ–терапии используют импульсный режим воздействия электрическим полем, при котором кратковременные (микросекунды) импульсы поля достаточно высокой напряженности разделены в тысячи раз более длительными паузами. В этом случае сохраняется необходимое осцилляторное действие, а тепловой эффект снижается до ничтожной величины. Для УВЧ–терапии в импульсном режиме применяются особые аппараты.

В диэлектрике под действием электрического поля происходит ориентационная и структурная поляризация молекул. Вращательные колебания поляризованных молекул под действием переменного высокочастотного поля сопровождаются потерями энергии на преодоление взаимодействия между молекулами, которое удерживает их в равновесном положении. Эти потери, называемые диэлектрическими, зависят от природы диэлектрика.

Низкомолярные ионы при их механическом линейно-поступательном движении в вязкой среде также обеспечивают продуцирование тепла - это так называемый ток проводимости. Конечно, из-за малой массы ионов относительно белковых молекул теплопродукция при токе проводимости на порядок меньше, чем при токе смещения.

За счет возникающего под действием высокочастотного электрического поля тока проводимости происходит нагрев электролитов.

Тепловые эффекты УВЧ – терапии. Тепловой прогрев тканей вызывает в них стойкую, длительную и глубокую гиперемию:

· усиливается микроциркуляция в тканях (диаметр капилляров возрастает в 3–10 раз);

· увеличивается скорость кровотока в крупных сосудах;

· ускоряется местная лифмодинамика;

· повышается проницаемость биомембран.

Лечебные эффекты УВЧ-терапии:

· противовоспалительный;

· экскреторный (выработка и выделение железистыми клетками экскретов и

инкретов);

· сосудорасширяющий;

· миорелаксирующий (понижение тонуса скелетных и гладких мышц и их расслабление);

· иммуномодулирующий (изменение уровня активности местного и общего иммунитета);

· трофический (повышение обменных процессов, энергетического и кислородного обеспечения и активное удаление шлаков).